信号的采样与重建

第一问

要求

①固定采样频率500 kHz，分别对100 kHz、250 kHz、400 kHz的正弦波信号（幅度，相位自定义）进行采样和重建，分析比较原信号与重建信号的波形；

程序设计

clear
%参数设定
f1 = 100000;%信号频率
fs = 500000;%采样频率
dt = 1/fs; % 采样间隔，采样间隔可以理解为采样信号的周期，周期 = 1/频率
Tf = 1/f1; %  一个信号周期的时间

%可得参数
t = linspace(0,20*Tf,1000*20); % 原信号每个周期内的点数为1000个点
f_ori = cos(2 * pi * f1 * t) ;
%figure(1);
subplot(221);
plot(t, f_ori);title(strcat(num2str(f1/1000),'kHz原始信号'));xlabel('t/s');

%采样
t2  = 0:dt:t(end); % 整个信号时间范围内采样
f_sam =  cos(2 * pi * f1 * t2) ;
%figure(2);
subplot(222);
stem(t2, f_sam,'.');title('采样信号(500kHz采样率)');xlabel('t/s');

%fft变换
f_true=t2*fs/length(t2);
k=fft(f_sam,length(t2));
%figure(3);
subplot(223);
stem(f_true*fs/1e3,abs(k),'.');title('采样信号傅里叶变换');xlabel('kHz');

%恢复
y = [];
for i = 1 : length(t)
    x = t(i);
    h = sinc((x - t2).*fs);
    g = dot(f_sam, h);%向量相乘
    y = [y,g];
end
subplot(224);
%figure(4);
plot(t, y);title('恢复信号');xlabel('t/s');

实验结果

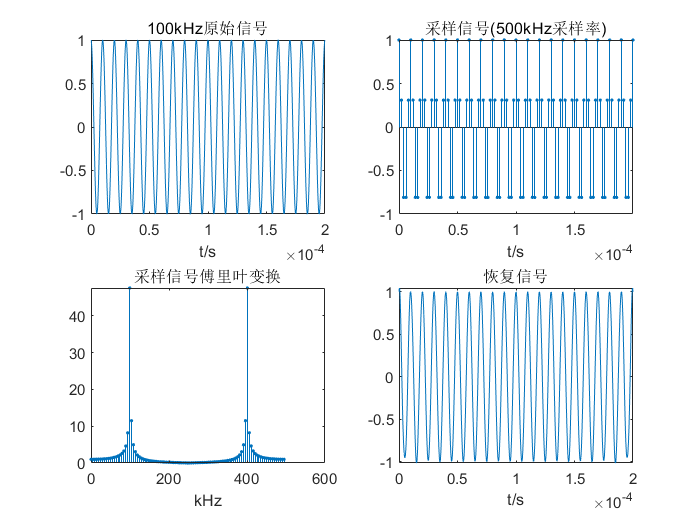
• 100kHz原始信号

  

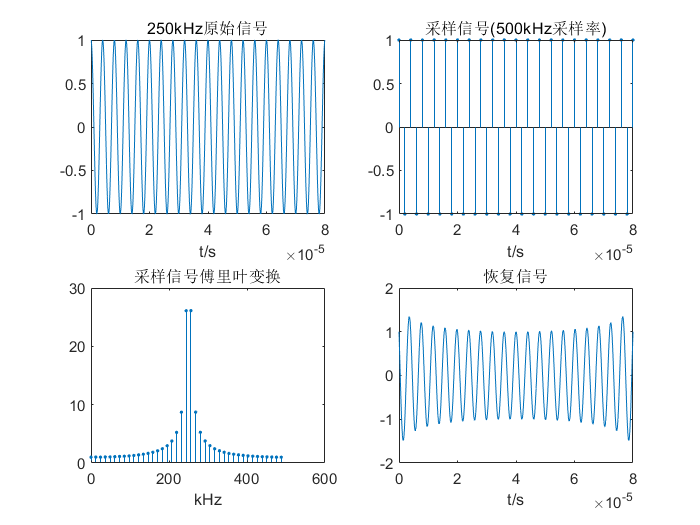
• 250kHz原始信号

  

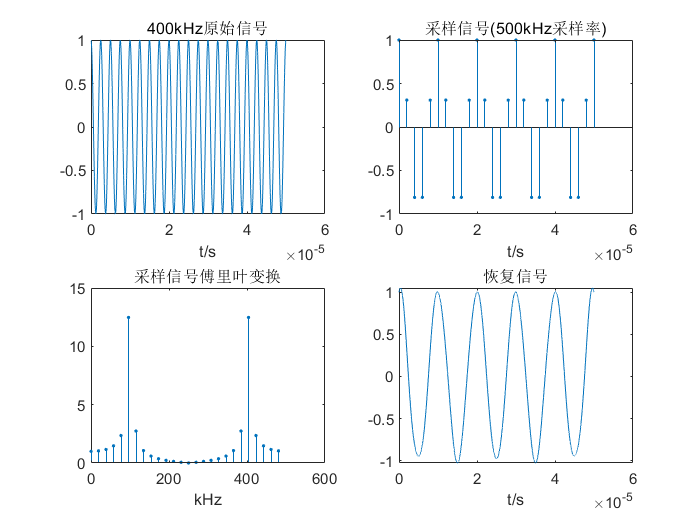
• 400kHz原始信号

  

分析总结

• 从上述图像中可以看出，当固定采样频率500kHz时，对于100kHz的信号采样并进行傅里叶变换后可以看出幅频特性较为准确，因为满足奈奎斯特采样定律，采样频率大于原始信号频率的两倍以上，处于过采样状态。当使用上述采样率采集250kHz的信号时出现了幅值一定的失真，此时处于临界采样状态。当使用上述采样率采集400kHz的信号时出现了幅值和频率的失真，此时处于欠采样状态。
• 上述程序设计中使用dot函数，具有一定创新性。

第二问

要求

②采集一段音频信号，分别用欠采样、临界采样和过采样对信号进行重采样，并重建原音频信号，分析比较重建信号与原信号的差别。

程序设计

clear
%声音信号的采样
[x,Fs] = audioread('oba.mp3');
x=x(:,1);%由于x是双声道，所以取它的左声道
x = resample(x,13000,Fs) ; %重新采样
x=x.';
Fs=13000;
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
%figure(1);
subplot(321);
plot(time,x);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
%figure(2);
subplot(322);
plot(f_true*Fs/1e3,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%对原始信号进行采样
fs=Fs/2; %新的采样率
y = resample(x,fs,Fs) ; %从x中第一个元素开始采样(奇采样)
n_sam=length(y);%获取y的采样点数
dt_sam=1/fs;%求采样间隔
time_sam=(0:n_sam-1)*dt_sam;%新的采样时间点
%figure(3);
subplot(323);
plot(time_sam,y);
title('过采样信号时域波形')
xlabel('时间/s');

%采样信号fft变换
f_true_sam=time_sam*Fs/length(time_sam);
k=fft(y,length(time_sam));
%figure(4);
subplot(324);
plot(f_true_sam*fs/1e3,abs(k));title('过采样信号傅里叶变换');xlabel('kHz');

%重建信号
z = [];
for i = 1 : length(x)
    m = time(i);
    h = sinc((m - time_sam).*fs);
    g=0;
    for j = 1:1:length(y)
        s=y(j)*h(j);
        g=g+s;
    end
    %g = dot(y, h);%向量相乘
    z = [z,g];
end
%figure(5);
subplot(325);
plot(time, z);title('重建声音信号');xlabel('t/s');

%重建信号fft变换
f_true=time*Fs/length(time);
k=fft(z,length(time));
%figure(6);
subplot(326);
plot(f_true*Fs/1e3,abs(k));title('重建声音信号傅里叶变换');xlabel('kHz');

%试听和写入信号
 sound(z,Fs);
 audiowrite('over_sampling.wav',z,Fs);

实验结果

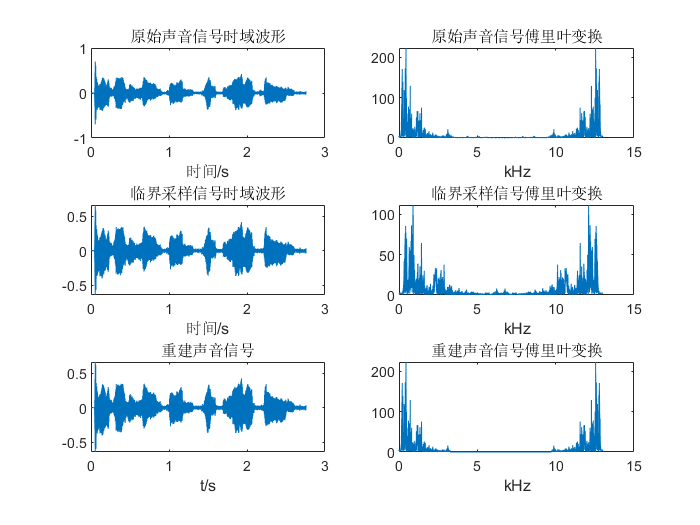
• 临界采样

  

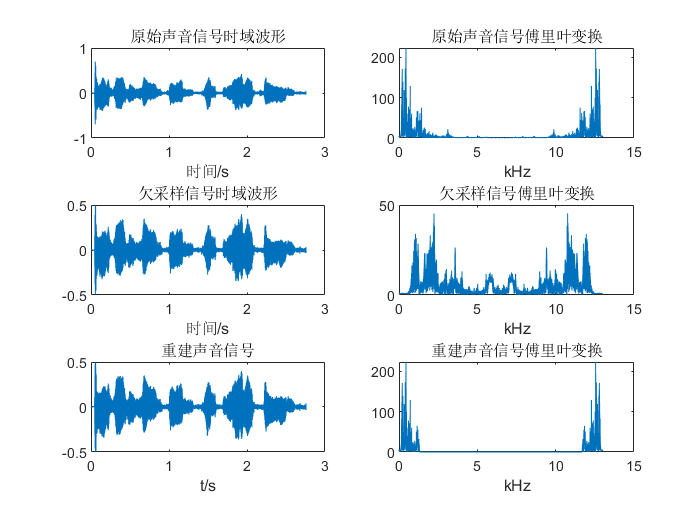
• 欠采样

  

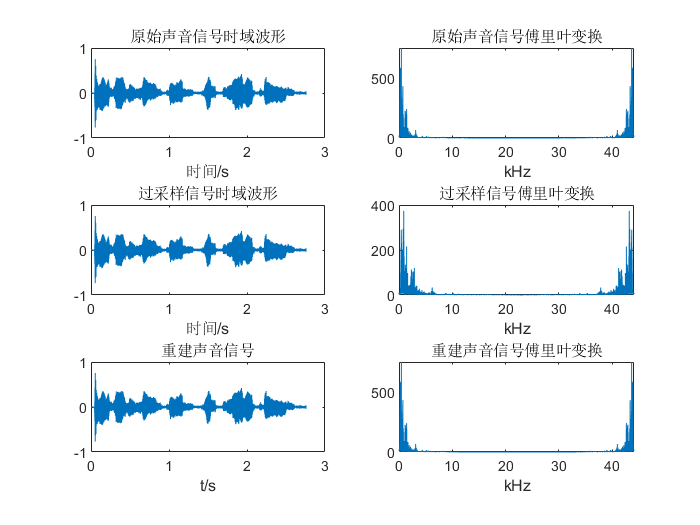
• 过采样

  

分析总结

• 首先对音频信号进行快速傅里叶变换和查阅人类发出声音的频率范围确定最高频率，此处取6.5kHz采样率作为临界采样率，由此可以得知低于6.5kHz采样率为欠采样，高于6.5kHz采样率为过采样。
• 按照上述分析理论进行设计并测试，对比其傅里叶变换频谱图看出符合上述理论，对比试听恢复的声音信号（见附件），可以听到临界采样恢复的声音信号和过采样恢复的声音信号与原信号差别不大，而欠采样的信号与原信号相比有较大失真，与奈奎斯特采样定理的理论相符合。