信号的时域处理

第一问

要求

① 选择子作业１中的音频信号，自行给定滤波器的系统函数，采用差分方程方法对音频信号进行滤波处理，比较滤波前后信号的波形和回放的效果。

实验原理

• 对于直接I型的IIR滤波器(无限长单位冲激响应滤波器)的系统函数为：

$$H(z)=\frac{Y(z)}{X(z)}=\frac{\sum _{k=0}^{M}b_{k}z^{-k}}{1-\sum _{k=1}^{N}a_{k}z^{-k}}$$

• 其对应的差分方程为：

$$y(n)=\sum _{k=1}^{N}a_{k}y(n-k)+\sum _{k=0}^{M}b_{k}x(n-k)$$

• 由此，我们只需要求出对应的差分方程系数就能够确定一个IIR滤波器。

巴特沃斯滤波器的设计

• 比较经典的IIR滤波器有巴特沃斯滤波器，我们可以根据我们所需要设计的需求来确定通带截止频率和阻带截止频率以及通带最大衰减分贝和阻带最小衰减分贝，运用Matlab完善的函数运算功能就能够确定出巴特沃斯滤波器的对应的差分方程系数。

程序设计

clear;

%声音信号的采样
[x,Fs] = audioread('Carmen_overture_noisy_8k_9.5k.wav');
x=x.';%转置
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
subplot(221);
plot(time,x);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(222);
plot(l,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%巴特沃斯滤波器设计
wp=2*7760/Fs;%通带截止频率（数字滤波器作归一化变换）
ws=2*8000/Fs;%阻带截止频率（数字滤波器作归一化变换）
Rp=2;%通带最大衰减2dB
As=30;%阻带最小衰减30dB
[N,wc]=buttord(wp,ws,Rp,As);%求滤波器的阶数N与3dB截止频率wc
[b,a]=butter(N,wc);%得到差分方程系数
y=filter(b,a,x);%滤波
subplot(223);
plot(time,y);
title('直接法滤波后声音信号时域波形')
xlabel('时间/s');

%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(224);
plot(l,abs(k));title('直接法滤波后声音信号傅里叶变换');xlabel('kHz');

%绘制归一化滤波器参数
figure(2);
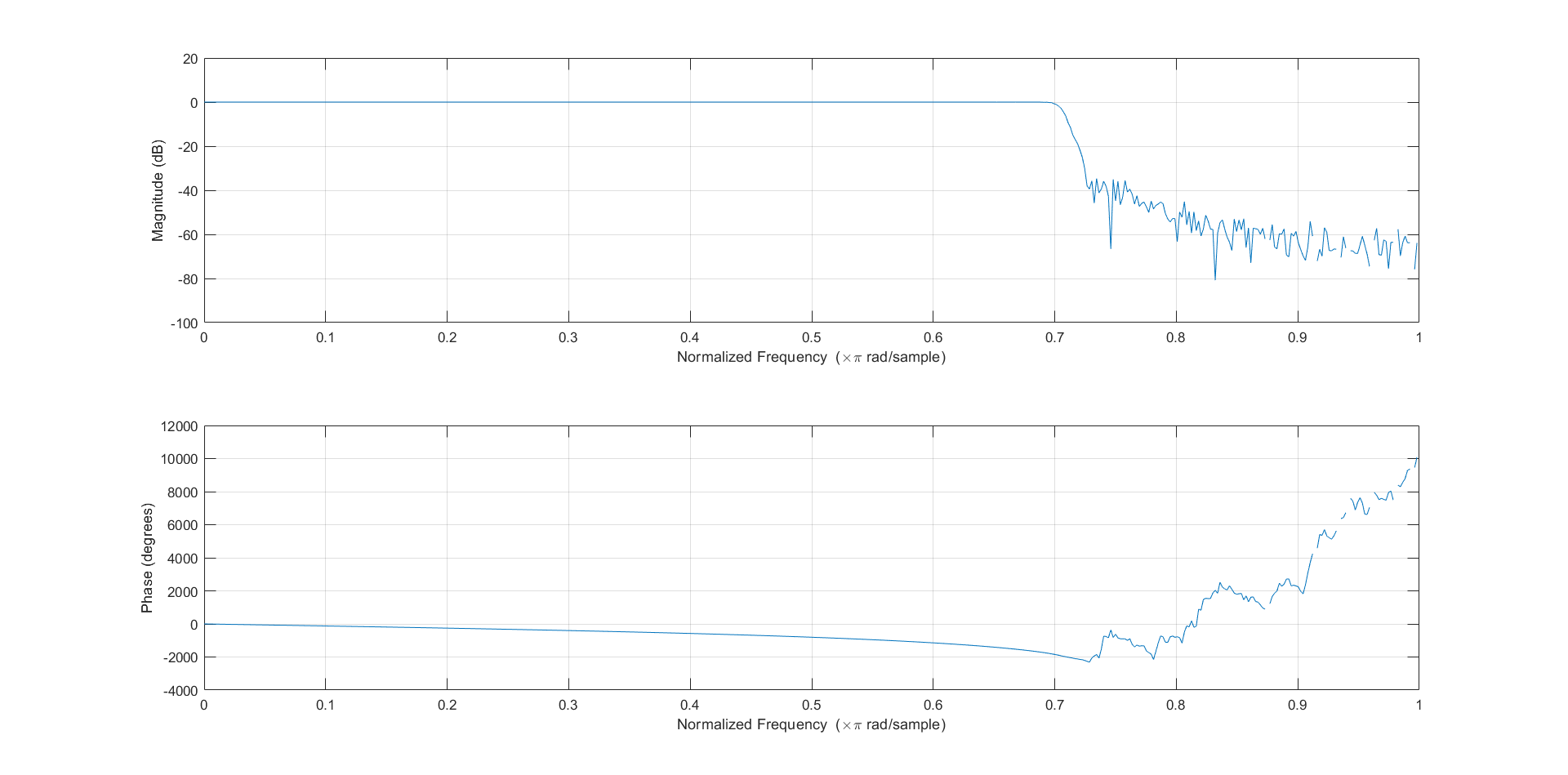
freqz(b,a);

%写入和试听音频
audiowrite('direct.wav',y,Fs);

实验结果

• 巴特沃斯滤波器归一化频率幅频响应和相频响应

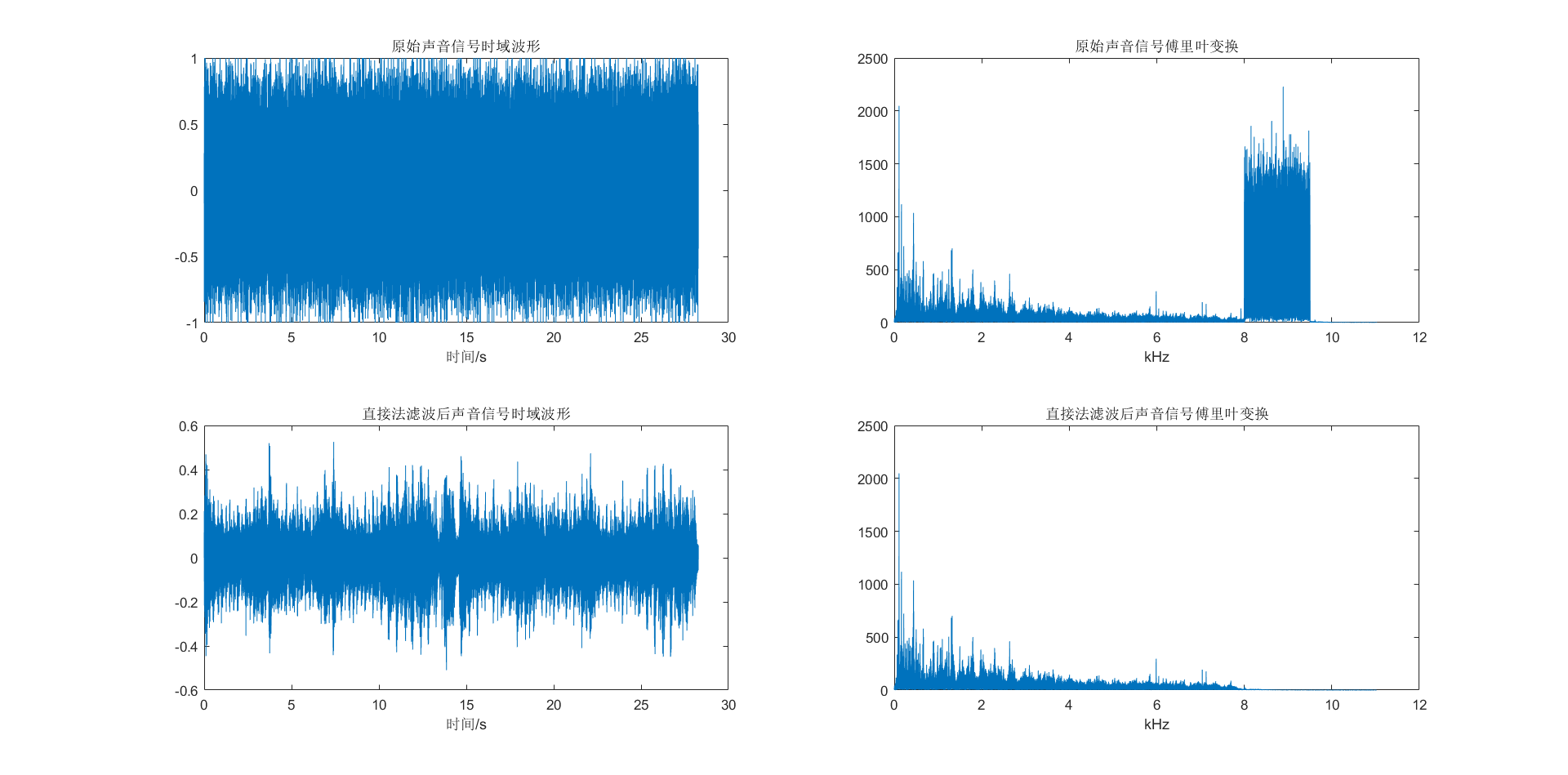
• 巴特沃斯滤波器滤波效果

分析总结

• 首先对原始音频信号进行快速傅里叶变换观察其频谱，发现在8kHz-9.5kHz有高频噪声信号。因此，滤波器理论截止频率应该在8kHz。查阅资料，对于差分方程法，我们选择IIR型中的巴特沃斯滤波器。经过多次测试，发现设置通带截止频率为7.76kHz，阻带截止频率为8kHz，通带最大衰减2dB，阻带最小衰减30dB。通过运算后得到滤波器系统函数的分子、分母多项式系数向量b和向量a，即为差分方程的系数。根据系统函数直接运算得到滤波效果如上图所示，试听生成的音频发现高频噪声已经滤去。

第二问

要求

② 选择子作业１中的音频信号，自行给定滤波器的系统函数，采用时域线性卷积对音频信号进行滤波处理，比较滤波前后信号的波形和回放的效果。

实验原理

• 对于FIR数字滤波器（有限长单位冲激响应滤波器），由于

$$H(z)=\sum _{k=0}^{M}b_{k}z^{-k}=\sum _{k=0}^{M}h\left[ k \right] z^{-k}$$

• 因此设计FIR数字滤波器时，我们只需要求出 $h[k]$，即滤波器的单位冲激响应，与音频信号进行卷积后得到滤除高频噪声的音频信号。

程序设计

clear;

%声音信号的采样
[x,Fs] = audioread('Carmen_overture_noisy_8k_9.5k.wav');
x=x.';
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
subplot(221);
plot(time,x);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半;
subplot(222);
plot(l,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%fir（默认汉宁窗）滤波器设计
h=fir1(3000,7.99e3*2/22.05e3);
y = conv(x,h);%卷积运算
y(:,length(x)+1:length(y)) = [];%将卷积后信号的长度变换为原信号长度
subplot(223);
plot(time,y);
title('卷积法滤波后声音信号时域波形')
xlabel('时间/s');

%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(224);
plot(l,abs(k));title('卷积法滤波后声音信号傅里叶变换');xlabel('kHz');

%试听和写入信号
 audiowrite('fir_conv.wav',y,Fs);
 
figure(2);
stem(h,'.');
title('FIR单位冲激响应')
axis([1460 1540 -0.3 0.8]);

实验结果

• Hamming窗函数(单位冲激响应)

• Hamming窗函数滤波效果

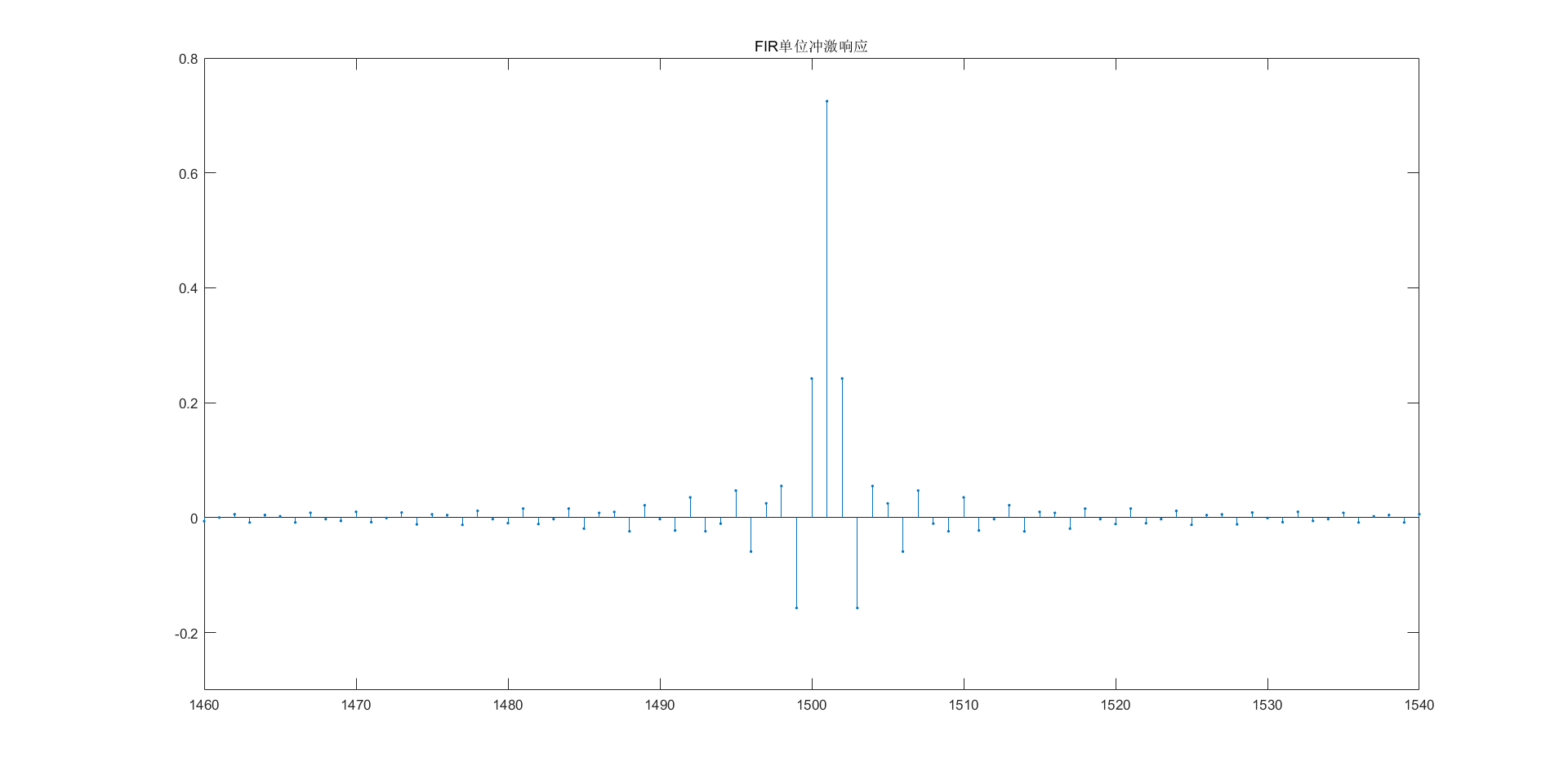
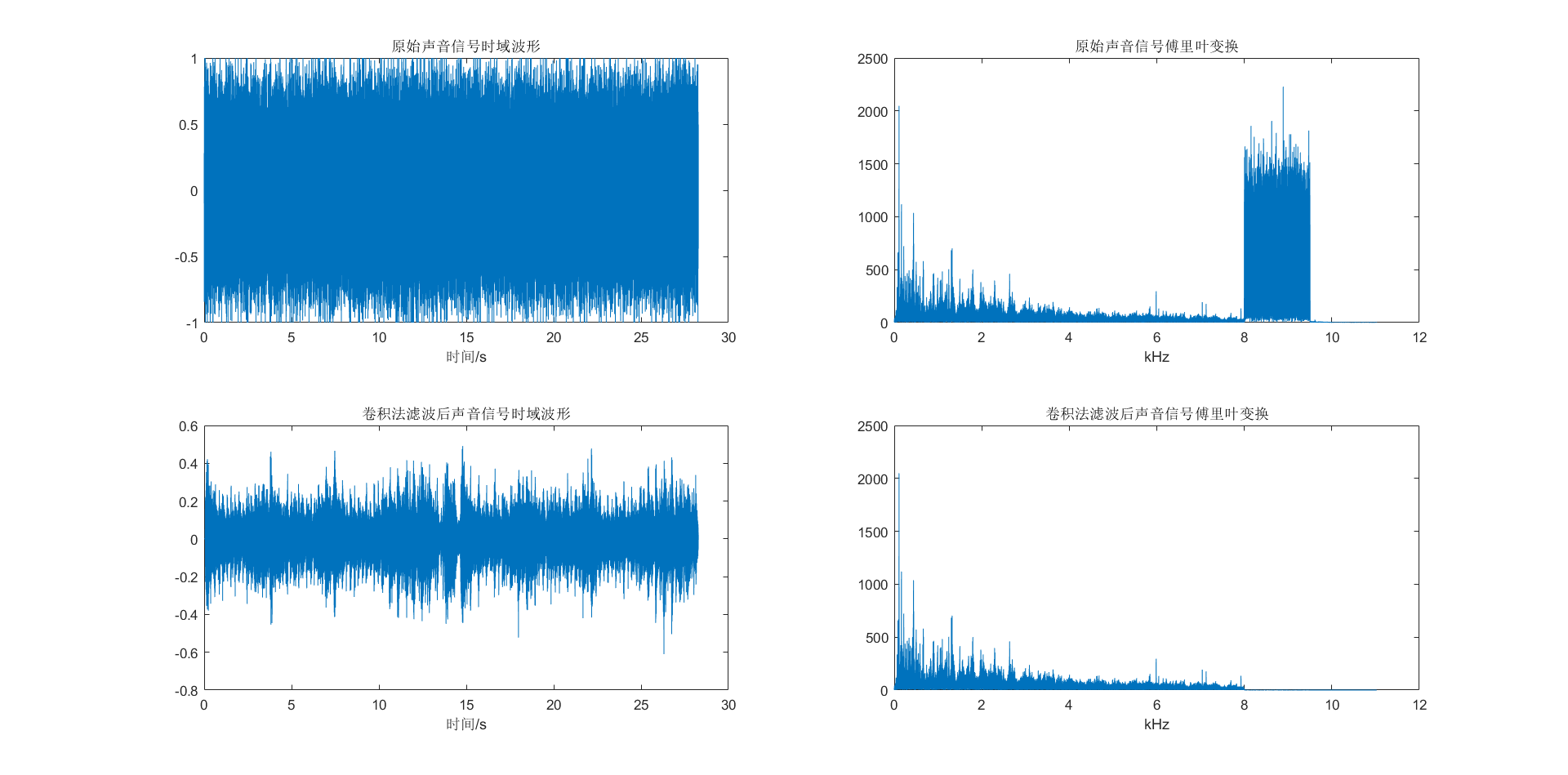
分析总结

• 首先对原始音频信号进行快速傅里叶变换观察其频谱，发现在8kHz-9.5kHz有高频噪声信号。因此，滤波器理论截止频率应该在8kHz。查阅资料，对于时域卷积法，我们选择FIR型中的Hamming窗。经过多次测试，发现设置3000阶的幅值3dB衰减对应频率在7.99kHz时效果较好。通过运算后得到滤波器的部分单位冲激响应如上图所示。根据单位冲激响应直接和时域波形进行卷积运算得到滤波效果如上图所示，试听生成的音频发现高频噪声已经滤去。