快速卷积实现滤波

要求

​ 选择子作业１中的音频信号，自行给定滤波器的单位取样响应，采用快速卷积实现对音频信号的滤波，比较滤波前后信号的波形和回放的效果。

滤波器设计原理

• 对于FIR数字滤波器（有限长单位冲激响应滤波器），由于

$$H(z)=\sum _{k=0}^{M}b_{k}z^{-k}=\sum _{k=0}^{M}h\left[ k \right] z^{-k}$$

• 因此设计FIR数字滤波器时，我们只需要求出 $h[k]$，即滤波器的单位冲激响应，与音频信号进行卷积后得到滤除高频噪声的音频信号。

快速卷积设计原理

通过数字信号处理课程的学习，我们知道对信号在时域上卷积，再对卷积后的结果作傅里叶变换，就是在频域上乘积。利用这个定理，我们将 h(n) 和 x(n) 通过快速傅里叶变换得到频域信号 $H(\omega)$和$X(\omega)$，然后相乘得到$Y(\omega)$，最后将 $Y(\omega)$通过 IFFT 从频域变换为时域即可。流程图如下：

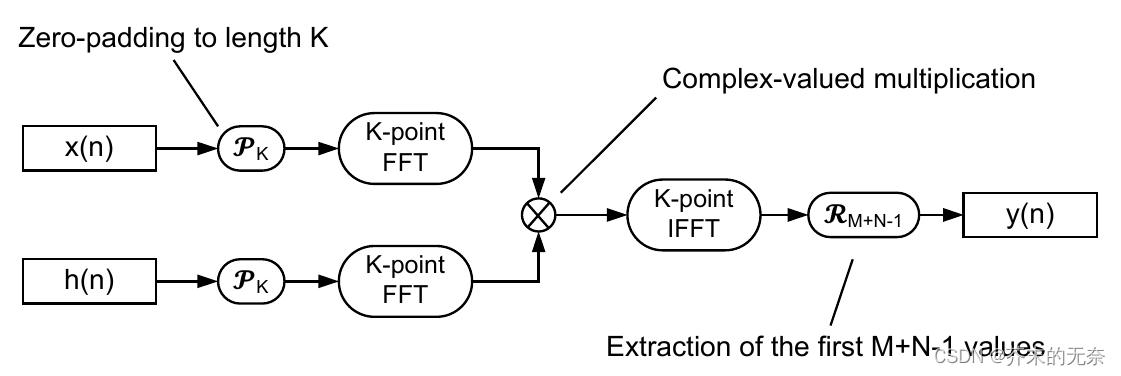
程序设计

clear;

%声音信号的采样
[x,Fs] = audioread('Carmen_overture_noisy_8k_9.5k.wav');
x=x.';
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
subplot(321);
plot(time,x);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半subplot(222);
subplot(322);
plot(l,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%fir（默认汉宁窗）滤波器设计
h=fir1(3000,7.99e3*2/22.05e3);

%快速卷积替代原matlab卷积函数
L=pow2(nextpow2(length(x)+length(h)-1));
xk=fft(x,L);
hk=fft(h,L);
yk=xk.*hk;
y=ifft(yk,L);

%y = conv(x,h);%卷积运算
y(:,length(x)+1:length(y)) = [];%将卷积后信号的长度变换为原信号长度
subplot(323);
plot(time,y);
title('快速卷积法滤波后声音信号时域波形')
xlabel('时间/s');

%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(324);
plot(l,abs(k));title('快速卷积法滤波后声音信号傅里叶变换');xlabel('kHz');

%与matlab原程序对比
y = conv(x,h);%卷积运算
y(:,length(x)+1:length(y)) = [];%将卷积后信号的长度变换为原信号长度
subplot(325);
plot(time,y);
title('卷积法滤波后声音信号时域波形')
xlabel('时间/s');

%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(326);
plot(l,abs(k));title('卷积法滤波后声音信号傅里叶变换');xlabel('kHz');

%试听和写入信号
audiowrite('fir_conv.wav',y,Fs);
 
figure(2);
stem(h,'.');
title('FIR单位冲激响应')
axis([1460 1540 -0.3 0.8]);

实验结果

• Hamming窗函数(单位冲激响应)

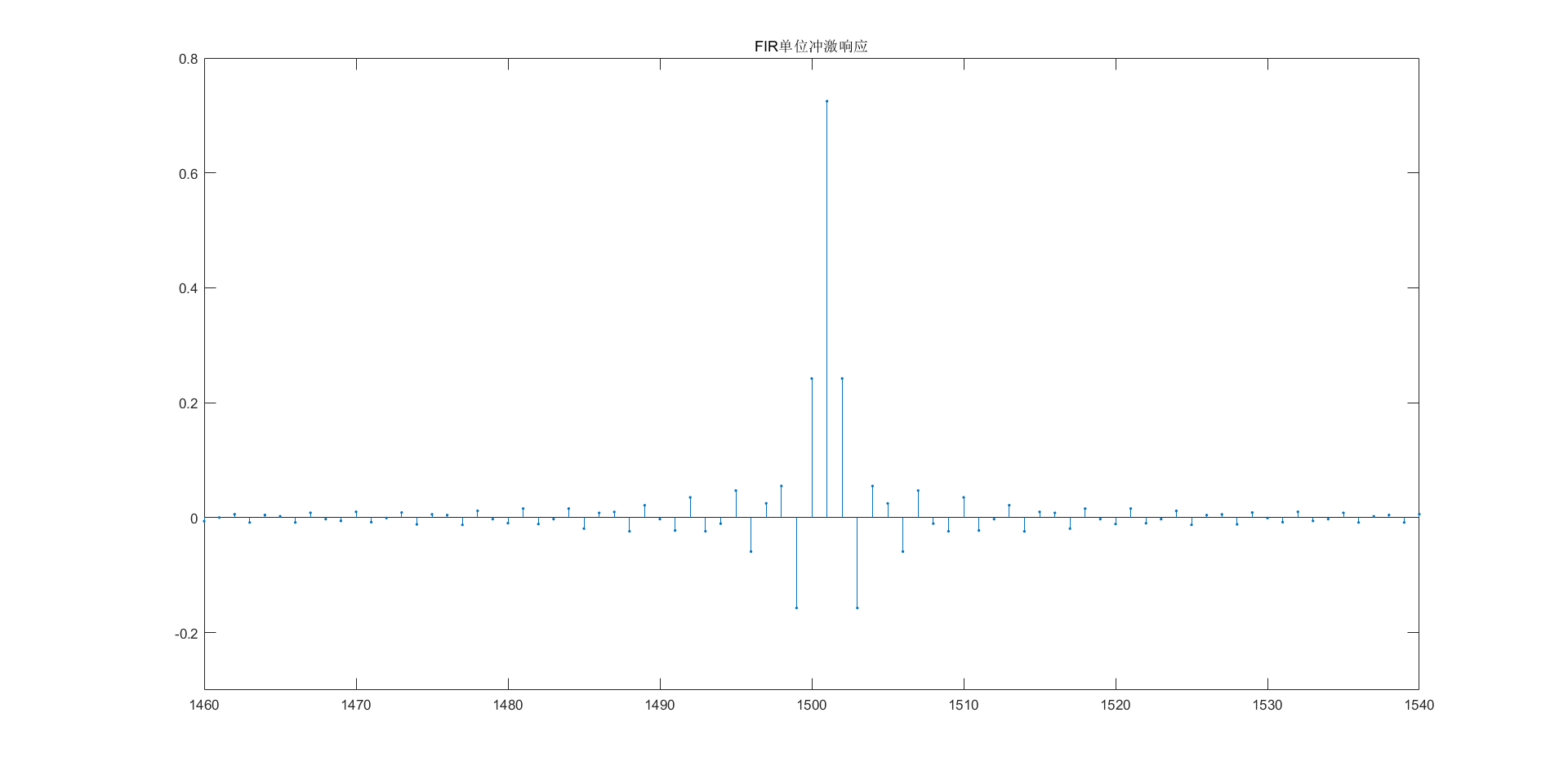
• 快速卷积和Matlab卷积函数滤波效果对比

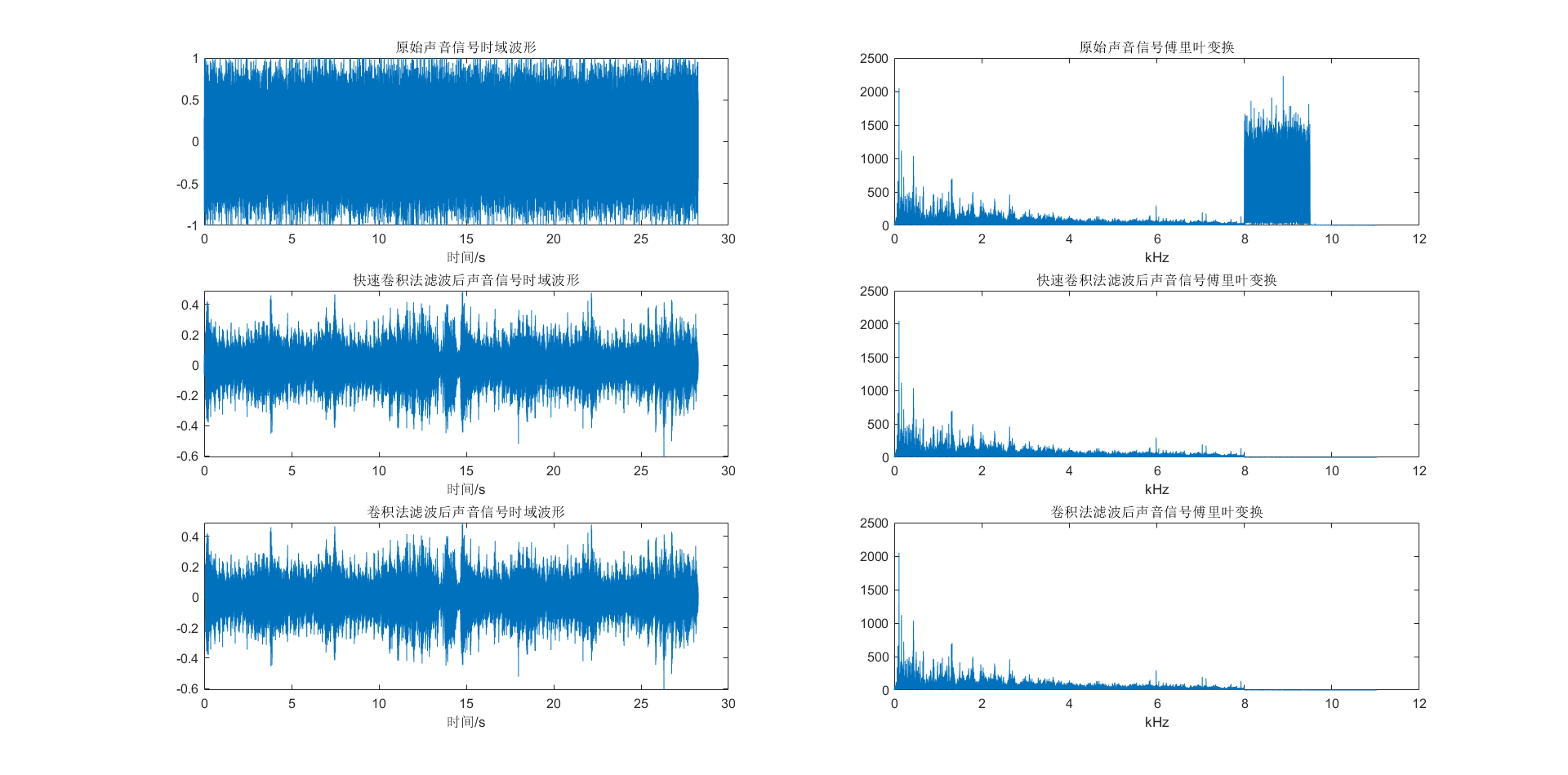
分析总结

• 根据信号的时域处理的实验得到的FIR型滤波器系数，我们只需要重新设计快速卷积函数替换原本在matlab的卷积函数即可。查阅相关资料我们可以了解到快速卷积的实现可以利用两次快速傅里叶变换将原始音频的采样序列和滤波器系数组成的序列变换为频域后相乘，得到其时域卷积下的频域序列，再利用快速傅里叶逆变换转换为时域即可。这个过程总共使用了三次快速傅里叶变换，从上述图片的结果可以看出，快速卷积和Matlab卷积函数实现的滤波效果基本一致。

数字信号处理教程推荐