数字滤波器设计

要求

​ 在子作业4的基础上，采用MATLAB的filterDesigner或fdatool工具箱，设计出相应的IIR滤波器和FIR滤波器。

音频加噪处理

​ 由于在子作业1中的音频较为纯净，没有过多噪声。为了方便数字滤波器性能指标的分析和数字滤波器的设计，需要对原有的音频进行加噪处理。本项目通过在音频的8.5kHz至10kHz中增加带限噪声，并在绘制出其时域波形和频域波形。

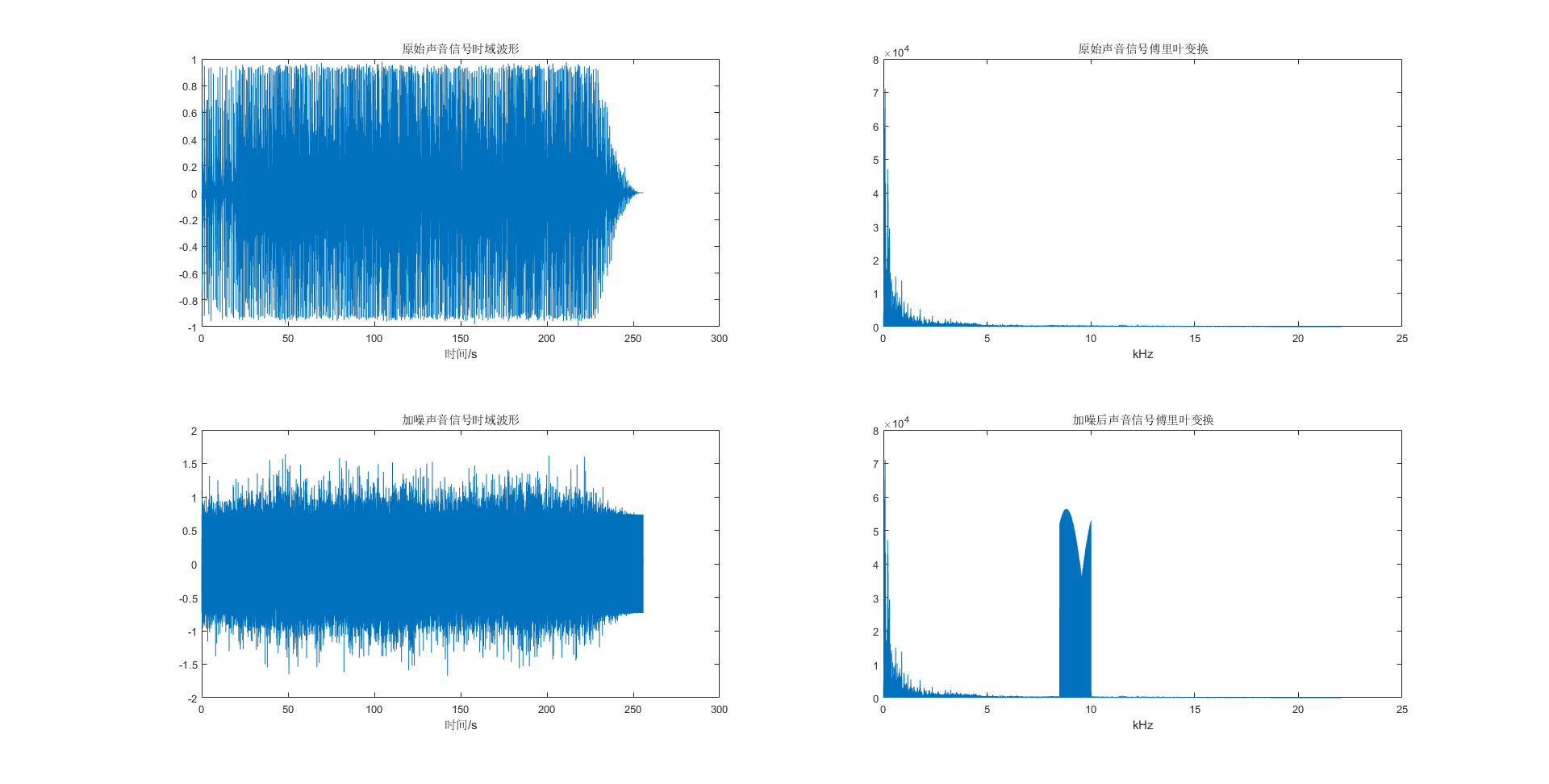
加噪程序设计

clear ;

%声音信号的采样
[x,Fs] = audioread('puppy love.mp3');
x=x(:,1);%由于x是双声道，所以取它的左声道
x=x.';%转置
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
subplot(221);
plot(time,x);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(222);
plot(l,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%加入带限噪声
noise=0;
for f=8500:20:10000
noise=noise+0.01*sin(2*pi*f*time);
end
xa=x+noise;
subplot(223);
plot(time,xa);
title('加噪声音信号时域波形')
xlabel('时间/s');

%加噪信号傅里叶变换
f_true=time*Fs/length(time);
k=fft(xa,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(224);
plot(l,abs(k));title('加噪后声音信号傅里叶变换');xlabel('kHz');

数字滤波器性能指标分析

假设数字滤波器的频率响应表示为：

$$H(e^{j \omega})=|H(e^{j \omega})|e^{j \beta(j \omega)}$$

根据下图中理想低通滤波器逼近的误差容限可以看出，频率响应有通带、过渡带、阻带三个范围。

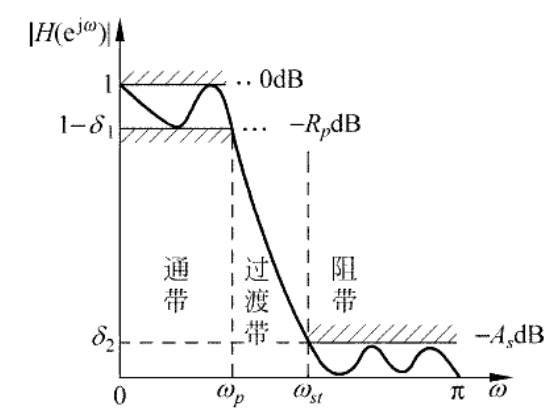
下图为不同滤波器的技术指标：

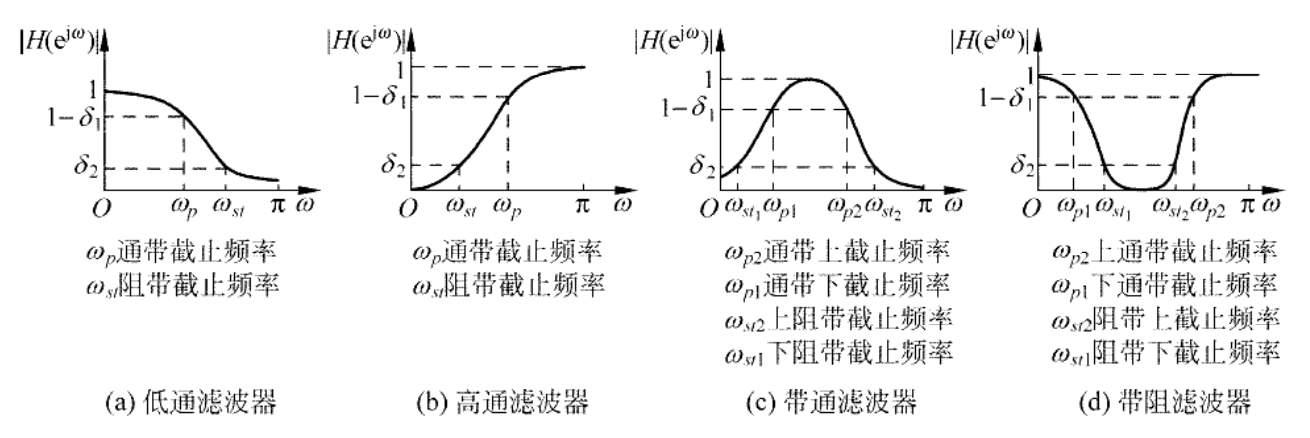
​ 因此我们对加噪后的音频频谱进行分析，可以确定出通带截止频率为8kHz，阻带截止频率为8.5kHz。通带最大允许衰减为1dB,阻带最小允许衰减为80dB。

Matlab数字滤波器设计

​ 经过上述分析得到数字滤波器的性能指标后，采用MATLAB的filterDesigner或fdatool工具箱，设计出相应的IIR滤波器和FIR滤波器。设计过程如下图所示：

• FIR滤波器设计(凯撒窗函数)

• IIR滤波器设计(切比雪夫II型)

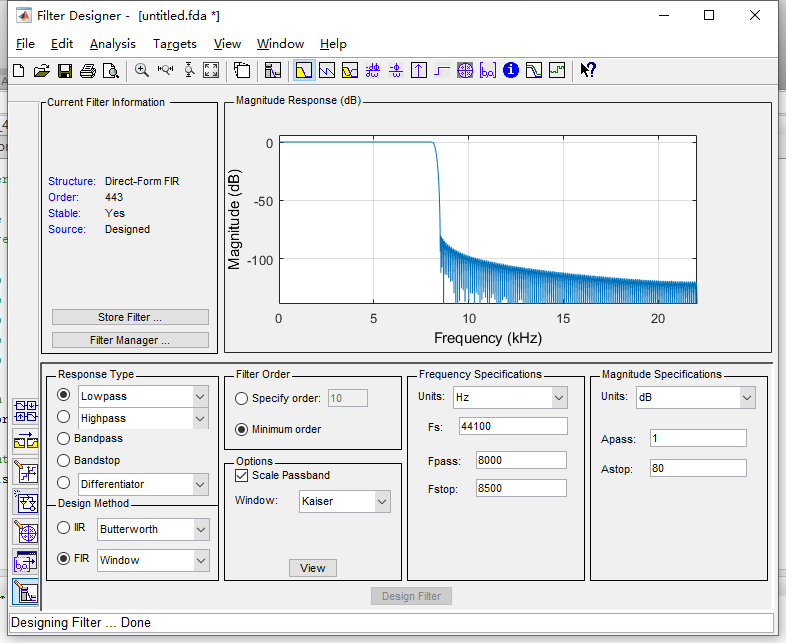
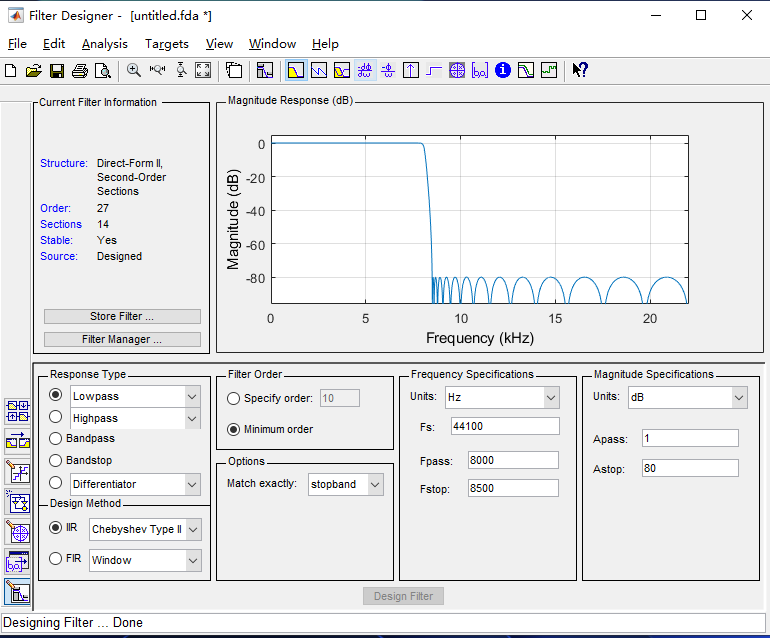
滤波程序设计

clear ;

%声音信号的采样
[x,Fs] = audioread('puppy love.mp3');
x=x(:,1);%由于x是双声道，所以取它的左声道
x=x.';%转置
n=length(x);%获取x的采样点数
dt=1/Fs;%求采样间隔
time=(0:n-1)*dt;%采样时间点
subplot(421);
plot(time,x);
%axis([0 300 -3 3]);
title('原始声音信号时域波形')
xlabel('时间/s');

%原始信号fft变换
f_true=time*Fs/length(time);
k=fft(x,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(422);
plot(l,abs(k));title('原始声音信号傅里叶变换');xlabel('kHz');

%加入带限噪声
noise=0;
for f=8500:20:10000
noise=noise+0.01*sin(2*pi*f*time);
end
xa=x+noise;
subplot(423);
plot(time,xa);
%axis([0 300 -3 3]);
title('加噪声音信号时域波形')
xlabel('时间/s');

%加噪信号傅里叶变换
f_true=time*Fs/length(time);
k=fft(xa,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(424);
plot(l,abs(k));title('加噪后声音信号傅里叶变换');xlabel('kHz');

%FIR滤波器(凯撒窗)设计
y = filter(my_fir,xa);  % 直接使用设计好的滤波器进行滤波，filter函数是滤波函数
subplot(425);
plot(time,y);
title('FIR滤波器(凯撒窗)滤波后声音信号时域波形')
xlabel('时间/s');


%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(426);
plot(l,abs(k));title('FIR滤波器(凯撒窗)滤波后声音信号傅里叶变换');xlabel('kHz');

%IIR滤波器(切比雪夫二型)设计
y1 = filter(my_iir,xa);  % 直接使用设计好的滤波器进行滤波，filter函数是滤波函数
subplot(427);
plot(time,y1);
title('IIR滤波器(切比雪夫二型)滤波后声音信号时域波形')
xlabel('时间/s');


%滤波后信号fft变换
f_true=time*Fs/length(time);
k=fft(y1,length(time));
k(:,ceil(length(k)/2):end) = [];%去掉快速傅里叶变换对称的一半
l=f_true*Fs/1e3;
l(:,ceil(length(l)/2):end) = [];%去掉快速傅里叶变换对称的一半
subplot(428);
plot(l,abs(k));title('IIR滤波器(切比雪夫二型)滤波后声音信号傅里叶变换');xlabel('kHz');

%sound(y,Fs)
%sound(xa,Fs)
%sound(x,Fs)
clear sound

分析总结

​ 通过上述分析实验可以看出加噪后的音频在经过采用MATLAB的filterDesigner或fdatool工具箱，设计出相应的IIR滤波器和FIR滤波器滤除后的频谱图中噪声信号已经完全滤除，时域波形也与原信号相似，在对滤波的音频试听后发现，噪声几乎已经完全听不见，滤波效果较好。滤波效果如下图所示：

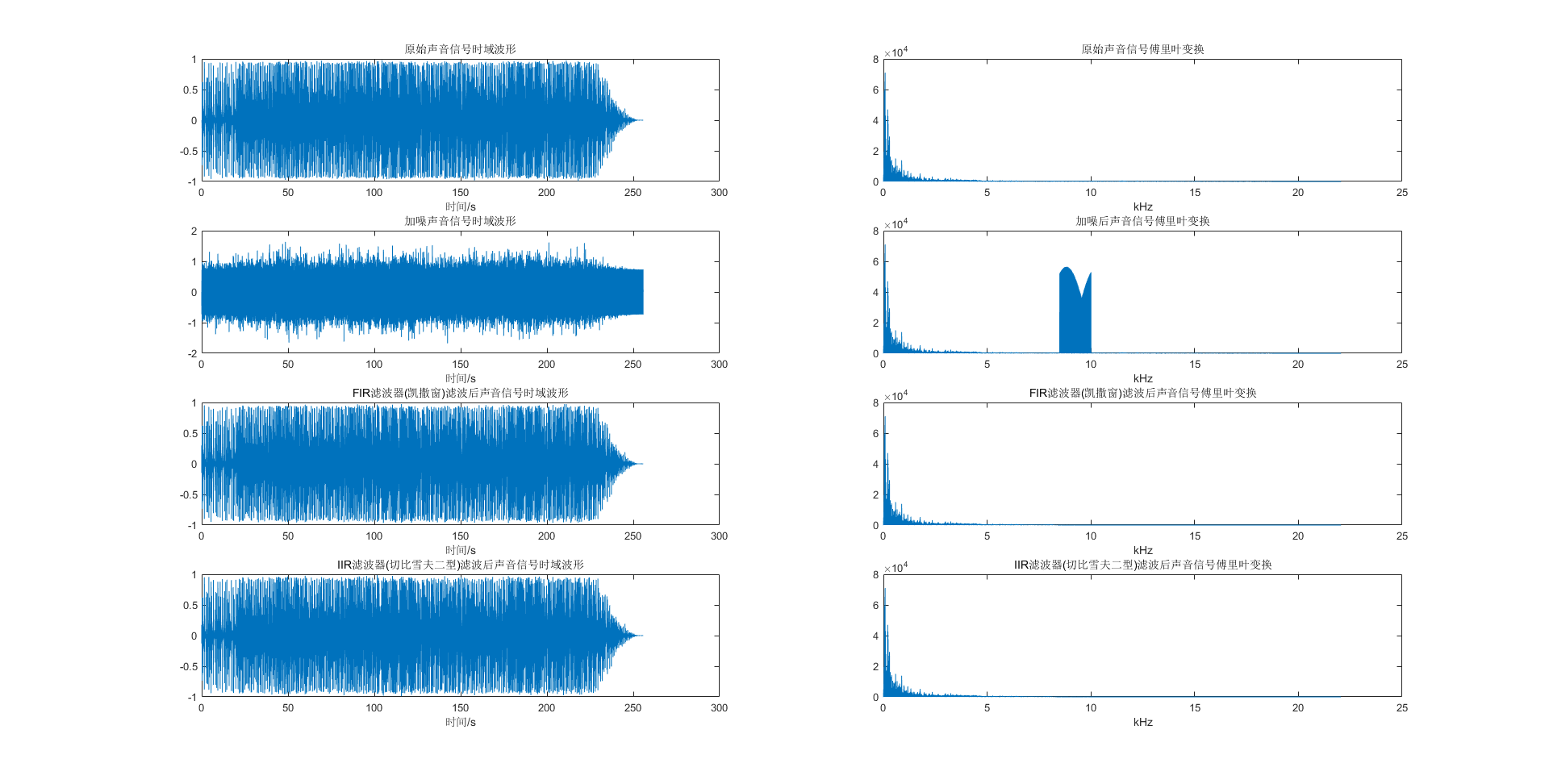
项目开源

点击🔗即可下载完整可运行项目： 项目下载