算法笔记之基础篇

算法笔记之基础篇

C/C++快速入门

头文件

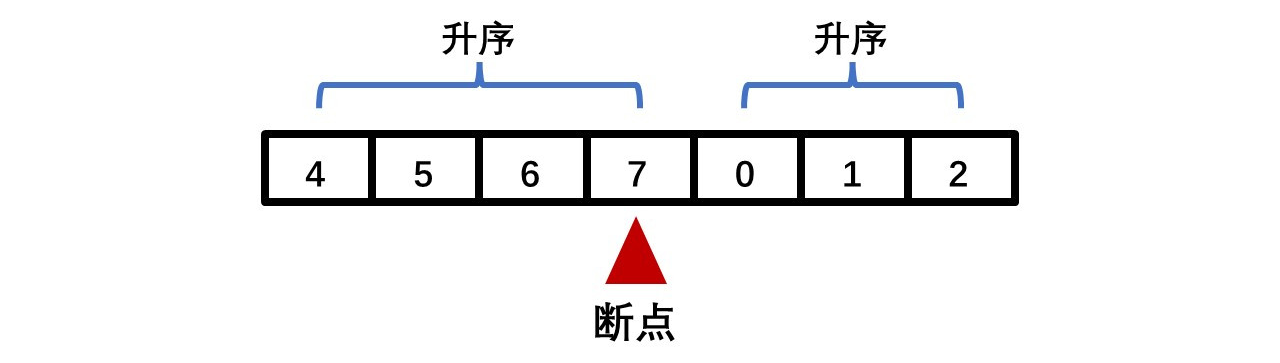
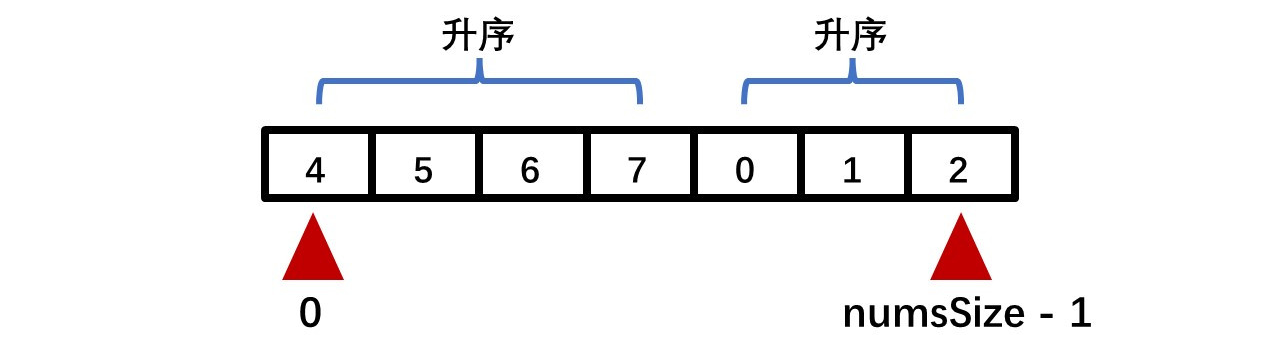
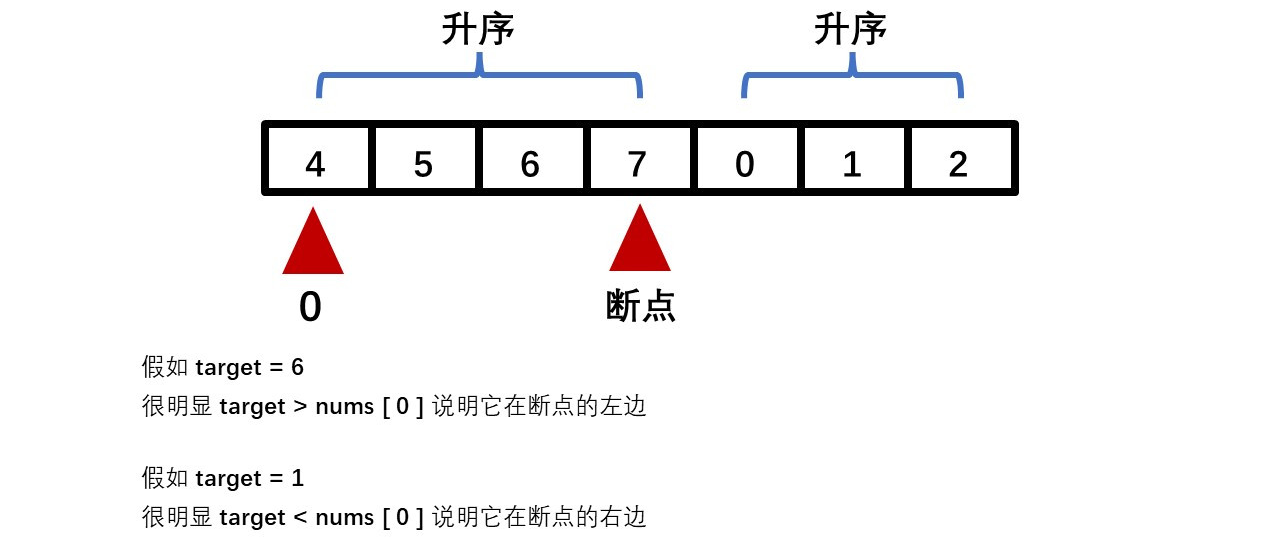
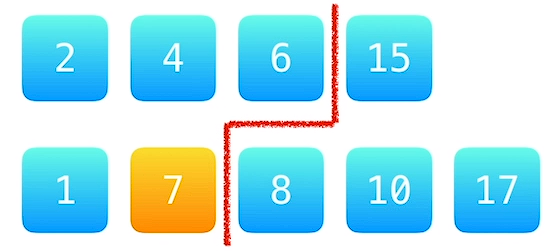
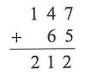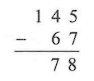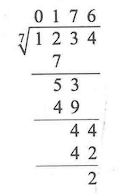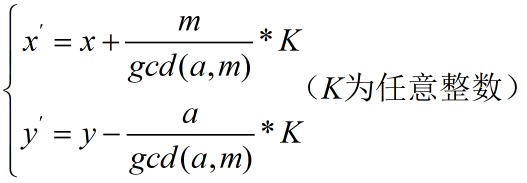  • 当我们忘记函数包含在哪个头文件下时或者头文件包含较多时，可以使用这个万能头文件来代替。但这个头文件也有缺点，最明显的是使用后编译时间太长。另外，由于 include＜bits/stdc++.h＞不是C++的标准头文件，所以会有少部分编译器不支持。因此建议使用标准头文件！

主函数

  • 主函数是一个程序的入口位置，整个程序从主函数开始执行，而且一个程序最多只能有一个主函数。

基本数据类型

变量的定义

  • 变量是在程序运行过程中其值可以改变的量，需要在定义之后才可以使用。

变量的类型

基本数据类型
  • 基本数据类型分为整型、浮点型、字符型和布尔型。

  • 注意在计算机系统中不管正数与负数的表示和存储都是以补码的形式。
  • 原码的表示为：第一位表示符号（0为正，1为负），其余位表示数值。
  • 反码的表示方法分为正数和负数两种：
    • 正数的反码等于原码本身。
    • 负数的反码是在其原码的基础上，符号位不变（即首位不变），其余各位按位取反。
  • 补码的表示方法同样分为正数和负数两种：
    • 正数的补码是其原码本身。
    • 负数的补码是在其原码的基础上，符号位不变，其余各位按位取反后加1（即在反码的基础上加1）。
整型(int)
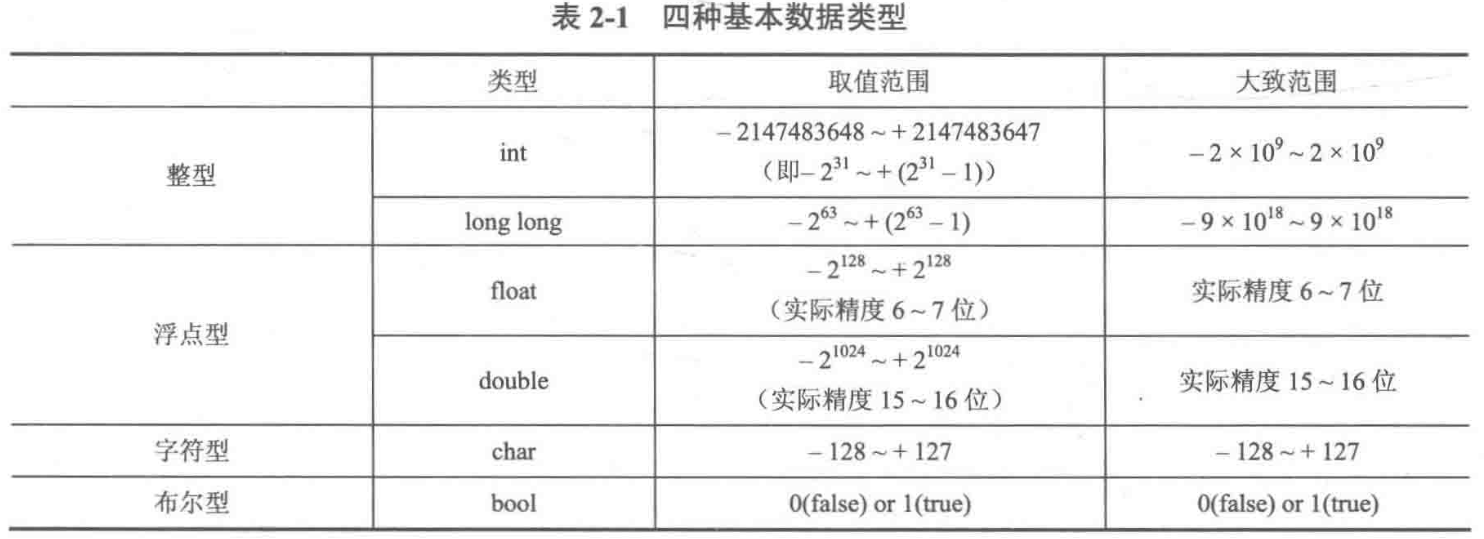
  • 对于整型int而言，一个整数占32bit，即4个Byte，一般绝对值在10910^9范围以内的整数都可以定义为int型。
长整型(long long)
  • 对于长整型long long而言，一个整数占64bit，即8个Byte，如果需要的整数取值范围超过2147483647(超过101010^{10})就需要使用长整型。
浮点型
  • %f是单精度浮点型(float)和双精度浮点型(double)的输出格式
  • 对于浮点型而言，一般不需要使用float，碰到浮点型都应该使用double来进行存储。
字符型
字符变量和字符常量
1
2
char c;
char c = 'e';
  • 从上面的程序中可以看出来，第一段的c被成为字符变量，对于带单引号的‘e’则被称为字符常量，而且必须是单个字符。
  • 小写字母比大写字母的ASCII码值大32。
  • %c是char型的输出格式。
转义字符
  • ASCII码中有一部分是控制字符，是不可显示的。
  • 比较常用的转义字符：

\n 表示换行

\0 表示空字符NULL，其ASCII码为0，要注意 \0 不是空格

字符串常量

字符串常量可以作为初值赋给字符串数组，并且使用%s的格式输出。

1
2
3
4
5
6
7
#include <cstdio>
using namespace std;
int main(){
    char str[25] = "this is the char test";
    printf("%s",str);
    return 0;
}

输出结果：

1
this is the char test
布尔型

布尔型变量只能是true(真、非零)和false(假、零)。

强制类型转换

强制类型转换的格式如下：

(新类型名)变量名

符号常量和const常量

  • 符号常量通俗而言就是替换，也称为“宏定义”。
1
2
#define 标识符 常量
#define pi 3.14
  • 另一种定义常量的办法是const常量。
1
2
const 数据类型 变量名 = 常量;
const double pi = 3.14;

这两种写法都被称为常量，一旦确定其值后将无法改变。

运算符

算术运算符

关系运算符

逻辑运算符

条件运算符
1
A : B ? C
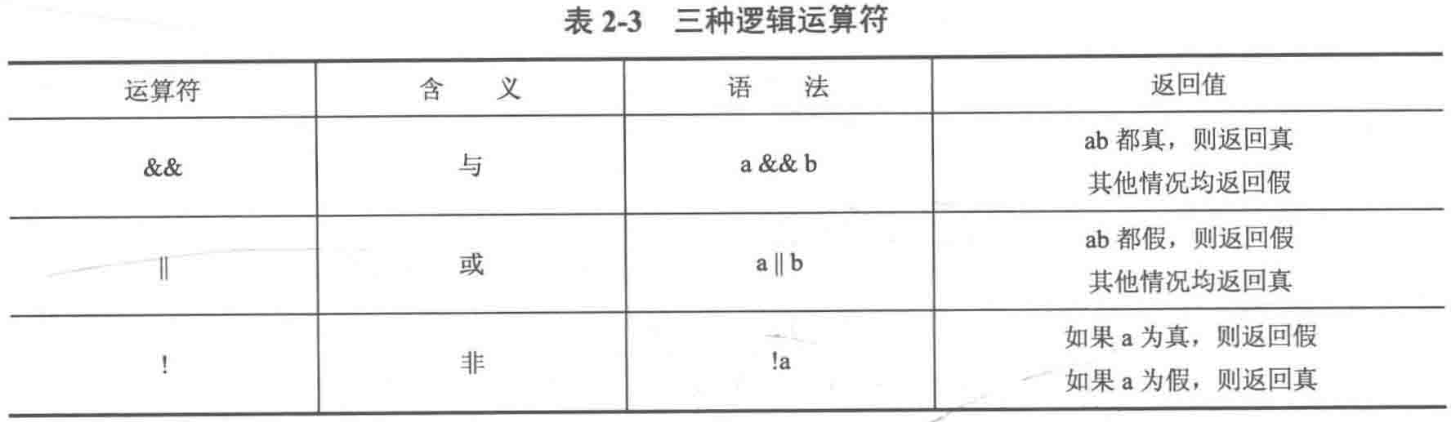
  • 如果A为真，执行并返回B的结果；如果A为假，那么执行并返回C的结果。
位运算符

顺序结构

使用scanf和printf输入/输出

scanf格式符

  • 注意上表中最后一行，数组名称本身就代表了这个数组第一个元素的地址，所以不需要加取地址运算符。因此在scanf中，除了char数组整个输入的情况不加&之外，其他变量类型都需要加&。

  • 注意字符数组使用%s读入的时候以空格和换行为读入结束的标志。

printf格式符

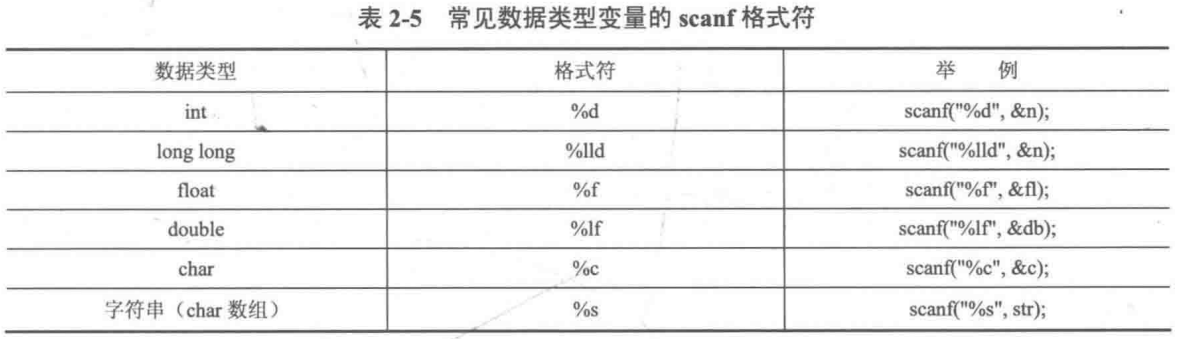
  • 对于double类型的变量，其在printf中的输出格式变成了%f，而在scanf中却是%lf。
三种实用的输出格式
%md
  • %md可以使不足m位的int型变量以m位进行右对齐输出，其中高位用空格补齐，如果变量本身超过m位，则保持原样。
1
2
3
4
5
6
7
8
9
#include <cstdio>
using namespace std;
int main(){
    int a = 123;
    int b = 12345678;
    printf("%5d\n",a);
    printf("%5d\n",b);
    return 0;
}
  • 输出：
1
2
  123
12345678
%0md
  • %0md只是在%md中间多加了0。和%md的唯一不同在于当变量不足m位时，将在前面补足够数量的0而不是空格。
1
2
3
4
5
6
7
8
9
#include <cstdio>
using namespace std;
int main(){
    int a = 123;
    int b = 12345678;
    printf("%05d\n",a);
    printf("%05d\n",b);
    return 0;
}
  • 输出：
1
2
00123
12345678
%.mf
  • %.mf可以让浮点数保留m位小数输出，精度是“四舍六入五成双”，具体而言为：
    • 5前为奇数，舍5入1；
    • 5前为偶数，舍5不进（0是偶数）。

使用getchar()和putchar()输入/输出字符

  • getchar()用来输入单个字符，putchar()用来输出单个字符。
  • getchar()可以识别并读入换行符。

typedef

  • typedef能够给复杂的数据类型起一个别名，这样在使用过程中就可以使用别名来替换原来的写法。
1
2
3
4
5
6
7
8
#include <cstdio>
using namespace std;
typedef long long LL;
int main(){
    LL a = 123456789123454321;
    printf("%lld\n",a);
    return 0;
}
  • 输出：
1
123456789123454321

选择结构

if语句

if语句的嵌套

switch语句

循环结构

while语句

  • 在while语句中，只要条件A成立就一直执行省略号里面的内容。

do…while语句

  • do…while语句会先执行省略号中的内容一次，然后才判断条件A是否成立，如果条件A成立，就继续反复执行省略号中的内容，直到某一次条件A不再成立，则退出循环。

for语句

  • for语句的具体格式如下：

break和continue语句

  • break语句不仅可以强制退出switch语句，而且break同样可以退出循环语句，即可以在需要的条件下直接退出循环。
  • continue语句的作用和break语句的作用有点相似，它可以在需要的地方临时结束循环的当前轮回，然后进入下一轮回。

数组

一维数组

  • 数组就是把相同数据类型的变量组合在一起而产生的数据集合，数组就是从某个地址开始连续若干个位置形成的元素集合。（数组的地址是连续存放的）
  • 一维数组的定义格式如下：
1
数据类型 数组名[数组大小]；
  • 数组大小必须是整数常量，不可以是变量。

冒泡排序

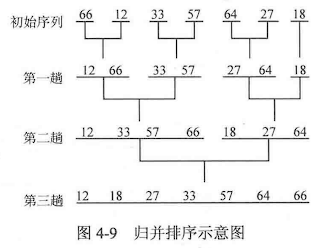
  • 冒泡的本质是在于交换，即每次通过交换的方式把当前剩余元素的最大值移动到一端，而当剩余元素减少为0时，排序结束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <cstdio>
#include <math.h>
using namespace std;
int main(){
    int temp = 0;
    int a[7] = {3,6,10,9,4,8,7};//n=7
    for(int i=1;i<=6;i++)//整个过程执行n-1趟
    {
        //每一趟中将左边元素与右边相邻元素依次对比，若大的数在左边，则交换这两个数
        //当该趟结束的时候，该趟的最大数被移到了该趟剩余数的最右边
        for(int j=0;j<7-i;j++)
        {
            if(a[j]>a[j+1])
            {
                temp = a[j];
                a[j] = a[j+1];
                a[j+1] = temp;
            }
        }
    }
    for(int i=0;i<=6;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}

二维数组

  • 二维数组是一位数组的扩展：
1
数据类型 数组名[第一维大小][第二维大小];
  • int a[5][6]数组的直观理解：

  • 特别提醒：如果数组的大小较大，大概在10610^6的级别，则需要定义在主函数外面，否则会使得程序异常退出，原因是函数内部申请的局部变量来自系统栈，所允许申请的空间较小；而函数外部申请的全局变量来自静态存储区，允许申请的空间较大。

memset——对数组中每个元素赋相同的初值

  • 需要注意的是：memset使用的是按字节赋值，即对每个字节赋相同的值，这样的话，在int型数组中每个数据的四个字节都会被分配为相同的值，因此为了避免出错，只建议对非char型的数组赋值为0和**-1**；

  • 使用memset对数组赋值时需要用#include<string.h>头文件；

  • memset函数的格式为：

1
memset(数组名，赋的数值，sizeof(数组名));

字符数组

字符数组的初始化
  • 和普通数组一样，字符数组也可以采用循环的方法初始化；
  • 除此之外，字符数组也可以通过直接赋值字符串来进行初始化（仅限于初始化，程序的其他位置不允许这样直接赋值整个字符串）
1
2
3
4
5
6
7
8
9
10
#include <cstdio>
using namespace std;
int main(){
    char str[10] = "YUGIN!";
    for(int i=0; i<6;i++)
    {
        printf("%c",str[i]);
    }
    return 0;
}
  • 输出：
1
YUGIN!
字符数组的输入输出
scanf输入，printf输出

  • scanf和printf对字符类型有%c和%s两种格式，其中%c用来输入单个字符，%s用来输入一个字符串并存在字符数组中。

  • %c格式能够识别空格和换行符并将其输入，%s通过空格或换行符来识别一个字符串的结束。

  • scanf在使用%s时，后面对应的数组名是不需要加&取地址运算符的。

1
2
3
4
5
6
7
8
#include <cstdio>
using namespace std;
int main(){
    char str[10];
    scanf("%s",str);
    printf("%s",str);
    return 0;
}
  • 输入输出：
1
2
输入：test test test
输出：test
getchar输入，putchar输出
  • getchar和putchar分别用来输入和输出单个字符；
  • 输入和输出示例：
1
2
3
4
5
6
7
8
9
10
#include <cstdio>
using namespace std;
int main(){
    char a;
    a=getchar();
    getchar();//可以用作吸收某些字符
    putchar(a);
    putchar('\n');
    return 0;
}
gets输入，puts输出
  • gets用来输入一行字符串（即一个一维数组，只有遇到\n时结束）
  • puts用来输出一行字符串（即一个一维数组，只有遇到\n时结束）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <cstdio>
using namespace std;
int main(){
    char a[20];
    char b[4][10];
    gets(a);
    for(int i=0;i<2;i++)
    {
        gets(b[i]);
    }
    puts(a);
    for(int i=0;i<2;i++)
    {
        puts(b[i]);
    }
    return 0;
}
  • 输入输出示例：
1
2
3
4
5
6
7
8
输入：
this is 
yugin's
blog
输出：
this is 
yugin's
blog
字符数组的存放方式
  • 由于字符数组是由若干个char类型的元素组成，因此字符数组的每一位都是一个char字符。
  • 在一维数组（或是二维数组的第二维）的末尾都有一个空字符\0，用于表示存放的字符串的结尾。

  • 特别注意：空字符\0的ASCII码为0，即空字符NULL，会占用一个字符位，因此在初始化的时候数组长度至少比字符串长度多一个长度。
  • 如果不是使用scanf函数的%s格式或gets函数输入字符串（例如使用getchar），则需要手动在字符数组最后加入\0，否则输出字符串会因为无法识别字符串末尾而输出乱码。

string.h头文件

  • string.h头文件包含了许多用于字符数组的函数。
strlen()函数
  • strlen()函数可以得到字符数组中第一个\0前的字符的个数并返回，其格式如下：
1
len = strlen(字符数组)；
strcmp()函数
  • strcmp函数返回两个字符串大小的比较结果，比较原则是字典序，其格式如下：
1
cmp = strcmp(字符数组1，字符数组2);
  • 字典序的解释：

strcpy()函数
  • strcpy()函数可以把一个字符串复制给另一个字符串，其格式如下：
1
2
strcpy(字符数组1,字符数组2);
puts(字符数组1);
  • 注意：是把字符数组2复制给字符数组1，包括结束符\0；
strcat()函数
  • strcat()可以把一个字符串接到另一个字符串后面，其格式如下：
1
2
strcpy(字符数组1,字符数组2);
puts(字符数组1);
  • 注意：是把字符数组2接到字符数组1后面；
sscanf()和sprintf()

  • sscanf()和sprintf()是处理字符串问题的利器！

  • sscanf()和sprintf()的使用格式如下：

1
2
sscanf(str,"%d",&n);
sprintf(str,"%d",n);
  • 上面sscanf()写法的作用是把字符数组str的中的内容以"%d"的格式写到n中（从左到右）。
1
2
3
4
5
6
7
8
9
10
#include <cstdio>
#include <string.h>
using namespace std;
int main(){
    char a[20] = "123";
    int n=0;
    sscanf(a,"%d",&n);
    printf("%d",n);
    return 0;
}
  • 输出：
1
123
  • 上面sprintf()写法的作用是把n以"%d"的格式写到str字符数组中（从右到左）。
1
2
3
4
5
6
7
8
9
10
#include <cstdio>
#include <string.h>
using namespace std;
int main(){
    char a[20];
    int n=123433;
    sprintf(a,"%d",n);
    printf("%s",a);
    return 0;
}
  • 输出：
1
123433
  • 上面的仅仅是简单的应用，实际上sscanf()和sprintf()可以进行更加复杂的字符串处理：
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <cstdio>
#include <string.h>
using namespace std;
int main(){
    char str[100];
    int n=520;
    double db=2002.080512121;
    char str2[20]="yugin!";
    char str3[20]="I";
    sprintf(str,"%s%d%s,%.4f",str3,n,str2,db);
    printf("%s",str);
    return 0;
}
  • 输出：
1
I520yugin!,2002.0805
  • 最后指出，sscanf()和sprintf()也可以支持正则表达式，则许多字符串问题将迎刃而解。

函数

  • 函数是一个实现一定功能的语句的集合，并在需要时可以反复调用而不必每次都重新写一遍。
  • 函数的基本语法格式：

全局变量

  • 全局变量是指在定义之后的所有程序段内都有效的变量（即定义在所有函数之前）

局部变量

  • 与全局变量相对，局部变量定义在函数内部，且只在函数内部生效，函数结束时局部变量便销毁。

再谈main()函数

  • 主函数对一个程序而言只有一个，且无论主函数写在哪个位置，整个程序一定是从主函数的第一个语句开始执行，然后在需要时再调用其他函数。
  • main()函数的结构：

以数组作为函数的参数

  • 函数的参数可以是数组，且数组作为参数时，参数中数组的第一维不需要填写长度（如果是二维数组，则第二维需要填写长度）
  • 数组作为参数时，在函数中对数组元素的修改就等同于对原素组进行修改（与普通的局部变量不同）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>
#include <string.h>
using namespace std;
//函数
void changStr(int a[],int b[][3])
{
    a[0]=1;
    a[1]=3;
    b[1][2]=5;
}
//主函数
int main(){
    int inter[5]={0};
    int in[2][3]={0};
    changStr(inter,in);
    printf("%d\n",inter[0]);
    printf("%d\n",inter[1]);
    printf("%d",in[1][2]);
    return 0;
}
  • 输出：
1
2
3
1
3
5
  • 注意：虽然数组可以作为参数，但是却不允许作为返回类型出现。

函数的嵌套调用

  • 函数的嵌套调用是指在一个函数中调用另一个函数，调用方式和main()函数调用其他函数一样。

函数递归调用

  • 函数递归调用是指一个函数调用该函数本身；

  • 类似下面计算n的阶乘的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <string.h>
using namespace std;
//函数
int F(int n)
{
    if(n==0) return 1;
    else return F(n-1)*n;
}
//主函数
int main(){
    int a=3;
    printf("%d",F(a));
    return 0;
}
  • 输出：
1
6

指针

什么是指针

  • 在C语言中，指针就是内存地址，指针变量是指用来存放内存地址的变量。
  • 在C/C++语言中，指针一般被认为是指针变量，指针变量的内容存储的是其指向的对象的首地址，指向的对象可以是变量（指针变量也是变量），数组，函数等占据存储空间的实体。
  • 只要在变量前面加上&，就表示变量的地址。
  • 指针是一个unsigned类型的函数。

指针变量

  • 指针变量是用来存放指针（或者可以理解为地址）。
  • 在某种数据类型后加*来表示这是一个指针变量，定义如下：
1
2
3
int *p;
double *p;
char *p;
  • 给指针变量赋值的方式一般是把变量的地址取出来，然后赋给对应类型的指针变量：
1
2
int a;
int *p = &a;
  • 如果p是指针（即p保存的是某个数据类型的地址），则*p就是这个地址所存放的元素：
1
2
3
4
5
6
7
8
9
10
11
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int main(){
    int a;
    int *p = &a;
    a=233;
    printf("%d",*p);
    return 0;
}
  • 输出：
1
233
  • 指针变量也可以进行加减法，其中减法的结果是两个地址偏移的距离。
  • 例如，对于int*类型的指针变量p而言，p+1是指p所指的int型变量的下一个int型变量地址，这个所谓的“下一个”是跨越了一整个int型（即4Byte）。
  • 指针变量也支持自增和自减的操作，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int main(){
    int a;
    int *p = &a;
    a=233;
    printf("%d\n",p);
    printf("%d\n",p+1);
    p++;
    printf("%d",p);
    return 0;
}
  • 输出：
1
2
3
113245364
113245368
113245368

指针与数组

  • 数组名称作为首地址使用，因此a == &a[0]和a+i == &a[i]成立。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int main(){
    int a[10]={1,2,4,5,7};
    int *p = a;
    int *q;
    printf("%d\n",p);
    q=&a[5];
    printf("%d\n",q);
    printf("%d",q-p);
    return 0;
}
  • 输出：
1
2
3
1241512688
1241512708
5
  • &a[0]和&a[5]之间相差5个int（4个Byte），因此输出5。

使用指针变量作为函数参数

  • 指针类型也可以作为函数参数的类型，这时视为把变量的地址传入函数。如果在函数中对这个地址中的元素进行改变，原先的数据就会确实地被改变。
  • 使用指针编写交换数据地函数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstdio>
#include <string.h>
using namespace std;
//交换函数
void my_swap(int *a,int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
//主函数
int main(){
    int a=1;
    int b=2;
    my_swap(&a,&b);
    printf("a=%d b=%d",a,b);
    return 0;
}
  • 输出：
1
a=2 b=1

引用

引用的含义
  • 引用是C++中一个强有力的语法，引用不产生副本，而是给原变量起了个别名。
  • 因此对引用变量操作就是对原变量操作。
  • 引用使用方法只需要在参数类型后面变量名前面加&就行，例子如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <string.h>
using namespace std;
//引用示例函数
void change(int &x)
{
    x=5;
}
//主函数
int main(){
    int b=88;
    change(b);
    printf("b=%d",b);
    return 0;
}
  • 输出：
1
b=5
  • 注意要把引用的&和取地址运算符&区分开来，引用并不是取地址的意思。
指针的引用
  • 通过引用和函数来更改变量指针的地址：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>
#include <string.h>
using namespace std;
//交换函数
void my_swap(int* &p1,int* &p2)
{
    int* temp = p1;
    p1 = p2;
    p2 = temp;
}
//主函数
int main(){
    int a=1;
    int b=2;
    int* p_a = &a;
    int* p_b = &b;
    my_swap(p_a,p_b);//必须用指针变量传入，引用不可以使用常量。
    printf("a=%d b=%d",*p_a,*p_b);
    return 0;
}
  • 输出：
1
a=2 b=1
  • 需要强调的是，引用是产生变量的别名，因此常量不可使用引用，上述代码不可写成my_swap(&a,&b);，必须用指针变量进行传入。

结构体(struct)的使用

结构体的定义

  • 定义一个结构体的基本格式如下：
1
2
3
struct Name{
  //一些基本的数据结构或者自定义的数据类型
};
  • 结构体可以这样定义：
1
2
3
4
5
6
struct studentInfo{
	int id;
	char gender;//'F'or'M'
	char name[20];
	char major[20];
}Alice,Bob,stu[1000];

  • 其中studentInfo是这个结构体的名字，内部定义了相关的数据。大括号外定义了结构体变量和结构体数组。

  • 结构体同样能够像基本数据类型那样定义：

1
2
studentInfo Alice;
studentInfo stu[1000];
  • 值得注意的是，结构体里面能够定义除了自己本身之外的任何数据类型。
1
2
3
4
struct node{
	node n;//不能定义node型变量，因为和本身一致
	node* next;//可以定义node*型指针变量
};
  • 虽然不能定义自己本身，但是可以定义自身类型的指针变量。

访问结构体内的元素

  • 访问结构体内的元素有两种方法："."和"->"操作。
  • 如果把studentInfo定义成如下：
1
2
3
4
5
struct studentInfo{
	int id;
	char gender;//'F'or'M'
	studentInfo* next;
}stu,*p;

  • 这样studentInfo中多了一个指针next用来指向下一个学生的地址，且结构体变量中定义了普通变量stu和指针变量p。

  • 因此访问stu中的变量的写法如下：

1
2
3
stu.id
stu.gender
stu.next
  • 访问指针变量p中的元素的写法如下：
1
2
3
(*p).id
(*p).gender
(*p).next
  • 还有一种访问结构体指针变量内元素更加简洁的写法：
1
2
3
p->id
p->gender
p->next

结构体的初始化

  • 结构体的初始化推荐使用构造函数的方法。
  • 构造函数的特点是函数名与结构体名一致而且不需要写返回函数。
  • 其中自己定义构造函数的格式如下：
1
2
3
4
5
6
7
8
9
10
struct studentInfo{
	int id;
	char gender;//'F'or'M'
	//以下构造函数的参数用于对结构体内部变量进行赋值
	studentInfo(int _id,char _gender)
	{
		id = _id;
		gender = _gender;
	}
};
  • 根据上述代码，即可直接对结构体的变量进行赋值：
1
studentInfo stu = studentInfo(20020805,'M');
  • 需要注意，如果自己重新定义了构造函数，则不能不经初始化就定义结构体变量，如下定义能够适应更多不同的场合：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct studentInfo{
	int id;
	char gender;//'F'or'M'
	//原始构造函数，用以不初始化就定义结构体变量
	studentInfo(){}
	//只初始化gender的构造函数
	studentInfo(char _gender)
	{
		gender = _gender;
	}
	//以下构造函数的参数用于对结构体内部两个变量进行赋值
	studentInfo(int _id,char _gender)
	{
		id = _id;
		gender = _gender;
	}
};

补充

cin和cout

  • cin和cout是C++的输入输出函数，需要添加头文件#include <iostream>和using namespace std;才能使用。
cin
  • cin采用输入运算符">>"来进行输入，例如
1
cin >> n >> db >> c >> str;
  • 如果想读入一整行，则需要getline函数：
1
2
char str[100];
cin.getline(str,100);
  • 如果是string容器，则需要使用以下方式输入：
1
2
char str[100];
getline(cin,str);
cout
  • cout采用输出运算符"<<"来进行输出，例如
1
cout << n << db << c << '\n' << str << endl;
  • endl和'\n'都是表示换行的意思。
  • 由于cin和cout在输入和输出大量数据时表现糟糕，因此不建议使用。

浮点数的比较

  • 由于计算机中采用有限二进制编码，存储并不总是准确，因此需要需要引入极小数eps来对这种误差进行纠正。
  • 圆周率pi的表达式可以使用acos(-1.0)来进行表示。
1
2
3
const double esp = 1e-8;
const double pi = acos(-1.0);
#define Equ(a,b) (fabs(a-b)<eps)

黑盒测试

单点测试

  • 对于单点测试而言，单点测试只需要按照正常逻辑执行一遍程序即可，是“一次性”的写法，即程序只需要一组数据能够完整执行即可。

多点测试

  • 对于多点测试，要求程序能够一次运行所有数据，并要求所有输出的结果都必须正确。
while…EOF型
  • 当题目没有说明有多少数据读入时，就可以利用scanf返回值是否为EOF来判断输入是否结束。
1
2
3
while(scanf("%d",&n) != EOF){
	...
}
  • 如果读入的是字符串，其对应写法如下：
1
2
3
4
5
6
while(scanf("%s",str) != EOF){
	...
}
while(gets(str) != NULL){
	...
}

入门模拟

再谈字符串输入输出

  • 在比较早的C/C++版本中，经常可以看到推荐使用gets函数来进行整行字符串的输入，就像下面这样的简单写法即可输入一整行：
1
gets(str);
  • 但是当输入的字符串长度超过数组长度上限MAX_LEN时，gets函数会把超出的部分也一并读进来，并且会覆盖数组之外的内存空间，这就导致了一定的安全风险，因此C++11标准将gets函数废弃了，然后在C++14时将该函数移除，如果现在想要整行输入的话，推荐使用cin.getline函数（见下文）。
1
cin.getline(str, MAX_LEN);
  • 例如下面一道例题：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//题目：输入一行字符串，然后直接输出这行字符串本身。
//输入描述：一行由大小写字母或空格组成的字符串，至少一个字符，不超过50个字符。
//输出描述：原样输出输入的字符串。
//**************************样例**************************
//输入：Huo Zhe Bu Jiu Shi Cang Cu Na Li You De Liao Ni Wo
//输出：Huo Zhe Bu Jiu Shi Cang Cu Na Li You De Liao Ni Wo
//**************************代码**************************
#include <cstdio>
#include <iostream>
using namespace std;
const int MAX_LEN = 1000000;
//主函数
int main(){
    char str[MAX_LEN];
    cin.getline(str,MAX_LEN);//由gets(str);函数换成了cin.getline(str,MAX_LEN);
    puts(str);
    return 0;
}

再谈sscanf()和sprintf()

关于sscanf()

  • sscanf是C语言标准库中的一个函数，用于从字符串中读取格式化输入。在C中也可以使用sscanf函数，但更常用的是使用C标准库中的stringstream类来进行字符串解析。

  • sscanf函数的原型如下：

1
int sscanf(const char* str, const char* format, ...);

  • 其中，str是要解析的字符串，format是格式化字符串，用于指定解析的规则，...是可变参数列表，用于接收解析出来的数据。

  • 与之相似的函数还有scanf和fscanf。其中，scanf从标准输入（通常是键盘）读取数据，而fscanf从文件中读取数据。

在使用sscanf函数时，需要注意以下几点：

  • format字符串中可以包含格式说明符，如 %d, %f, %s, %c, %x, %o, %u, %e, %g, %p, %n, 等等。
  • format字符串中可以包含空格、制表符、换行符等空白字符，用于跳过输入字符串中的空白字符。
  • format字符串中可以包含方括号 []，用于指定一个字符集合。例如，%[a-z] 表示匹配小写字母。
  • format字符串中可以包含星号 *，表示跳过该项输入。
  • sscanf() 函数返回成功匹配并赋值的个数。如果返回值小于参数个数，则表示解析失败。

基于最后一条性质可以实现下述例题：

  • 题目描述：
1
2
3
4
5
6
7
给定一个字符串，它可能是以下三种格式中的一种：
A is greater than B
A is equal to B plus C
No Information
其中前两种情况中的A、B、C均为正整数，而第三种情况中没有数字。请确认字符串代表的信息是否从算术上成立，如果成立，那么输出Yes；否则输出No；如果是第三种情况，那么输出三个问号（即???）。
注：
1、请将字符串整行读入后使用sscanf函数进行处理
  • 输入描述：
1
一行满足题意的字符串，其中A、B、C为不超过100的正整数。
  • 输出描述：
1
根据题意输出Yes、No或???。
  • 样例：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
*******************样例1*****************
输入:
10 is greater than 5
输出:
Yes
*******************样例2*****************
输入:
6 is equal to 1 plus 3
输出:
No
*******************样例3*****************
输入:
No Information
输出:
???
  • 实现代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <cstdio>
#include <iostream>
#include <string.h>
using namespace std;
const int MAX_LEN = 1000;
//主函数
int main(){
    int A = 0,B = 0,C = 0;
    char str[MAX_LEN];
    cin.getline(str,MAX_LEN);
    if(sscanf(str,"%d is greater than %d",&A,&B) == 2)//利用sscanf() 函数返回成功匹配并赋值的个数。
    {
       if(A>B)
       {
           printf("Yes");
       }
       else
       {
           printf("No");
       }
    }
    else if(sscanf(str,"%d is equal to %d plus %d",&A,&B,&C) == 3)//利用sscanf() 函数返回成功匹配并赋值的个数。
    {
        if(A==B+C)
        {
            printf("Yes");
        }
        else
        {
            printf("No");
        }
    }
    else
    {
        printf("???");
    }
    return 0;
}
  • 总结：利用sscanf() 函数返回成功匹配并赋值的个数，从而能够很好地解决问题。

关于sprintf()

  • sprintf是C语言标准库中的一个函数，用于将格式化的数据写入字符串中。在C中也可以使用sprintf函数，但更常用的是使用C标准库中的ostringstream类来进行字符串解析。

  • sprintf函数的原型如下：

1
int sprintf(char *str, const char *format, ...);

  • 其中，str是要写入的字符串，format是格式化字符串，用于指定写入的规则，...是可变参数列表，用于接收要写入的数据。

  • 与之相似的函数还有printf和fprintf。其中，printf将输出写入标准输出（通常是屏幕），而fprintf将输出写入文件。

在使用sprintf函数时，需要注意以下几点：

  • format字符串中可以包含格式说明符，如 %d, %f, %s, %c, %x, %o, %u, %e, %g, %p, %n, 等等。
  • format字符串中可以包含空格、制表符、换行符等空白字符，用于控制输出格式。
  • format字符串中可以包含方括号 []，用于指定一个字符集合。例如，%[a-z] 表示匹配小写字母。
  • sprintf() **函数返回成功写入的字符数。**如果返回值小于0，则表示写入失败。

例题：sprintf函数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <cstdio>
#include <iostream>
#include <string.h>
using namespace std;
const int MAX_LEN = 1000;
//主函数
int main(){
    char str[MAX_LEN];
    int year,month,day,hour,minute,second;
    scanf("%d %d %d %d %d %d",&year,&month,&day,&hour,&minute,&second);
    sprintf(str,"%04d-%02d-%02d %02d:%02d:%02d",year,month,day,hour,minute,second);//注意此处的ssprintf()函数注释将需要的字符串写入到字符串数组中
    printf("%s",str);//注意此处字符串数组需要采用printf()函数进行输出
    return 0;
}

  • 总结：

  • 注意代码中的ssprintf()函数注释将需要的字符串写入到字符串数组中；

  • 注意代码最后的输出字符串数组需要采用printf()函数进行输出。

再谈结构体与函数数组传参

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <cstdio>
#include <string.h>
//结构体
struct Student {
    int id;
    char name[15];
    //构造函数
    Student(){}
    Student(int _id,char _name[]){//函数中的数组传参
        id = _id;
        strcpy(name,_name);//复制字符串数组
    }
};
//主函数
int main() {
    Student student;
    char name[15];
    int id;
    scanf("%d",&id);
    getchar();
    scanf("%s",name);//读入字符串。
    student = Student(id,name);
    printf("%d\n%s",student.id,student.name);
    return 0;
}
  • 总结：注意上述代码中的函数数组传参，以及字符串数组赋值；
  • 注意如何利用scanf()函数读入字符串。

再谈cin和cout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <cstdio>
#include <string.h>
#include <iostream>
#include <iomanip>//数据格式控制函数的头文件
const int MAX_LEN  = 200;
using namespace std;
//主函数
int main(){
    int a;
    double b;
    char str[MAX_LEN];
    cin >> a >> b;
    getchar();
    cin.getline(str,MAX_LEN);
    //fixed()函数与setprecision(int n)并用，可以控制小数点后面有n位。注意：setprecision()函数是控制有效数字的位数，而fixed()函数与setprecision(int n )函数结合使用是保留小数点后的位数，小数点的保留采用四舍五入！
    cout << a << endl << fixed << setprecision(2) << b << endl << str;
    return 0;
}
  • 总结：
  • #include <iomanip>是数据格式控制函数的头文件；
  • 在使用cout函数输出的时候fixed()函数与setprecision(int n)并用，可以控制小数点后面有n位。注意：setprecision()函数是控制有效数字的位数，而fixed()函数与setprecision(int n )函数结合使用是保留小数点后的位数，小数点的保留采用四舍五入！
  • 如果只使用setprecision(int n) 函数效果如下：
1
2
3
4
5
cout << setprecision(3) << 0.12345 << endl;
cout << setprecision(3) << 1.23456 << endl;
输出：
0.123
1.23
  • 当要保留对应位数的小数(四舍五入)的时候，就需要采用fixed()函数，效果如下：
1
2
3
4
5
cout << fixed << setprecision(3) << 0.12345 << endl;
cout << fixed << setprecision(3) << 1.23456 << endl;
输出：
0.123
1.235

再谈浮点精度比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <cstdio>
#include <string.h>
#include <cmath>
using namespace std;
const double eps = 1e-8;
//主函数
int main(){
    int a,b,c,d;
    scanf("%d%d%d%d",&a,&b,&c,&d);
    double res1 = a* asin(sqrt(b) / 2);
    double res2 = c* asin(sqrt(d) / 2);
    if(res1 - res2 > eps)//公式1>公式2
    {
        printf("1");
    }
    else if(res2 - res1 > eps)//公式2>公式1
    {
        printf("2");
    }
    else
    {
        printf("0");
    }
    return 0;
}
  • 总结：一般为了避免计算机精度误差造成浮点数大小比较不准，采用浮点数常量大小为const double eps = 1e-8;的数据来进行区分。

再谈if语句

  • if(a==b==0)和if(a==0&&b==0)的区别：
  • 这两个表达式的区别在于它们的运算顺序不同。
    • if(a==b==0)的运算顺序是先比较a和b是否相等(a==b)，然后再将结果与0比较。如果a和b都为0，但是true不等于0，所以表达式a==b==0为false。而当a和b不相等时，表达式a==b==0为true。
    • if(a==0&&b==0)的运算顺序是先判断a是否等于0，然后再判断b是否等于0。只有当a和b都等于0时，这个表达式的结果才为true；否则，结果为false。
    • 因此，这两个表达式的含义是不同的。需要特别注意！

再谈数字转换字符串

  • to_string() 是 C++11 中的标准库函数，它将数字转换为字符串，并可以接受任何数字类型，需要包含 #include <sstream> 头文件。

简单模拟

  • 简单模拟的题目不涉及算法，一般完全根据题目描述来进行代码编写，考察的是代码能力！

例题：2的幂

  • 代码：
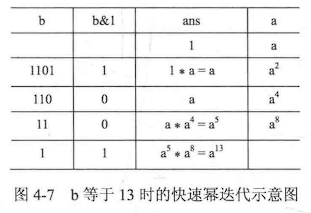
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <cstdio>
#include <string.h>
#include <cmath>
using namespace std;
const int m = 1007;
//主函数
int main(){
    int num;
    scanf("%d",&num);
    int res=1;
    for(int i=1;i<=num;i++)
    {
        res = ((res%m)*(2%m))%m;
    }
    printf("%d",res);
    return 0;
}
  • 总结：该题的数据大小远大于C++中的long long类型，因此不能直接进行计算，需要根据题目提示的公式进行简化，从而正确计算得到结果！

例题：B1032 挖掘机技术哪家强

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int list_chengji[100010]={0};
int main(){
    int num;
    int max_chengji=-1;//注意此处最大成绩设置为-1，否则无法通过最大成绩就是为0的测试点。
    int xuhao,chengji,res_xuhao;
    scanf("%d",&num);
    for(int i=0;i<num;i++){
        scanf("%d %d",&xuhao,&chengji);
        list_chengji[xuhao]+=chengji;
    }
    for(int k=1;k<100010;k++)
    {
        if(list_chengji[k]>max_chengji)
        {
            max_chengji = list_chengji[k];
            res_xuhao = k;
        }
    }
    printf("%d %d\n",res_xuhao,max_chengji);
    return 0;
}
  • 总结：这道题目要细心，注意在代码中计算最大成绩的时候初始值要设置为-1，否则无法通过最大成绩就是为0的测试点。

查找元素

  • 查找元素类题目：给定一些元素，然后查找某个满足某条件的元素。
  • 一般而言，如果需要在一个比较小范围的数据集中查找，那么直接遍历每一个数据即可。
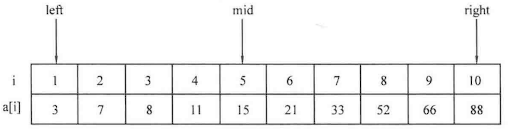
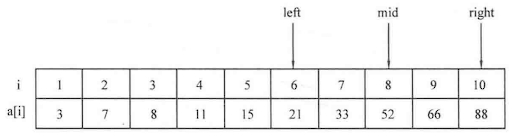
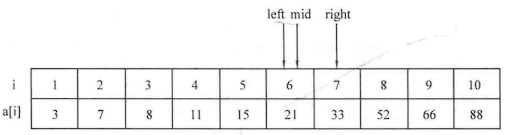
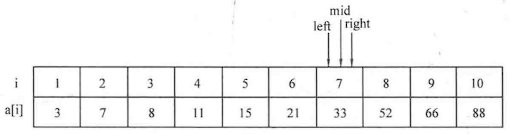
  • 如果需要查找的范围比较大，可以采用二分查找等算法来进行更快速的查找。

例题：寻找元素对

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int main(){
    int n;
    scanf("%d",&n);
    int list[1010];
    for(int i=0;i<n;i++)
    {
        scanf("%d",&list[i]);
    }
    int x,flag=0;
    scanf("%d",&x);
    for(int k=0;k<n-1;k++)
    {
        for(int j=k+1;j<n;j++)
        {
            if(x==list[k]+list[j])
            {
                flag++;
            }
        }
    }
    printf("%d",flag);
    return 0;
}

图形输出

  • 所谓图形，其实是由若干字符组成，因此只需要弄清楚规则就能编写代码，有以下两种方法：
    • 通过规律直接进行输出；
    • 定义一个二维字符数组，通过规律填充字符数组，最后再输出整个二维数组。

例题：画X

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <cstdio>
#include <string.h>
using namespace std;
//主函数
int main(){
    int n;
    char list[101][101];
    memset(list,' ',sizeof(list));//初始化数组
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        for(int k=0;k<n;k++)
        {
            if(i<n/2||i>n/2)
            {
                if(k==i||k==n-1-i)
                {
                    list[i][k]='*';
                }
            }
            else if(i==n/2)
            {
                if(k==i)
                {
                    list[i][k]='*';
                }
            }
        }
    }
    for(int i=0;i<n;i++)
    {
        if(i<=n/2)
        {
            for(int k=0;k<n-i;k++)
            {
                printf("%c",list[i][k]);
            }
        }
        else
        {
            for(int k=0;k<=i;k++)
            {
                printf("%c",list[i][k]);
            }
        }
        printf("\n");
    }
    return 0;
}
  • 总结：这类型题目主要在于找到图案的规律，若图案比较复杂可以放在二维字符数组中进行输出，注意一下二维字符数组的初始化可以采用memset(list,' ',sizeof(list));函数！

日期处理

  • 日期处理问题主要考虑平年和闰年的关系(由此产生的二月天数之间的差别)、大月和小月的问题，细节比较繁杂！

例题：周几

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <cstdio>
#include <string.h>
using namespace std;
//初始化平年闰年的数组
//0是平年，1是闰年
int year_list[2][13]={
        {0,31,28,31,30,31,30,31,31,30,31,30,31},
        {0,31,29,31,30,31,30,31,31,30,31,30,31}
};
//是否闰年判断函数
bool leap_year(int year)
{
    if(year%400==0||(year%4==0&&year%100!=0))
    {
        return true;
    }
    else
    {
        return false;
    }
}
//判断日期前后,如果day在day1之前就是true，否则为false
bool before_afer(int year,int month,int day,int year1,int month1,int day1)
{
    if(year1-year>0)
    {
        return true;
    }
    else if(year1-year<0)
    {
        return false;
    }
    else if(year1-year==0)
    {
        if(month1-month>0)
        {
            return true;
        }
        else if(month1-month<0)
        {
            return false;
        }
        else if(month1==month)
        {
            if(day1-day>0)
            {
                return true;
            }
            else if(day1-day<=0)
            {
                return false;
            }
        }
    }
}
//计算两个日期之间的天数差值,day在day1之前，采用日期减法
int count_days(int year,int month,int day,int year1,int month1,int day1)
{
    int num=0;
    if(year1==year&&month1==month&&day1==day)
    {
        return 0;
    }
    else
    {
        while(true)
        {
            day1--;
            if(day1<1)
            {
                month1--;
                if(month1<1)
                {
                    year1--;
                    month1=12;
                }
                day1=year_list[leap_year(year1)][month1];
            }
            num++;
            if(year1==year&&month1==month&&day1==day)
            {
                break;
            }
        }
        return num;
    }
}
//主函数
int main(){
    int year,month,day;
    scanf("%d-%d-%d",&year,&month,&day);
    int num=0,shengyu=0;
    //2021-05-02是周日，用0表示（用这个日期作为基准）
    bool b_a = before_afer(2021,5,2,year,month,day);
    if(b_a)
    {
        num=count_days(2021,5,2,year,month,day);
        shengyu=num%7;
        printf("%d",shengyu);
    }
    else
    {
        num=count_days(year,month,day,2021,5,2);
        shengyu=num%7;
        if(shengyu==0)
        {
            printf("%d",0);
        }
        else
        {
            printf("%d",7-shengyu);
        }
    }
    return 0;
}

  • 总结：虽然本题我采用了日期减法作为函数进行运算，但是和日期加法的想法相似，主要思想如下：

    • 直接给日期加上指定的天数并不是很容易的事情，所以我们可以换个思路，每次只加1天，一直加到指定的天数为止。这样我们就把问题转换为计算加1天之后的新日期，而这个问题就相对简单许多。
    • 假设当前日期的年、月、日分别是year、month、day，那么加一天之后 day 就变成了 day+1，之后我们需要判断这个新的day是否超过了当前月份month 所拥有的总天数，如果没超过，那么相安无事，算法结束；如果超过了，那么就需要令月份month 加 1、同时让day重置为 1（即把日期变为下一个月的 1 号）。接下来，如果加了 1 之后的月份 month 变为了 13 月，那么就需要令年份year加 1、同时置月份 month重置为 1（即把日期变为下一年的 1 月）。
    • 这个过程需要知道每个月有多少天，为了方便直接取出每个月的天数，不妨设置一个二维数组int year_list[2][13]，用来存放每个月的天数，其中第一维为 0 时表示平年，为 1 时表示闰年。至于平年和闰年的判断方式也很简单：年份是 400 的倍数时是闰年，年份是 4 的倍数但不是 100 的倍数时也是闰年，其他情况都是平年。
    • 代码如下：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    #include <cstdio>
    #include <string.h>
    using namespace std;
    //初始化平年闰年的数组
    //0是平年，1是闰年
    int year_list[2][13]={
            {0,31,28,31,30,31,30,31,31,30,31,30,31},
            {0,31,29,31,30,31,30,31,31,30,31,30,31}
    };
    //是否闰年判断函数
    bool leap_year(int year)
    {
        if(year%400==0||(year%4==0&&year%100!=0))
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    //主函数
    int main(){
        int year,month,day;
        scanf("%d-%d-%d",&year,&month,&day);
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            day++;
            if(day>year_list[leap_year(year)][month])
            {
                month++;
                day=1;
                if(month>12)
                {
                    year++;
                    month=1;
                }
            }
        }
        printf("%04d-%02d-%02d", year, month, day);   // 按格式输出年月日
        return 0;
    }
    • 最后，这道例题的思考方式如下：首先确认一个基准日期->(2021-05-02是周日，用0表示)->计算输入的日期在基准日期之前或者之后->计算相差多少天->最后计算输入的日期是周几！
    • 通过上述步骤，该题迎刃而解！

进制转换

对于一个p进制数需要转换为q进制数，一般需要分为以下两步：

  • p进制数x转十进制数y：

    • 实现代码：
1
2
3
4
5
6
7
8
9
10
11
12
//p进制数x转10进制数y的函数
int p_ten(int x,int p)
{
    int y=0,product=1;
    while(x!=0)
    {
        y=y+(x%10)*product;
        x=x/10;
        product=product*p;
    }
    return y;
}

  • 十进制数y转q进制数z的函数(除基取余法)：

    • 采用"除基取余法"，意思是每次将带转换的数除q，将得到的余数作为低位存储，而商继续除q并进行上面的操作，最后当商为0时，将所有位从高到低输出就可以得到z！

    • 例如十进制数11转换为二进制：

    • 实现代码：

    • 代码中采用do...while而不是while的原因是如果十进制恰好是0会造成直接跳出循环导致结果出错，因此采用do...while语句。

1
2
3
4
5
6
7
8
9
10
11
//十进制数y转q进制数z的函数(除基取余法)
int ten_q(int y,int q,int z_list[])
{
    int num=0,z=0;
    do {
        z_list[num]=y%q;
        num++;
        y=y/q;
    }while(y!=0);
    return num;
}

例题：K进制转十进制

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <cstdio>
#include <string.h>
#include <cmath>
using namespace std;
//p进制数x转10进制数y的函数
int p_ten(int x,int p)
{
    int y=0,product=1;
    while(x!=0)
    {
        y=y+(x%10)*product;
        x=x/10;
        product=product*p;
    }
    return y;
}
//十进制数y转q进制数z的函数(除基取余法)
int ten_q(int y,int q,int z_list[])
{
    int num=0,z=0;
    do {
        z_list[num]=y%q;
        num++;
        y=y/q;
    }while(y!=0);
    return num;
}
//主函数
int main(){
    char str[10];//用于存储k进制串
    int k,str_len;
    int sum=0;
    scanf("%s %d",str,&k);
    str_len = strlen(str);
    for(int i=0;i<str_len;i++)
    {
        if(str[i]>='A'&&str[i]<='F')
        {
            sum+=(str[i]-'A'+10)*pow(k,str_len-1-i);
        }
        else
        {
            sum+=(str[i]-'0')*pow(k,str_len-1-i);
        }
    }
    printf("%d",sum);
    return 0;
}
  • 总结：这道例题无法直接使用上述两个函数，因此需要根据题意重新构造，但是难度不大，需要处理十进制以上的数据。

字符串处理

  • 字符串处理类题目可能实现逻辑比较麻烦，而且需要考虑许多细节和边界情况，因此是一种很好体现代码能力的题型。

例题：单词倒序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#include <string.h>
#include <iostream>
using namespace std;
const int MAXN = 1010;
//主函数   
int main(){
    char str[MAXN],str2[MAXN];
    cin.getline(str,MAXN);
    int str_len = strlen(str);
    int flag=0,m=0;
    for(int i=str_len-1;i>=0;i--)
    {
        flag++;
        if(str[i]==' ')
        {
            for(int j=i+1;j<=i+flag-1;j++)
            {
                str2[m]=str[j];
                m++;
            }
            str2[m]=' ';
            m++;
            flag=0;
        }
        else if(i==0)
        {
            for(int j=i;j<=i+flag-1;j++)
            {
                str2[m]=str[j];
                m++;
            }
            str2[m]=' ';
            m++;
            flag=0;
        }
    }
    str2[str_len]='\0';
    for(int k=0;k<str_len;k++)
    {
        printf("%c",str2[k]);
    }
    return 0;
}
  • 总结：细心分析，按照逻辑编写代码，问题即可迎刃而解。

例题：公共前缀

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 55;
//主函数
int main(){
    char str[MAXN][MAXN];
    int n;
    int min_strlen=100,num=0,flag=0;
    scanf("%d",&n);
    getchar();//吸收换行符
    for(int i=0;i<n;i++)
    {
        cin.getline(str[i],MAXN);
        if(min_strlen>(int)strlen(str[i]))
        {
            min_strlen=(int)strlen(str[i]);
        }
    }
    for(int i=0;i<min_strlen;i++)
    {
        for(int k=0;k<n-1;k++)
        {
            if(str[k][i]!=str[k+1][i])
            {
                flag++;
            }
        }
        if(flag)
        {
            num=i-1;
            break;
        }
        num=i;
    }
    //printf("%d",min_strlen);
    for(int i=0;i<=num;i++)
    {
        printf("%c",str[0][i]);
    }
    return 0;
}
  • 总结：注意一下本题中在需要使用循环输入的时候要采用getchar();函数吸收一下换行符，否则换行符会输入至字符数组中！

C++标准模板库(STL)介绍

vector的常见用法详解

  • vector->变长数组，即"长度根据需要而自动改变的数组";
  • 要使用 vector，需要添加 vector 头文件，即 #include <vector>;

vector 的定义

  • 单独定义一个 vector：
1
vector<typename> name;
  • 上面 vector<typename> name 的定义相当于一维数组 typename name[size] ，只是其长度可以根据需要进行变化，比较节省空间->变长数组。
  • 与一维数组一样，上述 typename 可以是任何基本类型，如 int、double、char、结构体等；
  • 也可以是 STL 标准容器，如 vector、set、queue 等；
  • 如果 typename 也是一个 STL 容器，定义的时候需要将 >> 变为 > >:
1
vector<vector<int> > name;//>>要加上空格
  • 对于二维数组定义，有以下两种方法：
  1. 第一种定义方法：
1
2
vector<typename> Arrayname[arraySize];
vector<int> vi[100];
  • 这样 Arrayname[0] 至 Arrayname[arraySize-1] 中每一个都是一个 vector 容器。
  1. 第二种定义方法：
1
vector<vector<int> > Arrayname;//>>要加上空格
  • 与第一种定义方法不同，上述写法的一维长度已经固定为 arraySize，另一维才是“变长”的；
  • 而第二种写法两个维度都是“变长”的。

vector 容器内元素的访问

vector 一般有一下两种访问方式：

  1. 通过下标访问
  2. 通过迭代器访问
通过下标访问
  • 与访问普通数组一样，对于一个定义为 vector<int> vi; 的 vector 的容器而言，直接访问 vi[index] 即可（如 vi[0]、vi[1]）。
  • 当然，下标是从 0 到 vi.size ()-1,否则访问超出这个范围内的元素可能会运行出错。
通过迭代器访问
  • 迭代器 (iterator)可以理解为一种类似指针的东西，其定义如下：
1
vector<typename>::iterator it;
  • 这样 it 就是一个 vector<typename>::iterator 型的变量，其中 typename 就是定义 vector 时填写的类型。
  • 得到迭代器 it，就可以通过 *it 来访问 vector 里的元素。
1
2
3
4
5
vector<int> vi;
for(int i=1;i<=5;i++)
{
	vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
}
  • 可以通过类似下标和指针访问数组的方式来访问容器内的元素：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    //vi.begin()为取vi的首元素地址，而it指向这个地址
    vector<int>::iterator it = vi.begin();
    for(int i=0;i<5;i++)
    {
        printf("%d ",*(it+i));//输出vi[i]
    }
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出结果：
1
1 2 3 4 5
  • 从上述程序不难看出，vi[i]和*(vi.begin()+i)是等价的。
  • 关于 vector 两个函数的说明：
  1. vi.begin() 函数的作用是为取 vi 的首元素地址；
  2. vi.end() 函数的作用是取尾元素地址的下一个地址，end() 作为迭代器的末尾标志，不存储任何元素。
  • 除此之外，迭代器还实现了两种自加（自减操作同理）操作：
  1. ++it 和 --it
  2. it++和 it--
  • 于是有另一种遍历 vector 中元素的写法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
	    vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    //vector的迭代器不支持it<vi.end()写法，因此循环条件只能使用it!=vi.end()
    vector<int>::iterator it = vi.begin();
    for(it=vi.begin();it!=vi.end();it++)
    {
        printf("%d ",*it);
    }
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1 2 3 4 5
  • 需要指出的是，在常用 STL 容器中，只有在 vector 和 string 中，才允许使用类似于 vi.begin()+3 这种迭代器加上整数的写法。

vector 常用函数实例解析

push_back()
  • 顾名思义，push_back(x) 就是在 vector 后面添加一个元素 x，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
vector<int> vi;
for(int i=1;i<=5;i++)
{
	vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
pop_back()
  • 有添加就有删除，pop_back() 用以删除 vector 的尾元素，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    vi.pop_back();//删除vi的尾元素5
    //vi.begin()为取vi的首元素地址，而it指向这个地址
    vector<int>::iterator it = vi.begin();
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i]
    }
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1 2 3 4
size()
  • size() 用来获取 vector 中的元素个数，时间复杂度为 O(1)O(1)。size() 返回的是 unsigned 类型，不过一般而言使用 %d 不会出现太大问题。这一点，对于所有 STL 容器都是一样的。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    printf("%d",vi.size());
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
5
clear()
  • clear() 用来清空 vector 中的所有元素，时间复杂度为 O(N)O(N)，其中 N 为 vector 中元素的个数。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    vi.clear();
    printf("%d",vi.size());
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
0
insert()
  • insert(it,x) 用来向 vector 的任意迭代器 it 处插入一个元素 x，时间复杂度 O(N)O(N)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    vector<int>::iterator it = vi.begin();
    vi.insert(it+2,-1);
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i],1 2 -1 3 4 5 
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1 2 -1 3 4 5
erase()
  • erase() 有两种用法：删除单个元素和删除一个区间内的所有元素。时间复杂度为 O(N)O(N)。
  1. 删除单个元素
  • erase(it) 即删除迭代器为 it 处的元素。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    vector<int>::iterator it = vi.begin();
    vi.insert(it+2,-1);
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i],1 2 -1 3 4 5 
    }
    printf("\n");
    vi.erase(it+2);
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i],1 2 3 4 5 
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
1 2 -1 3 4 5 
1 2 3 4 5
  1. 删除一个区间内的所有元素
  • erase(first, last) 即删除 [first, last) 内的所有元素。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
    vector<int> vi;
    for(int i=1;i<=5;i++)
    {
        vi.push_back(i);//vi.push_back(i);是在vi的末尾添加元素i，即添加1 2 3 4 5
    }
    vector<int>::iterator it = vi.begin();
    vi.insert(it+2,-1);
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i],1 2 -1 3 4 5 
    }
    printf("\n");
    vi.erase(it+2,it+4);
    for(int i=0;i<vi.size();i++)
    {
        printf("%d ",*(it+i));//输出vi[i],1 2 4 5 
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
1 2 -1 3 4 5 
1 2 4 5
  • 由上面的内容可以知道，要删除 vector 内的所有元素，可以使用 vi.erase(vi.begin(),vi.end());
  • 当然，最方便的方法是使用 vi.clear()。

vector 的常见用途

存储数据
  1. vector 本身可以作为数组使用，而且在一些元素个数不确定的场合可以很好地节省空间。
  2. 有些场合需要根据一些条件把部分数据输出在同一行，数据中间用空格隔开。由于输出数据的个数是不确定的，为了更方便地处理最后一个满足条件的数据后面不输出额外的空格，可以先用 vector 记录所有需要输出的数据，最后一次性输出。
用邻接表存储图
  1. 使用 vector 实现邻接表可以让一些对指针不太熟悉的使用者有一个比较方便的写法。

vector 的例题

例题：子集I

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
vector<vector<int> > result;
vector<int> temp;
int n;
//递归输出子集1函数
void F(int index)
{
    //递归边界
    if(index == n+1)
    {
        result.push_back(temp);
    }
    //递归式
    else
    {
        temp.push_back(index);
        F(index+1);
        temp.pop_back();
        F(index+1);
    }
}
//比较函数，从小到大排序
bool cmp(vector<int> &a,vector<int> &b)//引用的写法
{
    if(a.size()!=b.size())
        return a.size()<b.size();
    else
        return a<b;
}
//主函数
int main(){
    scanf("%d",&n);
    F(1);
    sort(result.begin(),result.end(),cmp);
    for(int i=0;i<result.size();i++)
    {
        for(int j=0;j<result[i].size();j++)
        {
            printf("%d",result[i][j]);
            if(j!=result[i].size()-1)
                printf(" ");
        }
        printf("\n");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目巧妙应用了 vector 是变长数组的特性，并且使用递归的方法实现。注意对二维 vector 变量进行排序的时候可以使用引用的方法。

例题：子集III

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
vector<vector<int> > result;
vector<int> temp;
int num[15];
int n;
//递归输出子集1函数
void F(int index)
{
    //递归边界
    if(index == n+1)
    {
        result.push_back(temp);
    }
        //递归式
    else
    {
        temp.push_back(num[index]);
        F(index+1);
        temp.pop_back();
        F(index+1);
    }
}
//比较函数，从小到大排序
bool cmp(vector<int> &a,vector<int> &b)//引用的写法
{
    if(a.size()!=b.size())
        return a.size()<b.size();
    else
        return a<b;
}
//主函数
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&num[i]);
    }
    F(1);
    sort(result.begin(),result.end(),cmp);
    vector<vector<int> >::iterator it = result.begin();
    for(int i=0;i<result.size()-1;i++)
    {
        if(result[i].size()==result[i+1].size())
        {
            int flag=0;
            for(int j=0;j<result[i].size();j++)
            {
                if(result[i][j]!=result[i+1][j])
                {
                    flag++;
                }
            }
            if(!flag)
            {
                result.erase(it+i+1);
                i--;
            }
        }
    }
	//剔除重复部分
    for(int i=0;i<result.size();i++)
    {
        for(int j=0;j<result[i].size();j++)
        {
            printf("%d",result[i][j]);
            if(j!=result[i].size()-1)
                printf(" ");
        }
        printf("\n");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目相较于第一题多了剔除重复部分的代码。

例题：单词排列

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
using namespace std;
const int MAX = 300;
int n;
bool hashTable[MAX] = {false};
string str,temp;
vector<string> result;
//递归输出单词排序数
void F(int index)
{
    //递归边界
    if(index == n)
    {
        result.push_back(temp);
    }
    //递归式
    for(int k=0;k<n;k++)
    {
        if(!hashTable[str[k]])
        {
            hashTable[str[k]]=true;
            temp.push_back(str[k]);
            F(index+1);
            hashTable[str[k]]=false;
            temp.pop_back();
        }
    }
}
//主函数
int main(){
    cin>>str;
    n=str.length();
    F(0);
    sort(result.begin(),result.end());//按照字典序排列
    for(int i = 0; i < result.size(); i++) {
        cout << result[i] << endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题思路与全排列的题目是一致，需要注意的是 string 和 vector 的用法

set 的常见用法详解

  • set 翻译为集合，是一个内部自动有序而且不包含重复元素的容器；
  • 当有可能出现需要去掉重复元素的情况，而且有可能因为这些元素比较大或者类型不是 int 型而不能直接开散列表；
  • 上述情况可以使用 set 来保留元素本身而不考虑它的个数，而且 set 提供了更为直观的接口，并且加入 set 之后可以实现自动排序；
  • 要使用 set，需要添加 set 头文件，即 #include <set>,并且需要加上using namespace std;

set 的定义

  • 单独定义一个 set：
1
set<typename> name;
  • typename 依然可以是任何基本类型，如 int、double、char、结构体等，或者是 STL 标准容器，例如 vector、set、queue 等。
1
2
set<int> num;
set<vector<int> > num;
  • set 数组定义和 vector 也相同：
1
2
set<typename> Arrayname[arraySize];
set<int> a[100];
  • 这样 Arrayname[0] 到 Arrayname[arraySize-1] 中每一个都是一个 set 容器。

set 容器内元素的访问

  • set 只能通过迭代器 (iterator)访问：
1
2
3
set<typename>::iterator it;
set<int>::iterator it;
set<char>::iterator it;
  • 这样就得到了迭代器 it，并且可以通过 *it 来访问 set 里的元素。
  • 值得注意的是，除了 vector 和 string 之外的 STL 容器都不支持 *(it+i) 的访问方式，因此只能按照以下方式枚举：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    //注意，不支持it < st.end()的写法
    for(set<int>::iterator it = st.begin();it!=st.end();it++)
    {
        printf("%d ",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2 3 5
  • 可以发现，set 内的元素自动递增排序，且自动去除了重复元素。

set 常用函数实例解析

insert()
  • insert(x) 可以将 x 插入 set 容器中，并自动排序和去重，时间复杂度为 O(logN)O(logN)，其中 N 为 set 内的元素个数。
find()
  • find(value) 返回 set 中对应值为 value 的迭代器，时间复杂度为 O(logN)O(logN)，其中 N 为 set 内的元素个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    //注意，不支持it < st.end()的写法
    set<int>::iterator it=st.find(2);
    printf("%d",*it);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
  • 注意当 st.find(x) 函数没有找到相对应的元素时，返回的是 st.end()。
    例题：set-find与erase迭代器
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    int num,n,k;
    scanf("%d %d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num);
        st.insert(num);
    }
    set<int>::iterator it = st.find(k);
    if(it!=st.end())//注意当 `st.find(x)` 函数没有找到相对应的元素时，返回的是 `st.end()`
        st.erase(it);
    for(set<int>::iterator it=st.begin();it!=st.end();it++)
    {
        if(it!=st.begin())
            printf(" ");
        printf("%d",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
erase()
  • erase() 有两种用法：
  1. 删除单个元素；
  2. 删除一个区间内所有元素。
  • 删除单个元素有两种方法：
  • st.erase(it)，it 为所需要删除元素的迭代器。时间复杂度为 O(1)O(1)。可以结合 find() 函数来使用，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    //注意，不支持it < st.end()的写法
    set<int>::iterator it;
    st.erase(st.find(2));
    for(set<int>::iterator it = st.begin();it!=st.end();it++)
    {
        printf("%d ",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3 5
  • st.erase(value)，value 为所需要删除元素的值。时间复杂度度为 O(logN)O(logN)，其中 N 为 set 内的元素个数。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    //注意，不支持it < st.end()的写法
    //set<int>::iterator it;
    //st.erase(st.find(2));
    st.erase(2);
    for(set<int>::iterator it = st.begin();it!=st.end();it++)
    {
        printf("%d ",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3 5
  • 删除一个区间内的所有元素：
  • st.erase(first,last) 可以删除一个区间内的所有元素，其中 first 为所需要删除区间的起始迭代器，而 last 则为所需要删除区间的末尾迭代器的下一个地址，也即为删除 [first, last)。时间复杂度为 O(last−first)O(last-first)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    st.insert(1);
    st.insert(4);
    //注意，不支持it < st.end()的写法
    set<int>::iterator it;
    st.erase(st.find(3),st.end());//删除元素3至set末尾之间的元素
    for(set<int>::iterator it = st.begin();it!=st.end();it++)
    {
        printf("%d ",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1 2
size()
  • size() 用来获取 set 内的元素个数，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    st.insert(1);
    st.insert(4);
    printf("%d",st.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
5
clear()
  • clear() 用来清空 set 内的所有元素，时间复杂度为 O(N)O(N)，其中 N 为 set 内的元素个数。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <stdlib.h>
#include <set>
using namespace std;
//主函数
int main()
{
    set<int> st;
    st.insert(3);//insert(x)将x插入set中
    st.insert(5);
    st.insert(2);
    st.insert(3);
    st.insert(1);
    st.insert(4);
    st.clear();
    printf("%d",st.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
0

set 的常见用途

  1. set 最主要的作用是自动去重并按照升序排序，因此碰到需要去重但是却不方便直接开数组的情况，可以尝试用 set 解决。
  2. set 中元素是唯一的，如果需要处理不唯一的情况，则需要使用 multiset。
  3. C++11 标准中还增加了 unordered_set,以散列代替 set 内部的红黑树（一种自平衡二叉查找树）实现，使其可以用来处理只去重但不排序的需求，速度比 set 快很多！

string 的常见用法详解

  • 在 C 语言中，一般使用字符数组 char str[] 来存放字符串，但是使用字符数组有时会显得操作麻烦，而且容易因为经验不足产生错误。
  • 如果要使用 string，需要添加 string 头文件，即 #include <string>,除此之外，还需要加上 using namespace std;。

string 的定义

  • 定义 string 的方式跟基本数据类型相同，只需要在 string 后跟上变量名即可, 也可以直接给 string 类型变量赋值，示例如下：
1
2
string str;
string str = "yugin chui!";

string 中内容的访问

  1. 通过下标访问
  • 一般而言，可以直接像字符数组那样去访问 string：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <stdio.h>
#include <stdlib.h>
#include <string>
using namespace std;
//主函数
int main()
{
    string str = "yugin chui!";
    for(int i=0;i<str.length();i++)
    {
        printf("%c",str[i]);//输出"yugin chui!"
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
yugin chui!
  • 如果要读入和输出整个字符串，则只能使用 cin 和 cout：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str;
    cin >> str;
    cout << str;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 上述代码对于任意字符串输入，都会有输出同样的字符串。
  • 同样，采用 c_str() 将 string 类型转换为字符数组进行输出，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str = "yugin chui!";
    printf("%s\n",str.c_str());//采用c_str()将string类型转换为字符数组进行输出
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
yugin chui!
  1. 通过迭代器访问
  • 由于有些函数如 insert() 和 erase() 要求以迭代器为参数，因此需要学习。
  • 由于 string 不像其他 STL 容器那样需要参数，因此可以直接定义：
1
string::iterator it;
  • 这样就得到了迭代器 it，并且可以通过 *it 来访问 string 中的每一位：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str = "yugin chui!";
    for(string::iterator it = str.begin();it != str.end();it++)
    {
        printf("%c",*it);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
yugin chui!
  • 最后指出，string 和 vector 一样，支持直接对迭代器进行加减某个数字，如 str.begin()+3 的写法是可行的。

string 常用函数实例解析

  • 因为 string 的函数有很多，但是有许多函数并不常用，因此只介绍几个常用函数。
getline(cin, str);
  • 使用这个函数能够读入一整行字符串，而不会在空格处中断！示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str;
    getline(cin, str);//读入一整行字符串
    cout << str << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输入：
1
good bad
  • 输出：
1
good bad
operator+=
  • 这是 string 的加法，可以将两个 string 直接拼起来。，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "yugin chui!";
    string str2 = "Dear ";
    string str;
    str = str2 + str1;//将str2加str1,赋值给str
    cout << str << endl;
    str2 += str1;//直接将str1拼接到str2上
    cout << str2 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
Dear yugin chui!
Dear yugin chui!
compare operator
  • 两个 string 类型可以直接使用 ==、!=、<=、>=、<、>，比较规则是字典序，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "aaa";
    string str3 = "abc";
    string str4 = "xyj";
    if(str1 < str2) 
        printf("OK1\n");
    if(str1 != str3) 
        printf("OK2\n");
    if(str4 >= str3) 
        printf("OK3\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
OK1
OK2
OK3
length()/size()
  • length() 返回 string 的长度，即存放的字符数，时间复杂度为 O(1)O(1)。size() 和 length() 基本相同。
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    printf("%d %d\n",str1.length(),str1.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2 2
insert()
  • string 的 insert() 函数有许多种写法，时间复杂度 O(N)O(N)：
  1. insert(pos, string)，在 pos 号位置插入字符串 string，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bb";
    str1.insert(1,str2);
    cout << str1 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
abba
  1. insert(it,it2,it3), it 是原字符串的预插入位置，it2 和 it3 是待插字符串的首尾迭代器，用来表示字符串 [it2, it3) 将被插在 it 的位置上，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bb";
    str1.insert(str1.begin()+1,str2.begin(),str2.end());
    cout << str1 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
abba
erase()
  • erase() 有两种用法：删除单个元素、删除一个区间内的所有元素。时间复杂度均为 O(N)O(N)。
  1. 删除单个元素
  • str.erase(it) 用于删除单个元素，it 为需要删除元素的迭代器。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bb";
    str1.insert(str1.begin()+1,str2.begin(),str2.end());
    str1.erase(str1.begin()+1);
    cout << str1 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
aba
  1. 删除一个区间内的所有元素。
  • 删除一个区间内的所有元素有两种方法：
  • str.erase(first,last)，其中 first 为需要删除的区间的起始迭代器，而 last 则为需要删除的区间的末尾迭代器的下一个地址，也即为删除 [first, last)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bbc";
    str1.insert(str1.begin()+1,str2.begin(),str2.end());
    str1.erase(str1.begin()+1,str1.begin()+3);
    cout << str1 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
aca
  • str.erase(pos,length)，其中 pos 为需要开始删除的起始位置，length 为删除的字符个数，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bbc";
    str1.insert(str1.begin()+1,str2.begin(),str2.end());
    str1.erase(1,2);//删除从1号位开始的2个字符，即bb
    cout << str1 << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
aca
clear()
  • clear() 用以清空 string 中的数据，时间复杂度一般为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "aa";
    string str2 = "bbc";
    str1.insert(str1.begin()+1,str2.begin(),str2.end());
    str1.erase(1,2);//删除从1号位开始的2个字符，即bb
    str1.clear();
    cout << str1.size() << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
0
substr()
  • substr(pos, len) 返回从 pos 号位开始、长度为 len 的子串，时间复杂度为 O(len)O(len)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str1 = "Dear yugin chui!";
    cout << str1.substr(5,5) << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
yugin
string::npos
  • string::npos 是一个常数，其本身的值为 -1，但由于是 unsigned_int 类型，因此实际上也可以认为是 unsigned_int 类型的最大值。string::npos 用以作为 find 函数失配时的返回值。例如在下面的实例中可以认为 string::npos 等于 -1 或者 4294967295。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    if(string::npos==-1)
        printf("-1 is true\n"); 
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
-1 is true
find()
  • str.find(str2)，当 str2 是 str 的子串时，返回其在 str 中第一次出现的位置，如果 str2 不是 str 的子串时，那么返回 string::npos；
  • str.find(str2,pos)，从 str 的 pos 号位开始匹配 str2，返回值与上面相同。
  • 时间复杂度为 O(nm)O(nm)，其中 n 和 m 分别为 str 和 str2 的长度。
  • 示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str = "Dear yugin chui!";
    string str1 = "yugin";//能够找到
    string str2 = "yugin!";//找不到
    if(str.find(str1)!=string::npos)
        cout << str.find(str1) << endl;
    if(str.find(str2)==string::npos)
        printf("%d\n",str.find(str2));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
5
-1
replace()
  • str.replace(pos,len,str2) 把 str 从 pos 号位开始、长度为 len 的子串替换为 str2；
  • str.replace(it1,it2,str2) 把 str 的迭代器 [it1, it2) 范围的子串替换为 str2。
  • 时间复杂度为 O(str.length())O(str.length())，示例如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    string str = "Maybe you will turn around.";
    string str2 = "will not";
    string str3 = "Surely";
    cout << str.replace(10,4,str2) << endl;
    cout << str.replace(str.begin(),str.begin()+5,str3) << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
Maybe you will not turn around.
Surely you will not turn around.

string 的例题

例题：A1060 Are They Equal

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
int n;
//处理函数
string my_deal(string s,int& e)
{
    int k=0;//s的下标
    while(s.length()>0&&s[0]=='0')
    {
        s.erase(s.begin());//去掉s的前导0
    }
    if(s[0]=='.')//第一位是小数点说明s小于1
    {
        s.erase(s.begin());//去掉s的小数点
        while(s.length()>0&&s[0]=='0')
        {
            s.erase(s.begin());//去掉s的小数点后面的0
            e--;
        }
    }
    else//第一位不是小数点说明s大于1
    {
        while(k<s.length()&&s[k]!='.')//寻找小数点并且得到e
        {
            k++;
            e++;
        }
        if(k<s.length())//说明碰到了小数点
            s.erase(s.begin()+k);//去掉小数点
    }
    if(s.length()==0)//说明去除前导0后等于0
            e=0;
    int i=0;
    k=0;
    string res;
    while(i<n)//循环达到设定的精度
    {
        if(k<s.length())//只要还有数字，就往后面加
        {
            res+=s[k];
            k++;
        }
        else
            res+='0';//没有数字而且没到达精度就补0
        i++; 
    }
    return res;
}
//主函数
int main()
{
    string s1,s2,s3,s4;
    cin >> n >> s1 >> s2;
    int e1 = 0;
    int e2 = 0;
    s3 = my_deal(s1,e1);
    s4 = my_deal(s2,e2);
    if(s3==s4&&e1==e2)
    {
        cout<<"YES 0."<<s3<<"*10^"<<e1<<endl;
    }
    else
    {
        cout<<"NO 0."<<s3<<"*10^"<<e1<<" 0."<<s4<<"*10^"<<e2<<endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：string 类型能够方便处理上述题目，思路详见代码部分和《算法笔记》P 210-P 212。

map 的常见用法详解

  • map 翻译为映射，也是常用的 STL 容器。
  • map 可以将任何基本类型（包括 STL 容器）映射到任何基本类型（包括 STL 容器）。
  • 要使用 map，需要添加 map 头文件 #include <map>,除此之外，还需要加上 using namespace std;。

map 的定义

  • 单独定义一个 map：
1
map<typename1,typename2> mp;
  • map 和其他 STL 容器在定义上有点不一样，因为 map 需要确定映射前类型（键 key）和映射后类型（值 value），所有需要在 <> 内填写两个变量。
  • 其中第一个是键（key）的类型，第二个是值（value）的类型。
  • 如果是 int 型映射到 int 型，就相当于普通 int 型数组。
  • 如果是字符串（string）到整型（int）的映射，必须使用 string 而不能用 char 数组：
1
map<string,int> mp;
  • 因为 char 数组作为数组，是不能被作为键值的。
  • 同样，map 的键和值也可以是 STL 容器，例如可以将一个 set 容器映射到一个字符串：
1
map<set<int>,string> mp;

map 容器内元素访问

  • map 一般有两种访问方式：通过下标访问或通过迭代器访问。
  1. 通过下标访问
  • 和访问普通的数组是一样的，例如对一个定义为 map<char, int> mp 的 map 而言，就可以直接使用 mp['c'] 的方式来访问它对应的整数。
  • 于是，当建立映射时，就可以直接使用 mp['c']=20; 这样和普通数组一样的方式。
  • 但要注意 map 中的键（key）是唯一的：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['c']=20;
    mp['c']=30;
    printf("%d\n",mp['c']);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
30
  1. 通过迭代器访问
  • map 迭代器的定义和其他 STL 容器迭代器定义的方式相同：
1
map<typename1,typename2>::iterator it;
  • typename1 和 typename2 就是定义 map 时填写的类型，这样就得到了迭代器 it。
  • 注意 map 迭代器的使用方式和其他 STL 容器的迭代器不同，因为 map 的每一对映射都有两个 typename，这决定了必须能通过一个 it 来同时访问键和值。
  • 事实上，map 可以使用 it->first 来访问键，使用 it->second 来访问值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    for(map<char,int>::iterator it=mp.begin();it!=mp.end();it++)
    {
        printf("%c %d\n",it->first,it->second);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
a 20
b 40
c 30
  • 现象：map 会以键从小到大的顺序自动排序，即 a->b->c。
  • 原理：由于 map 内部是使用红黑树实现的（set 也是），在建立映射的过程中会自动实现从小到大的排序功能。

map 常用函数实例解析

find()
  • find(key) 返回键为 key 的映射的迭代器，时间复杂度为 O(logN)O(logN)，N 为 map 中映射的个数。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    map<char,int>::iterator it=mp.find('c');
    printf("%c %d\n",it->first,it->second);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
c 30
  • 注意如果 mp.find(key) 如果找不到元素会返回 mp.end()，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    int n,num;
    scanf("%d",&n);
    char c;
    for(int i=0;i<n;i++)
    {
        getchar();
        scanf("%c %d",&c,&num);
        mp[c]=num;
    }
    getchar();
    scanf("%c",&c);
    map<char,int>::iterator it=mp.find(c);
    if(it!=mp.end())//如果找不到返回mp.end()
        printf("%d",it->second);
    else
        printf("-1");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
erase()
  • erase() 有两种用法：删除单个元素、删除一个区间内的所有元素。
  1. 删除单个元素
  • 删除单个元素有两种方法：
  • 第一种： mp.erase(it)，it 为需要删除的元素的迭代器。时间复杂度为 O(1)O(1)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    map<char,int>::iterator it=mp.find('c');
    mp.erase(it);
    for(map<char,int>::iterator it=mp.begin();it!=mp.end();it++)
    {
        printf("%c %d\n",it->first,it->second);
    }
    // printf("%c %d\n",it->first,it->second);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
a 20
b 40
  • 第二种：mp.erase(key)，key 为删除的映射键。时间复杂度为 O(logN)O(logN)，N 为 map 中映射的个数。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    map<char,int>::iterator it=mp.find('c');
    mp.erase('c');
    for(map<char,int>::iterator it=mp.begin();it!=mp.end();it++)
    {
        printf("%c %d\n",it->first,it->second);
    }
    // printf("%c %d\n",it->first,it->second);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
a 20
b 40
  1. 删除一个区间内的所有元素
  • mp.erase(first,last)，其中 first 为需要删除的区间的起始迭代器，而 last 则为需要删除的区间的末尾迭代器的下一个地址，也即为删除左闭右开的区间 [first, last)。时间复杂度为 O(last−first)O(last-first)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    map<char,int>::iterator it=mp.find('b');
    mp.erase(it,mp.end());
    for(map<char,int>::iterator it=mp.begin();it!=mp.end();it++)
    {
        printf("%c %d\n",it->first,it->second);
    }
    // printf("%c %d\n",it->first,it->second);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
a 20
size()
  • size() 用来获得 map 中映射的对数，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    printf("%d",mp.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3
clear()
  • clear() 用来清空 map 中的所有元素，复杂度为 O(N)O(N)，其中 N 为 map 中的元素个数，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
#include <stdlib.h>
#include <map>
#include <iostream>
using namespace std;
//主函数
int main()
{
    map<char,int> mp;
    mp['a']=20;
    mp['c']=30;
    mp['b']=40;
    mp.clear();
    printf("%d",mp.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
0

queue 的常见用法详解

  • queue 翻译为队列，在 STL 中则是实现了一个先进先出的容器。

queue 的定义

  • 要使用 queue，应先添加头文件 #include <queue>，并在头文件下面添加 using namespace std;
  • queue 的定义写法和其他 STL 容器相同，typename 可以是任意基本数据类型或者容器：
1
queue<typename> name;

queue 容器内元素的访问

  • 由于队列 queue 本身就是先进先出的限制性数据结构，因此在 STL 中只能通过 front() 来访问队首元素，或者是通过 back() 来访问队尾元素。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    queue<int> q;
    for(int i=1;i<=5;i++)
    {
        q.push(i);//q.push(i);用以将i压入队列，因此依次入队1 2 3 4 5
    }
    printf("%d %d\n",q.front(),q.back());//输出结果1 5
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1 5

queue 常用函数实例解析

push()
  • push(x) 将 x 进行入队，时间复杂度为 O(1)O(1)。
front()、back()
  • front() 和 back() 可以分别获得队首元素和队尾元素,时间复杂度为 O(1)O(1)。
pop()
  • pop() 令队首元素出队，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    queue<int> q;
    for(int i=1;i<=5;i++)
    {
        q.push(i);//q.push(i);用以将i压入队列，因此依次入队1 2 3 4 5
    }
    for(int i=1;i<=3;i++)
    {
        q.pop();//出队首元素1 2 3
    }
    printf("%d %d\n",q.front(),q.back());
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
4 5
empty()
  • empty() 检测 queue 是否为空，返回 true 则空，返回 false 则非空。时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    queue<int> q;
    if(q.empty() == true)//一开始队列中没有元素，所以为空
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    for(int i=1;i<=5;i++)
    {
        q.push(i);//q.push(i);用以将i压入队列，因此依次入队1 2 3 4 5
    }
    if(q.empty() == true)
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
EMPTY!
NOT EMPTY!
size()
  • size() 返回 queue 内元素的个数，时间复杂度为 O(1)O(1)。实例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    queue<int> q;
    for(int i=1;i<=5;i++)
    {
        q.push(i);//q.push(i);用以将i压入队列，因此依次入队1 2 3 4 5
    }
    printf("%d\n",q.size());
    system("pause");    // 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
5

queue 的常见用途

  • 当需要实现广度优先搜索时，可以不用自己手动实现一个队列，而是用 queue 作为代替，以提高程序的准确性。
  • 需要注意的是，使用 front() 和 pop() 函数前，必须用 empty() 判断队列是否为空，否则可能因为队空而出现错误。
  • 延伸：STL 容器中还有两种容器与队列相关，分别是双端队列 (deque)和优先队列 (priority_queue)。
  • 双端队列 (deque)：首尾皆可插入和删除的队列；
  • 优先队列 (priority_queue)：使用堆实现的默认将当前队列最大元素置于队首的容器。

priority_queue 的常见用法详解

  • priority_queue 又称为优先队列，其底层是用堆来进行实现的。
  • 在优先队列中，队首元素一定是当前队列中优先级最高的那一个。
  • 例如在队列中有如下元素，且定义好了优先级：
1
2
3
桃子（优先级3）
梨子（优先级4）
苹果（优先级1）
  • 那么出队的顺序为梨子 (4) -> 桃子 (3) -> 苹果 (1)。
  • 当然，可以在任何时候让优先队列里面加入 (push)元素，而优先队列底层的数据结构堆 (heap)会随时调整结构，使得每次的队首元素都是优先级最大。
  • 关于上述的优先级是规定出来的。

priority_queue 的定义

  • 要使用 priority_queue，应先添加头文件 #include <queue>，并在头文件下面添加 using namespace std;
  • 其定义的写法和其他 STL 容器相同，typename 可以是任意基本数据类型或容器：
1
priority_queue<typename> name;

priority_queue 容器内元素访问

  • 和普通队列不一样的是，优先队列没有 front() 函数与 back() 函数，而只能通过 top() 函数来访问队首元素（也可以称为堆顶元素），也就是优先级最高的元素。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    priority_queue<int> q;
    q.push(1);
    q.push(2);
    q.push(4);
    q.push(3);
    printf("%d",q.top());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
4

priority_queue 常用函数实例解析

push()
  • push(x) 将令 x 入队，时间复杂度为 O(logN)O(logN)，其中 N 为当前优先队列中的元素个数。
top()
  • top() 可以获得队首元素（即堆顶元素），时间复杂度 O(1)O(1)。
pop()
  • pop() 令队首元素（即堆顶元素）出队，时间复杂度为 O(logN)O(logN)，其中 N 为当前优先队列中的元素个数，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    priority_queue<int> q;
    q.push(1);
    q.push(2);
    q.push(4);
    q.push(3);
    printf("%d\n",q.top());
    q.pop();
    printf("%d\n",q.top());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
4
3
empty()
  • empty() 检测优先队列是否为空，返回 true 则为空，返回 false 则为非空。时间复杂度为 O(1)O(1)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    priority_queue<int> q;
    if(q.empty()==true)
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    q.push(1);
    q.push(2);
    q.push(4);
    q.push(3);
    if(q.empty()==true)
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
EMPTY!
NOT EMPTY!
size()
  • size() 返回优先队列内元素的个数，时间复杂度为 O(1)O(1)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    priority_queue<int> q;
    q.push(1);
    q.push(2);
    q.push(4);
    q.push(3);
    printf("%d\n",q.size());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
4

priority_queue 内元素优先级的设置

  • 如何定义优先队列内元素的优先级是运用好优先队列的关键，下面分别介绍基本数据类型（如 int、double、char）与结构体类型的优先级设置方法。
基本数据类型的优先级设置
  • 此处的基本类型指的是 int、double、char 等可以直接使用的数据类型，优先队列对他们的优先级设置一般是数字大的优先级越高，因此队首元素就是优先队列内元素最大那个（如果是 char 型，则是字典序最大的）。对基本数据类型来说，下面两种优先队列的定义是等价的，以 int 为例：
1
2
priority_queue<int> q;
priority_queue<int , vector<int>,less<int> > q;
  • 不难发现，第二种定义方式 <> 内多出了两个参数：
  1. 一个是 vector<int>，该参数填写的是来承载底层数据结构堆 (heap)的容器，如果第一个参数是 double 型或 char 型，则此处只需要填写 vector<double> 或者 vector<char>；
  2. 另一个是 less<int>，该参数是对第一个参数的比较类，less<int> 表示数字越大优先级越大，而 greater<int> 表示数字越小优先级越大。
  • 因此，如果想让优先队列总是把最小的元素放在队首，只需进行如下定义：
1
priority_queue<int , vector<int>,greater<int> > q;
  • 示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <stdlib.h>
#include <queue>
using namespace std;
//主函数
int main()
{
    priority_queue<int , vector<int>,greater<int> > q;//数字越小优先级越大
    q.push(1);
    q.push(2);
    q.push(4);
    q.push(3);
    printf("%d\n",q.top());
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
1
结构体优先级设置
  • 本节的开头举了一个水果的例子，可以对水果的名称和价格建立一个结构体，示例如下：
1
2
3
4
struct fruit{
	string name;
	int price;
};
  • 现在希望按水果的价格高的为优先级高，就需要重载（overload）小于号"<"。重载是指对已有的运算符进行重新定义。
  • 也就是说，可以改变小于号的功能（例如把它重载为大于号的功能）。目前暂时只需要知道其写法即可：
1
2
3
4
5
6
7
8
struct fruit{
	string name;
	int price;
	friend bool operator < (fruit f1,fruit f2)
	{
		return f1.price < f2.price;
	}
};
  • 可以看到，fruit 结构体中增加了一个函数，其中 friend 是友元（自行查找资料了解）。
  • 后面的 bool operator < (fruit f1, fruit f2) 对 fruit 类型的操作符"<"进行了重载。
  • 重载大于号会编译错误，因为从数学上来说只需要重载小于号，即 f1>f2 等价于判断 f2<f1，而 f1==f2 则等价于判断 !(f1<f2)&&!(f2<f1)，函数内部为 return f1.price < f2.price;，因此重载后小于号还是小于号的作用。
  • 此时就可以直接定义 fruit 类型的优先队列，其内部就是以价格高的水果为优先级高，示例如下：
1
priority_queue<fruit> q;
  • 同理，如果想要以价格低的水果优先级高，那么只需要把 return 中的小于号改为大于号即可，示例如下：
1
2
3
4
5
6
7
8
struct fruit{
	string name;
	int price;
	friend bool operator < (fruit f1,fruit f2)
	{
		return f1.price > f2.price;
	}
};
  • 整体代码示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <stdio.h>
#include <stdlib.h>
#include <queue>
#include <string>
#include <iostream>
using namespace std;
//结构体
struct fruit{
	string name;
	int price;
	friend bool operator < (fruit f1,fruit f2)
	{
		return f1.price > f2.price;//大于号表示价格低优先级高
	}
}f1,f2,f3;
//主函数
int main()
{
    priority_queue<fruit> q;
    f1.name="桃子";
    f1.price=3;
    f2.name="梨子";
    f2.price=4;
    f3.name="苹果";
    f3.price=1;
    q.push(f1);
    q.push(f2);
    q.push(f3);
    cout << q.top().name << " " << q.top().price << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
苹果 1
  • 不难发现，此处对小于号的重载与排序函数 sort 中的 cmp 函数有些相似，它们的参数都是两个变量，函数内部都是 return 了 true 或者 false。
  • 事实上，这两者的作用确实是类似的，只不过效果看上去是“相反”的。
  • 在排序中，如果是 return f1.price > f2.price;，那么则是按照价格从高到低排序。
  • 在优先队列中，则是把价格低的放到队首。原因在于，优先队列本身默认的规则就是优先级高的放队首，因此把小于号重载为大于号的功能时只是把这个规则反向了一下。
  • 最后，只需要记住优先队列的这个函数与 sort 中的 cmp 函数的效果相反的即可。
  • 把优先队列的比较函数放外面：只需要把 friend 去掉，把小于号改成一对小括号，然后把重载的函数写在结构体的外面，同时将其用 struct 包装起来，示例如下：
1
2
3
4
5
6
struct cmp{
	bool operator() (fruit f1,fruit f2)
	{
		return f1.price > f2.price;
	}
};
  • 在这种情况下，需要用之前讲解的第二种定义方式来定义优先队列：
1
priority_queue<fruit , vector<fruit> , cmp> q;
  • 可以看到，此处只是把 greater<> 部分换成了 cmp。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
#include <stdlib.h>
#include <queue>
#include <string>
#include <iostream>
using namespace std;
//结构体
struct fruit{
	string name;
	int price;
}f1,f2,f3;
struct cmp{
	bool operator() (fruit f1,fruit f2)
	{
		return f1.price > f2.price;
	}
};
//主函数
int main()
{
    priority_queue<fruit , vector<fruit> , cmp> q;
    f1.name="桃子";
    f1.price=3;
    f2.name="梨子";
    f2.price=4;
    f3.name="苹果";
    f3.price=1;
    q.push(f1);
    q.push(f2);
    q.push(f3);
    cout << q.top().name << " " << q.top().price << endl;
    //q.pop();
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
苹果 1
  • 与此同时，我们应该联想到，即便是基本数据类型或者其它 STL 容器（例如 set），也可以通过同样的方式来定义优先级。
  • 最后指出，如果结构体内的数据较为庞大（例如出现了字符串或者数组），建议使用引用来提高效率，此时比较类的参数中需要加上 "const" 和 "&"，示例如下：
1
2
3
4
5
6
7
8
struct fruit{
	string name;
	int price;
	friend bool operator < (const fruit &f1,const fruit &f2)
	{
		return f1.price > f2.price;//大于号表示价格低优先级高
	}
};
  • 以及：
1
2
3
4
5
6
struct cmp{
	bool operator() (const fruit &f1,const fruit &f2)
	{
		return f1.price > f2.price;
	}
};

priority_queue 的常见用途

  • priority_queue 可以解决一些贪心问题，也可以对 Dijkstra 算法进行优化（因为优先队列的本质是堆）。
  • 需要注意的是，使用 top() 函数前，必须用 empty() 判断优先队列是否为空，否则可能因为队列空而出现错误！

stack 的常见用法详解

  • stack 翻译为栈，是 STL 中实现的一个后进先出的容器。

stack 的定义

  • 要使用 stack，应该先添加头文件 #include <stack>，并在头文件下面加上 using namespace std;
  • 其定义的写法和其他 STL 容器相同，typename 可以是任意基本数据类型或容器：
1
stack<typename> name;

stack 容器内元素的访问

  • 由于栈（stack）本身就是一种后进先出的数据结构，在 STL 的 stack 只能通过 top() 来访问栈顶元素。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    stack<int> st;
    for(int i=1;i<=5;i++)
    {
        st.push(i);
    }
    printf("%d\n",st.top());//st.top()取栈顶元素
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
5

stack 常用函数实例解析

push()
  • push(x) 将 x 入栈，时间复杂度为 O(1)O(1)。
top()
  • top() 获得栈顶元素，时间复杂度为 O(1)O(1)。
pop()
  • pop() 用以弹出栈顶元素，时间复杂度为 O(1)O(1)。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    stack<int> st;
    for(int i=1;i<=5;i++)
    {
        st.push(i);
    }
    for(int i=1;i<=3;i++)
    {
        st.pop();
    }
    printf("%d\n",st.top());//st.top()取栈顶元素
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
empty()
  • empty() 可以检测 stack 内是否为空，返回 true 则为空，返回 false 则为非空。时间复杂度为 O(1)O(1)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    stack<int> st;
    if(st.empty()==true)
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    for(int i=1;i<=5;i++)
    {
        st.push(i);
    }
    if(st.empty()==true)
    {
        printf("EMPTY!\n");
    }
    else
    {
        printf("NOT EMPTY!\n");
    }
    //printf("%d\n",st.top());//st.top()取栈顶元素
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
EMPTY!
NOT EMPTY!
size()
  • size() 返回 stack 内元素个数，时间复杂度为 O(1)O(1)，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
using namespace std;
//主函数
int main()
{
    stack<int> st;
    for(int i=1;i<=5;i++)
    {
        st.push(i);
    }
    printf("%d\n",st.size());//st.top()取栈顶元素
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
5

stack 的常见用途

  • stack 用来模拟实现一些递归，防止程序对栈内存的限制而导致程序运行出错。
  • 一般来说，程序的栈内存空间很小，对有些题目来说，如果用普通的函数进行递归，一旦递归层数过深（不同机器不同，约几千至几万层），则会导致程序运行崩溃。
  • 如果用栈来模拟递归算法的实现，则可以避免这一问题，不过应用较少。

pair 的常见用法详解

  • pair 是一个很实用的容器，当想要将两个元素绑在一起作为一个合成元素，又不想因此定义结构体时，使用 pair 可以很方便地作为一个替代品。
  • 也就是说，pair 实际上可以看作一个内部有两个元素的结构体，且这两个元素是可以指定的，如下面结构体的短代码所示：
1
2
3
4
5
struct pair
{
	typename1 first;
	typename2 second;
};

pair 的定义

  • 要使用 pair，应先添加头文件 #include <utility>，并在头文件下面加上 using namespace std;
  • 注意，由于 map 的内部涉及 pair，因此添加 map 头文件时会自动添加 utility 头文件。
  • pair 有两个参数，分别对于 first 和 second 的数据类型，它们可以是任意基本数据类型或容器，示例如下：
1
2
pair<typename1 , typename2> name;
pair<string , int> p;
  • 如果想在定义 pair 时进行初始化，只需要跟上一个小括号，里面填写两个想要初始化的元素即可：
1
pair<string , int> p("yugin!",8);
  • 而如果想要在代码中临时构建一个 pair，有如下两种方法：
  1. 将类型定义在前面，后面用小括号内两个元素的方式：
1
pair<string , int>("yugin!",8);
  1. 使用自带的 make_pair 函数：
1
make_pair("yugin!",8);
  • 关于这两种用法见下述例子。

pair 中元素的访问

  • pair 中只有两个元素，分别是 first 和 second，只需要按照正常结构体的方式去访问即可，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
using namespace std;
//主函数
int main()
{
    pair<string , int> p;
    p.first = "yugin!";
    p.second = 5;
    cout << p.first << " " << p.second << endl;
    p = make_pair("chui yugin!",88);
    cout << p.first << " " << p.second << endl;
    p = pair<string , int>("chui yugin yep!",888);
    cout << p.first << " " << p.second << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
yugin! 5
chui yugin! 88
chui yugin yep! 888

pair 常用函数实例解析

比较操作数
  • 两个 pair 类型数据可以直接使用 ==、!=、<、<=、>、>= 比较大小，比较规则是先以 first 的大小作为标准，只有当 first 相等时才去判断 second 的大小。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
using namespace std;
//主函数
int main()
{
    pair<int , int> p1(5,10);
    pair<int , int> p2(5,15);
    pair<int , int> p3(10,5);
    if(p1 < p3)
        printf("p1 < p3\n");
    if(p1 <= p3)
        printf("p1 <= p3\n");
    if(p1 < p2)
        printf("p1 < p2\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
p1 < p3
p1 <= p3
p1 < p2

pair 的常见用途

  • 关于 pair 有两个比较常见的例子：
  1. 用来代替二元结构体及其构造函数，可以节省编码时间。
  2. 作为 map 的键值对来进行插入，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
using namespace std;
//主函数
int main()
{
    map<string,int> mp;
    mp.insert(make_pair("yugin!",88));
    mp.insert(pair<string,int>("Mr.yugin!",8));
    for(map<string,int>::iterator it = mp.begin();it!=mp.end();it++)
    {
        cout << it->first << " " << it->second << endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
Mr.yugin! 8
yugin! 88

algorithm 头文件下的常用函数

  • 使用 #include <algorithm> 头文件，需要在头文件下加一行using namespace std;

max()、min()和 abs()

  • max(x,y) 和 min(x,y) 分别返回 x 和 y 中的最大值和最小值，且参数必须是两个（可以是浮点数）。
  • 如果想要返回 x、y、z 三个数的最大值, 可以使用 max(x,max(y,z)) 写法。
  • abs(x) 返回 x 的绝对值。
  • 注意：x 必须是整型，浮点型的绝对值用 #include <math> 头文件下的 fabs 函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int x = 1,y = -2;
    printf("%d %d\n",max(x,y),min(x,y));
    printf("%d %d\n",abs(x),abs(y));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
1 -2
1 2

swap()

  • swap(x,y) 用来交换 x 和 y 的值，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int x = 1,y = -2;
    swap(x,y);
    printf("%d %d\n",x,y);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
-2 1

reverse()

  • reverse(it,it2) 可以将数组指针在 [it, it2) 之间的元素或容器的迭代器在 [it, it2) 范围内的元素进行反转。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int a[10] = {10,11,12,13,14,15};
    reverse(a,a+4);//将a[0]~a[3]反转
    for(int i=0;i<6;i++)
    {
        printf("%d ",a[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
13 12 11 10 14 15
  • 如果是对容器中的元素（例如 string 字符串）进行反转，结果也一样：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    string str = "abcdef";
    reverse(str.begin(),str.begin()+4);//将str[0]~str[3]反转
    for(int i=0;i<str.length();i++)
    {
        printf("%c",str[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
dcbaef

next_permutation()

  • next_permutation() 给出一个序列在全排序的下一个序列。
  • 例如当 n==3 时的全排列为：
1
2
3
4
5
6
123
132
213
231
312
321
  • 这样 231 的下一个序列就是 312，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int a[10] = {1,2,3};
    //a[0]~a[2]之间的序列需要求解next_permutation()
    do
    {
        printf("%d%d%d\n",a[0],a[1],a[2]);
    }while(next_permutation(a,a+3));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
4
5
6
123
132
213
231
312
321
  • 在上述代码中，使用循环是因为 next_permutation() 在已经到达全排列的最后一个时会返回 false，这样会方便退出循环。
  • 而使用 do...while 语句而不使用 while 语句是因为序列 123 本身也需要输出，如果使用 while 语句会直接跳到下一个序列再输出，这样结果会少一个 123。

fill()

  • fill() 可以把数组或容器中的某一段区间赋为某个相同的值。
  • 和 memset 不同，这里的赋值可以是数组类型对应范围中的任意值。示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int a[10] = {1,2,3,4,5};
    fill(a,a+5,888);//将a[0]~a[4]均赋值为888
    for(int i=0;i<5;i++)
    {
        printf("%d ",a[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
888 888 888 888 888
  • 对于二维数组的使用，示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
using namespace std;
//主函数
int main()
{
    int n=3,m=5;
    int a[n][m];
    int k;
    scanf("%d",&k);
    fill(a[0], a[0] + n * m, k);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            printf("%d", a[i][j]);
            if (j < m - 1) {
                printf(" ");
            } else {
                printf("\n");
            }
        }
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

sort()

  • 由于排序题中大部分只需要得到排序的最终结果，而不需要去写完整的排序过程，因此推荐采用 C++ 中的 sort() 函数进行处理。
如何使用 sort ()函数排序
  • sort() 函数的使用必须加上头文件 #include <algorithm> 和 using namespace std;，其使用方式如下：
1
sort(首元素地址(必填),尾元素地址的下一个地址(必填),比较函数(非必填));
如何实现比较函数 cmp
基本数据类型数组的排序
  • 若比较函数不填，则默认按照从小到大的顺序排序。
  • 例如：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
//主函数
int main(){
    int a[5]={1,2,3,4,5};
    sort(a,a+5);
    for(int i=0;i<5;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}
  • 输出：
1
1 2 3 4 5
  • 如果想要实现从大到小来排序，则需要编写 cmp (比较函数)：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
bool cmp(int a,int b)
{
    return a>b;//可以理解为当a>b时，把a放在b前面
}
//主函数
int main(){
    int a[5]={1,2,3,4,5};
    sort(a,a+5,cmp);
    for(int i=0;i<5;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}
  • 输出：
1
5 4 3 2 1
  • 记忆方法：
    • 数据“从小到大”就用 “<”，因为 a<b 是左小右大
    • 数据“从大到小”就用 “>”，因为 a>b 是左大右小
结构体数组排序
  • 一级排序
1
2
3
4
bool cmp(node a,node b)
{
	return a.x>b.x;
}
  • 二级排序
1
2
3
4
5
6
7
8
9
10
11
bool cmp(node a,node b)
{
	if(a.x!=b.x)
	{
		return a.x>b.x;
	}
	else
	{
		return a.y<b.y;
	}
}
容器排序
  • 在 STL 标准容器中，只有 vector、string、deque 是可以使用 sort 的。因为像 set 和 map 这样的容器是采用红黑树实现的，元素本身有序，故不允许 sort 排序。
  • 下面以 vector 为例：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//比较函数
bool cmp(int a,int b)//vector中的元素为int型
{
    return a>b;//从大到小
}
//主函数
int main()
{
    vector<int> vi;
    vi.push_back(2);
    vi.push_back(3);
    vi.push_back(1);
    sort(vi.begin(),vi.end(),cmp);
    for(int i=0;i<3;i++)
    {
        printf("%d ",vi[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3 2 1
  • 以 string 为例：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//主函数
int main()
{
    string str[3] = {"bbbb","cc","aaa"};
    sort(str,str+3);//将string型数组按照字典序从小到大排序
    for(int i=0;i<3;i++)
    {
        cout<<str[i]<<endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
aaa
bbbb
cc
  • 在上述例子中，如果需要按照字符串长度从小到大排序，可以见如下示例：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//比较函数
bool cmp(string a,string b)//vector中的元素为int型
{
    return a.length()<b.length();//从小到大
}
//主函数
int main()
{
    string str[3] = {"bbbb","cc","aaa"};
    sort(str,str+3,cmp);//将string型数组按照字典序从小到大排序
    for(int i=0;i<3;i++)
    {
        cout<<str[i]<<endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
cc
aaa
bbbb

lower_bound()和 upper_bound()

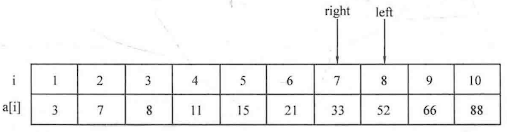
  • lower_bound() 和 upper_bound() 需要用在一个有序数组或容器中。
  • lower_bound(first,last,val) 用来寻找在数组或容器的 [first, last) 范围内第一个值大于等于 val 元素的位置，如果是数组，则返回该位置的指针；如果是容器，则返回该位置的迭代器。
  • upper_bound(first,last,val) 用来寻找在数组或容器的 [first, last) 范围内第一个值大于 val 元素的位置，如果是数组，则返回该位置的指针；如果是容器，则返回该位置的迭代器。
  • 显然，如果数组或容器中没有需要寻找的元素，则 lower_bound() 和 upper_bound() 均返回可以插入该元素的位置的指针或迭代器（即假设存在该元素时，该元素应当在的位置）。
  • lower_bound() 和 upper_bound() 的复杂度均为 O(log(last−first))O(log(last-first))。
  • 示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//主函数
int main()
{
    int a[10] = {1,2,2,3,3,3,5,5,5,5};
    //寻找-1
    int *lowerPos = lower_bound(a,a+10,-1);
    int *upperPos = upper_bound(a,a+10,-1);
    printf("%d %d\n",lowerPos-a,upperPos-a);
    //寻找1
    lowerPos = lower_bound(a,a+10,1);
    upperPos = upper_bound(a,a+10,1);
    printf("%d %d\n",lowerPos-a,upperPos-a);
    //寻找3
    lowerPos = lower_bound(a,a+10,3);
    upperPos = upper_bound(a,a+10,3);
    printf("%d %d\n",lowerPos-a,upperPos-a);
    //寻找4
    lowerPos = lower_bound(a,a+10,4);
    upperPos = upper_bound(a,a+10,4);
    printf("%d %d\n",lowerPos-a,upperPos-a);
    //寻找6
    lowerPos = lower_bound(a,a+10,6);
    upperPos = upper_bound(a,a+10,6);
    printf("%d %d\n",lowerPos-a,upperPos-a);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
3
4
5
0 0
0 1
3 6
6 6
10 10
  • 显然，如果只是想获得欲查元素的下标，就可以不使用临时指针，而直接令返回值减去数组首地址即可：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//主函数
int main()
{
    int a[10] = {1,2,2,3,3,3,5,5,5,5};
    //寻找3
    printf("%d %d\n",lower_bound(a,a+10,3)-a,upper_bound(a,a+10,3)-a);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3 6

算法初步

排序

  • 本章先介绍两种基础的排序算法：选择排序与插入排序。

选择排序

  • 简单选择排序：对于一个序列A中的元素A[1]-A[n]，令i从1到n枚举，进行n趟操作，每趟从待排序部分[i,n]中选择最小元素，令其与待排序部分的第一个元素A[i]进行交换，这样元素A[i]就会与当前有序区间[1,i-1]形成新的有序区间[1,i]。

  • 总共需要进行n趟操作(1<=i<=n)，每趟操作选出待排序部分[i,n]中的最小元素，令其与A[i]交换。总复杂度为O(n2)O(n^2)

  • 实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//选择排序函数
void select_sort(int list[],int num)
{
    int min_num,k,temp;
    for(int i=0;i<num;i++)
    {
        min_num=list[i];
        k=i;
        for(int j=i;j<num;j++)
        {
            if(list[j]<min_num)
            {
                min_num = list[j];
                k=j;
            }
        }
        temp=list[i];
        list[i]=min_num;
        list[k]=temp;
    }
}

插入排序

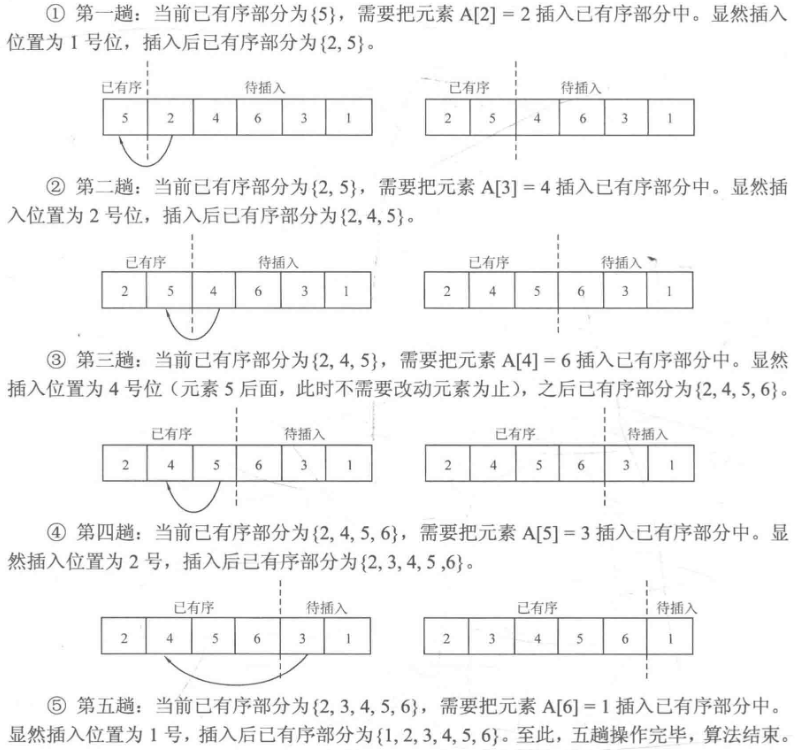
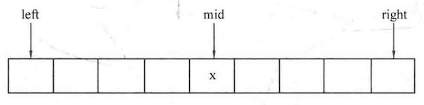
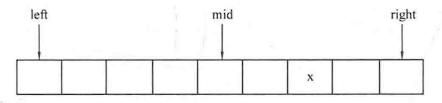
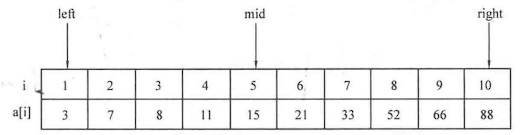
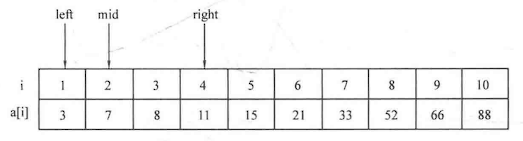
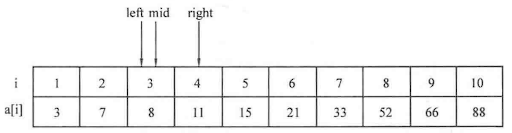
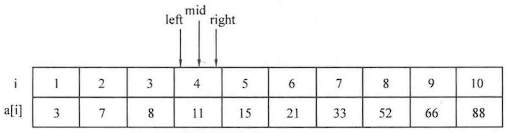
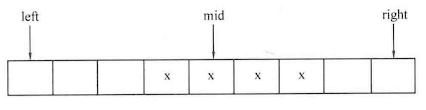
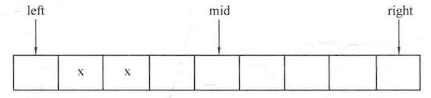
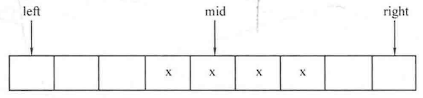
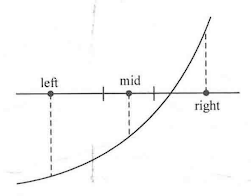
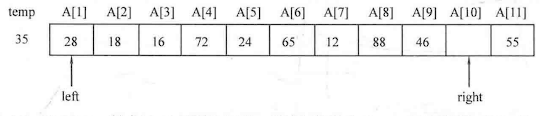
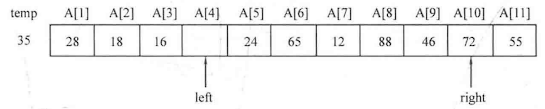
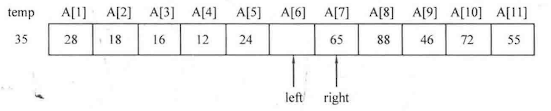
  • 直接插入排序：对于一个序列A中的元素A[1]-A[n]，令i从1到n-1枚举，进行n-1趟操作。假设某一趟时，序列A的前i-1个元素A[1]-A[i-1]已经有序，而范围[i,n]还未有序，那么该趟从范围[1,i-1]中寻找某个位置j，使得将A[i]插入位置j后(此时A[j]-A[i-1]会后移一位至A[j+1]-A[i])，范围[1,i]有序。
  • 思想如下图所示：


  • 实现代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//插入排序函数
void insert_sort(int list[],int num)
{
    int temp,j;
    for(int i=1;i<num;i++)//进行n-1趟
    {
        temp=list[i];
        j=i;
        while(j>0&&temp<list[j-1])//只要temp小于前一个元素list[j-1]
        {
            list[j]=list[j-1];//把list[j-1]移到list[j]
            j--;
        }
        list[j]=temp;//插入位置为j
    }
}

排序题与sort函数的应用

  • 由于排序题中大部分只需要得到排序的最终结果，而不需要去写完整的排序过程，因此推荐采用C++中的sort()函数进行处理。
如何使用sort()函数排序
  • sort()函数的使用必须加上头文件#include <algorithm>和using namespace std;，其使用方式如下：
1
sort(首元素地址(必填),尾元素地址的下一个地址(必填),比较函数(非必填));
如何实现比较函数cmp
基本数据类型数组的排序
  • 若比较函数不填，则默认按照从小到大的顺序排序。
  • 例如：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
//主函数
int main(){
    int a[5]={1,2,3,4,5};
    sort(a,a+5);
    for(int i=0;i<5;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}
  • 输出：
1
1 2 3 4 5
  • 如果想要实现从大到小来排序，则需要编写cmp(比较函数)：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
bool cmp(int a,int b)
{
    return a>b;//可以理解为当a>b时，把a放在b前面
}
//主函数
int main(){
    int a[5]={1,2,3,4,5};
    sort(a,a+5,cmp);
    for(int i=0;i<5;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}
  • 输出：
1
5 4 3 2 1
  • 记忆方法：
    • 数据“从小到大”就用“<”，因为a<b是左小右大
    • 数据“从大到小”就用“>”，因为a>b是左大右小
结构体数组排序
  • 一级排序
1
2
3
4
bool cmp(node a,node b)
{
	return a.x>b.x;
}
  • 二级排序
1
2
3
4
5
6
7
8
9
10
11
bool cmp(node a,node b)
{
	if(a.x!=b.x)
	{
		return a.x>b.x;
	}
	else
	{
		return a.y<b.y;
	}
}

例题：考场排名

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1100;
//结构体
struct stu{
    char name[20];
    int score;
    int kaochang;
    int paiming;
};
//比较函数
bool cmp1(stu a,stu b)
{
    return a.score>b.score;
}
bool cmp2(stu a,stu b)
{
        return strcmp(a.name,b.name)<0;
}
//主函数
int main(){
    int n,num_kaochang,sum=0,num[15];
    scanf("%d",&n);
    stu stu[MAXN];
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num_kaochang);
        for(int k=sum;k<num_kaochang+sum;k++)
        {
            scanf("%s",stu[k].name);
            scanf("%d",&stu[k].score);
            stu[k].kaochang=i;
        }
        num[i]=num_kaochang;
        sort(stu+sum,stu+sum+num_kaochang, cmp1);
        stu[sum].paiming=1;
        for(int m=sum;m<sum+num_kaochang;m++)
        {
            if(stu[m].score==stu[m-1].score)
            {
                stu[m].paiming=stu[m-1].paiming;
            }
            else
            {
                stu[m].paiming=m+1-sum;//局部排名数值要减去sum
            }
        }
        sum+=num_kaochang;
    }
    sort(stu,stu+sum, cmp2);
    for(int i=0;i<sum;i++)
    {
        printf("%s %d %d\n",stu[i].name,stu[i].score,stu[i].paiming);
    }
    return 0;
}
  • 总结：注意一下字符串数组的比较函数的写法，以及这道题目局部（考场）排名的大小需要减去sum值。

例题：A1025 PAT Ranking

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 51000;
//结构体
struct stu{
    char name[20];
    int score;
    int kaochang;
    int paiming;
    int final_rank;
};
//比较函数
bool cmp1(stu a,stu b)
{
    return a.score>b.score;
}
bool cmp2(stu a,stu b)
{
    if(a.final_rank==b.final_rank)
    {
        return strcmp(a.name,b.name)<0;
    }
    else
    {
        return a.final_rank<b.final_rank;
    }
}
//主函数
int main(){
    int n,num_kaochang,sum=0;
    scanf("%d",&n);
    stu stu[MAXN];
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num_kaochang);
        for(int k=sum;k<num_kaochang+sum;k++)
        {
            scanf("%s",stu[k].name);
            scanf("%d",&stu[k].score);
            stu[k].kaochang=i+1;
        }
        //排local_rank
        sort(stu+sum,stu+sum+num_kaochang, cmp1);
        stu[sum].paiming=1;
        for(int m=sum;m<sum+num_kaochang;m++)
        {
            if(stu[m].score==stu[m-1].score)
            {
                stu[m].paiming=stu[m-1].paiming;
            }
            else
            {
                stu[m].paiming=m+1-sum;//局部排名数值要减去sum
            }
        }
        sum+=num_kaochang;
    }
    //按照成绩重新进行排名，不区分考场
    sort(stu,stu+sum, cmp1);
    stu[0].final_rank=1;
    for(int m=1;m<sum;m++)
    {
        if(stu[m].score==stu[m-1].score)
        {
            stu[m].final_rank=stu[m-1].final_rank;
        }
        else
        {
            stu[m].final_rank=m+1;
        }
    }
    //按照字典序排输出
    sort(stu,stu+sum, cmp2);
    //输出
    printf("%d\n",sum);
    for(int i=0;i<sum;i++)
    {
        printf("%s %d %d %d\n",stu[i].name,stu[i].final_rank,stu[i].kaochang,stu[i].paiming);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：可以在结构体数组中把对应要输出的内容提前定义，这样在运算赋值之后就可以直接输出。

散列

散列的定义和整数散列

  • 散列(Hash)，简单而言，就是将元素通过一个函数转换为整数，使得该整数可以尽量唯一地代表这个元素。

  • 其中把这个转换函数称为散列函数H，也就是说，如果元素在转换前为Key，那么转换后为一个整数H(Key)。

  • 常用的散列函数：直接定址法、平方取中法、除留余数法等…

  • 如果两个不同的元素Key1和Key2，它们的Hash值H(Key1)和H(Key2)是相同的话，就称为冲突。

  • 解决冲突的主要办法有：线性探查法、平方探查法、链地址法(拉链法)

  • 其中第一种和第二种都计算了新的Hash值，称为开放定址法

  • 散列表的特点是能够使用空间来换取时间

字符串Hash初步

  • 字符串Hash是指将一个字符串Str映射成一个整数，使得该整数可以尽可能唯一地代表字符串Str。
  • 为了讨论问题方便，先假设字符串均有大写字母'A'-'Z'组成，在此基础上，不妨把大写字母'A'-'Z'看成0-25。
  • 由此便可以将字符串映射为整数(注意：转换成整数最大为 261en−126^{1en}-1 其中 len 为字符串长度)
  • 代码如下：
1
2
3
4
5
6
7
8
9
int HashFunc(char Str[],int len)//Hash函数，将字符串Str转换为整数
{
	int id=0;
	for(int i=0;i<len;i++)
	{
		id=id*26+(Str[i]-'A');//转换为整数
	}
	return id;
}

  • 如果字符串中出现了小写字母，那么可以把大写字母'A'-'Z'看成0-25，把小写字母'a'-'z'看成26-51，其余相同。

  • 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int HashFunc(char Str[],int len)//Hash函数，将字符串Str转换为整数
{
	int id=0;
	for(int i=0;i<len;i++)
	{
		if(Str[i]>='A'&&Str[i]<='Z')
		{
			id=id*52+(Str[i]-'A');//转换为整数
		}
		else if(Str[i]>='a'&&Str[i]<='z')
		{
			id=id*52+(Str[i]-'a')+26;//转换为整数
		}
	}
	return id;
}
  • 再增加不同的字符代码编写方式同理；

例题：字符串出现次数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1010;
char str[MAXN][5];
int hashTable[26*26*26+10]={0};
//字符串转Hash函数
int HashFunc(char s[],int len)
{
    int id=0;
    for(int i=0;i<len;i++)
    {
        id=id*26+(s[i]-'A');
    }
    return id;
}
//主函数
int main(){
    int n,m;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%s",str[i]);
        hashTable[HashFunc(str[i],3)]++;
    }
    scanf("%d",&m);
    for(int i=0;i<m;i++)
    {
        scanf("%s",str[i]);
        printf("%d",hashTable[HashFunc(str[i],3)]);
        if(i!=m-1)
        {
            printf(" ");
        }
    }
    return 0;
}
  • 总结：该题直接给出字符串散列的处理方法！重点掌握字符串转整数函数的编写和应用。

例题：2-SUM-hash

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1000001;
int num[MAXN]={0},hashTable[MAXN]={0};
//主函数
int main(){
    int n,k;
    scanf("%d %d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num[i]);
        hashTable[num[i]]++;
    }
    int ans=0;
    for(int i=0;i<n;i++)
    {
        if(k-num[i]>=0&&hashTable[k-num[i]])
        {
            ans++;
        }
    }
    printf("%d",ans/2);
    return 0;
}
  • 总结：这道题目的巧妙之处在于通过用求和值k减去a后的值b是否还在哈希表中来判断是否满足条件。这样巧妙利用了空间换时间的思想，只用一次循环即可完成！最后注意最终结果需要再÷2！

递归

分治

  • 分治->“分而治之”
  • 分治法将原问题划分成若干个规模较小而结构与原问题相同或者相似的子问题，然后分别解决这些子问题，最后合并子问题的解，即可得到原问题的解。
    • 分解：将原问题划分成若干个规模较小而结构与原问题相同或者相似的子问题；
    • 解决：递归求解所有子问题。如果存在子问题的规模足够小就可以直接解决；
    • 合并：将子问题的解合并为原问题的解。
  • 分治法分解成的子问题应该是相互独立的、没有交叉的。
  • 分治法作为一种算法思想，既可以使用递归的手段去实现，也可以通过非递归的手段去实现。

递归

  • 递归在于反复调用自身函数，但是每次把问题范围缩小，直到范围缩小到可以直接得到边界数据的结果，然后再在返回的路上求出对应的解。
  • 递归很适合用来实现分治思想；
  • 递归的逻辑中一般有两个重要概念：
    • 递归边界
    • 递归式（或称递归调用）
  • 递归式是将原问题分解为若干个子问题的手段；
  • 递归边界是分解的尽头。
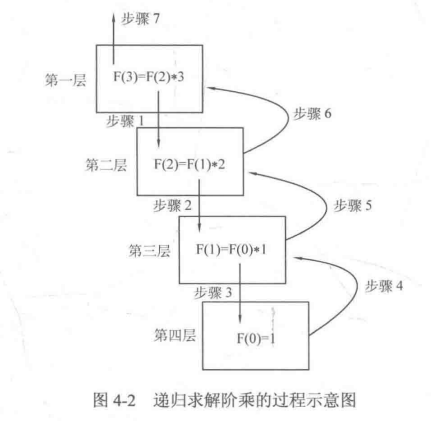
  • 例题->递归求解n的阶乘：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <string.h>
using namespace std;
//函数
int F(int n)
{
    if(n==0) return 1;//递归边界
    else return F(n-1)*n;//递归式
}
//主函数
int main(){
    int a=3;
    printf("%d",F(a));
    return 0;
}
  • 输出：
1
6
  • 其实现过程如下：

  • 例题->递归求解斐波那契数列的第n项：
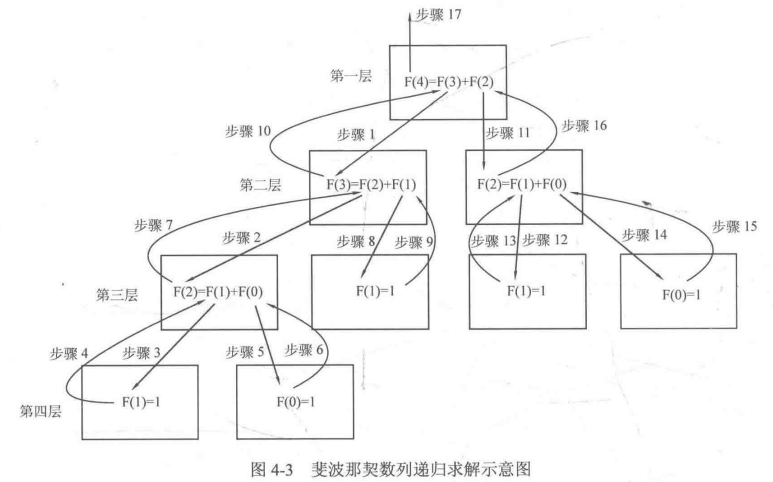
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
//斐波那契数列递归函数（输出第n项的值）
int F(int n)
{
    if(n==0||n==1)
        return 1;//递归边界
    else return F(n-1)+F(n-2);//递归式
}
//主函数
int main(){
    int n=4;
    printf("%d",F(n));
    return 0;
}
  • 输出：
1
5
  • 其实现过程如下：

  • 例题->全排列问题：

  • 思路：
  • 从递归的角度考虑，把问题描述成：“输出1 - n这n个整数的全排列”，那么它就可以分解成若干个子问题：
    • 输出以1开头的全排列：(1,2,3)、(1,3,2);
    • 输出以2开头的全排列：(2,1,3)、(2,3,1);
    • 输出以3开头的全排列：(3,1,2)、(3,2,1);
    • 以此类推…直到第n个。
  • 由此，不妨设定一个数组p[MAXN]用于存放当前的排列;
  • 再设定一个散列数组bool HashTable[MAXN]={false};用于指示当前元素k是否在数组p中，
    • 如果已经存在于p中时HashTable[k]=true;
    • 如果不存在于p中时HashTable[k]=false;
  • 因为要按照字典序对全排列进行输出，我们需要按顺序往数组p中第1位到n位中填入数字。
  • 不妨假设我们当前已经填好了p[1]-p[index]部分的数字，下一步需要填P[index+1]这个位置的数字。
  • 显然需要从1-n中枚举有哪些数字还没有在p[1]-p[index]部分，即满足HashTable[k]==false这个条件，那么就将该数字填入p[index]中。
  • 然后将HashTable[k]=true，表示k这个数据已经填入了数组p中。
  • 然后可以像上述步骤一样处理index+2的数据，即p[1]-p[index+1]已经填好，即进行递归->重复执行Full_permutation(index+1);直到后续递归完成。
  • 当递归完成后，需要再将HashTable[k]=false，以便后续能够继续使用这个数据。
  • 最后递归边界显然是当index到达n+1时，说明数组p中的第1 - n位都已经填好了，只需要按顺序进行输出即可。
  • 下面是当n=3时候的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
//全排列递归函数变量定义
const  int MAXN = 20;
int n;//输出index-n的全排列
int p[MAXN];
bool HashTable[MAXN]={false};
//全排列递归函数
void Full_permutation(int index)
{
    //递归边界
    if(index==n+1)
    {
        for(int i=1;i<=n;i++)
        {
            printf("%d",p[i]);
        }
        printf("\n");
        return ;
    }
    //递归式
    for(int k=1;k<=n;k++)
    {
        if(!HashTable[k])//HashTable[k]==false->说明该元素还没有被用上
        {
            p[index]=k;//处理这一种情况
            HashTable[k] = true;//到这里说明假设1到index已经排好
            //递归进入函数再排index+1之后的部分
            Full_permutation(index+1);
            //递归返回结束后循环还没有结束，继续处理下一循环的问题
            HashTable[k] = false;//已经处理完p[index]=k;这一种情况，还原状态
        }
    }
}
//主函数
int main(){
    n=3;
    Full_permutation(1);//index从1开始
    return 0;
}
  • 输出：
1
2
3
4
5
6
123
132
213
231
312
321
  • 例题->n皇后问题：

  • 思路：

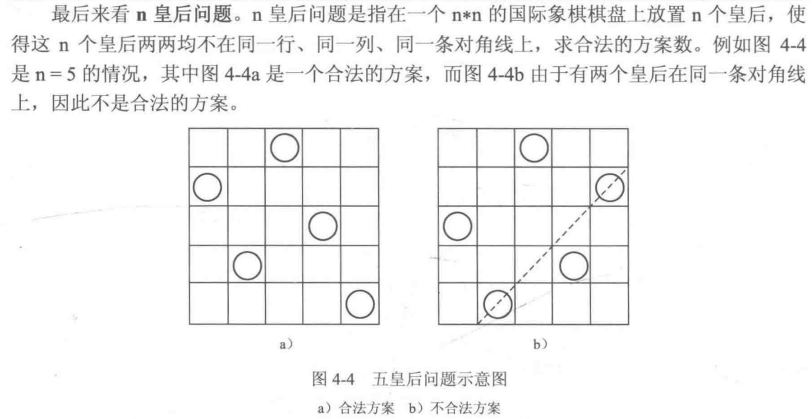
  • 根据题意很容易想到每行和每列只能放置一个皇后，只需要将n列或者n行皇后的位置写出即可代表一种情况。

  • 例如将皇后的行号写出，图4-4a的序号为24135，图4-4b的序号为35142。

  • 按照这个思路只需要枚举1 - n的所有排列，并且查看每个排列对应的放置方案是否合法，统计合法的方案即可，总共只有n!个排列。

  • 可以参考全排列的方法，生成一段排列序号后，在递归边界判断序号是否合法，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
//n皇后函数变量定义
const  int MAXN = 20;
int n;//输出index-n的全排列
int p[MAXN];
bool HashTable[MAXN]={false};
int my_count = 0;//记录合法的皇后排列个数
//n皇后问题递归函数
void n_queens(int index)
{
    //递归边界
    if(index==n+1)
    {
        bool flag = true;
        for(int i=1;i<n;i++)
        {
            for(int j=i+1;j<=n;j++)
            {
                if(abs(i-j)==abs(p[i]-p[j]))
                {
                    flag = false;
                    break;
                }
            }
        }
        if(flag)
        {
            my_count++;
        }
        return ;
    }
    //递归式
    for(int k=1;k<=n;k++)
    {
        if(!HashTable[k])//HashTable[k]==false->说明该元素还没有被用上
        {
            p[index]=k;//处理这一种情况
            HashTable[k] = true;//到这里说明假设1到index已经排好
            //递归进入函数再排index+1之后的部分
            n_queens(index+1);
            //递归返回结束后循环还没有结束，继续处理下一循环的问题
            HashTable[k] = false;//已经处理完p[index]=k;这一种情况，还原状态
        }
    }
}
//主函数
int main(){
    n=8;
    n_queens(1);//index从1开始
    printf("%d",my_count);
    return 0;
}
  • 输出：
1
92
  • 总结：
  • 上述方法在序列完成时再判断该序列是否合法，未使用任何优化方法，称为暴力法。
  • 事实上，可以发现当已经放置了一部分皇后以后（对应生成了排列的一部分），如果后续皇后无论怎么放置都冲突的话，即可中止递归了。
  • 一般而言，如果在到达递归边界前的某层，由于一些事实导致已经不需要再往任何一个子问题递归了，就可以直接返回上一层，一般这种做法称为回溯法。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
//n皇后函数变量定义
const  int MAXN = 20;
int n;//输出index-n的全排列
int p[MAXN];
bool HashTable[MAXN]={false};
int my_count = 0;//记录合法的皇后排列个数
//n皇后问题递归函数
void n_queens(int index)
{
    //递归边界,到达递归边界都是合法序列
    if(index==n+1)
    {
        my_count++;
        return ;
    }
    //递归式
    for(int k=1;k<=n;k++)
    {
        if(!HashTable[k])//HashTable[k]==false->说明该元素还没有被用上
        {
            p[index]=k;//处理这一种情况
            HashTable[k] = true;//到这里说明假设1到index已经排好
            bool flag = true;
            for(int pre=1;pre<index;pre++)
            {
                if(abs(index-pre)==abs(p[index]-p[pre]))
                {
                    flag = false;
                    break;
                }
            }
            if(flag)
            {
                //递归进入函数再排index+1之后的部分
                n_queens(index+1);
            }
            //递归返回结束后循环还没有结束，继续处理下一循环的问题
            HashTable[k] = false;//已经处理完p[index]=k;这一种情况，还原状态
        }
    }
}
//主函数
int main(){
    n=8;
    n_queens(1);//index从1开始
    printf("%d",my_count);
    return 0;
}
  • 输出：
1
92

例题：反转字符串

  • 方法一：

  • 方法一代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//递归求字符串逆函数1
void rev_1(char* str)
{
    char temp;
    int len;
    temp = *str;
    len = strlen(str);
    *str = *(str+len-1);
    *(str+len-1)='\0';
    if(strlen(str+1)>=2)
    {
        rev_1(str+1);
    }
    *(str+len-1)=temp;
}
  • 方法二：

  • 方法二代码：
1
2
3
4
5
6
7
8
9
10
11
12
//递归求字符串逆函数2
void rev_2(char* str,int left,int right)
{
    char temp;
    temp = str[left];
    str[left] = str[right];
    str[right] = temp;
    if(left+1<right-1)
    {
        rev_2(str,left+1,right-1);
    }
}
  • 总代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int MAXN = 110;
char str[MAXN],rev_str[MAXN];
int n;
//递归求字符串逆函数1
void rev_1(char* str)
{
    char temp;
    int len;
    temp = *str;
    len = strlen(str);
    *str = *(str+len-1);
    *(str+len-1)='\0';
    if(strlen(str+1)>=2)
    {
        rev_1(str+1);
    }
    *(str+len-1)=temp;
}
//递归求字符串逆函数2
void rev_2(char* str,int left,int right)
{
    char temp;
    temp = str[left];
    str[left] = str[right];
    str[right] = temp;
    if(left+1<right-1)
    {
        rev_2(str,left+1,right-1);
    }
}
//主函数
int main(){
    scanf("%s",str);
    //rev_1(str);
    rev_2(str,0,strlen(str)-1);
    printf("%s", str);
    return 0;
}
  • 总结：上述介绍的两种方法可以多深入体会。

例题：上楼

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
//递归判断上楼梯方式数
int F(int n)
{
    if(n<=1)
        return 1;
    else
        return F(n-1)+F(n-2);//最后只有加一级或者两级，方案是固定的，所以只需要求出还需要一级到达的总方式数和还需要两级到达的总方式数即可
}
//主函数
int main(){
    int n;
    scanf("%d",&n);
    printf("%d",F(n));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：最后要到达最高级只有加一级或者两级，方案是固定的，所以只需要求出还需要一级到达的总方式数和还需要两级到达的总方式数即可。

例题：汉诺塔

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int my_count=0;
//汉诺塔问题
void hanoi(int n,char from,char to,char mid)
{
    if(n==1)
    {
        printf("%c->%c\n",from,to);
    }
    else
    {
        hanoi(n-1,from,mid,to);//要想移动n级汉诺塔需要先移动n-1级汉诺塔到另一边
        printf("%c->%c\n",from,to);//把最后最大的一块移动到目的位置
        hanoi(n-1,mid,to,from);//最后把剩下n-1级的汉诺塔移动到目标位置
    }
}
//主函数
int main(){
    int n;
    scanf("%d",&n);
    printf("%d\n",(int)pow(2,n)-1);
    hanoi(n,'A','C','B');
    return 0;
}
  • 总结：要想移动n级汉诺塔需要先移动n-1级汉诺塔到另一边，然后把最后最大的一块移动到目的位置，最后把剩下n-1级的汉诺塔移动到目标位置，从而形成递归。

例题：棋盘覆盖问题

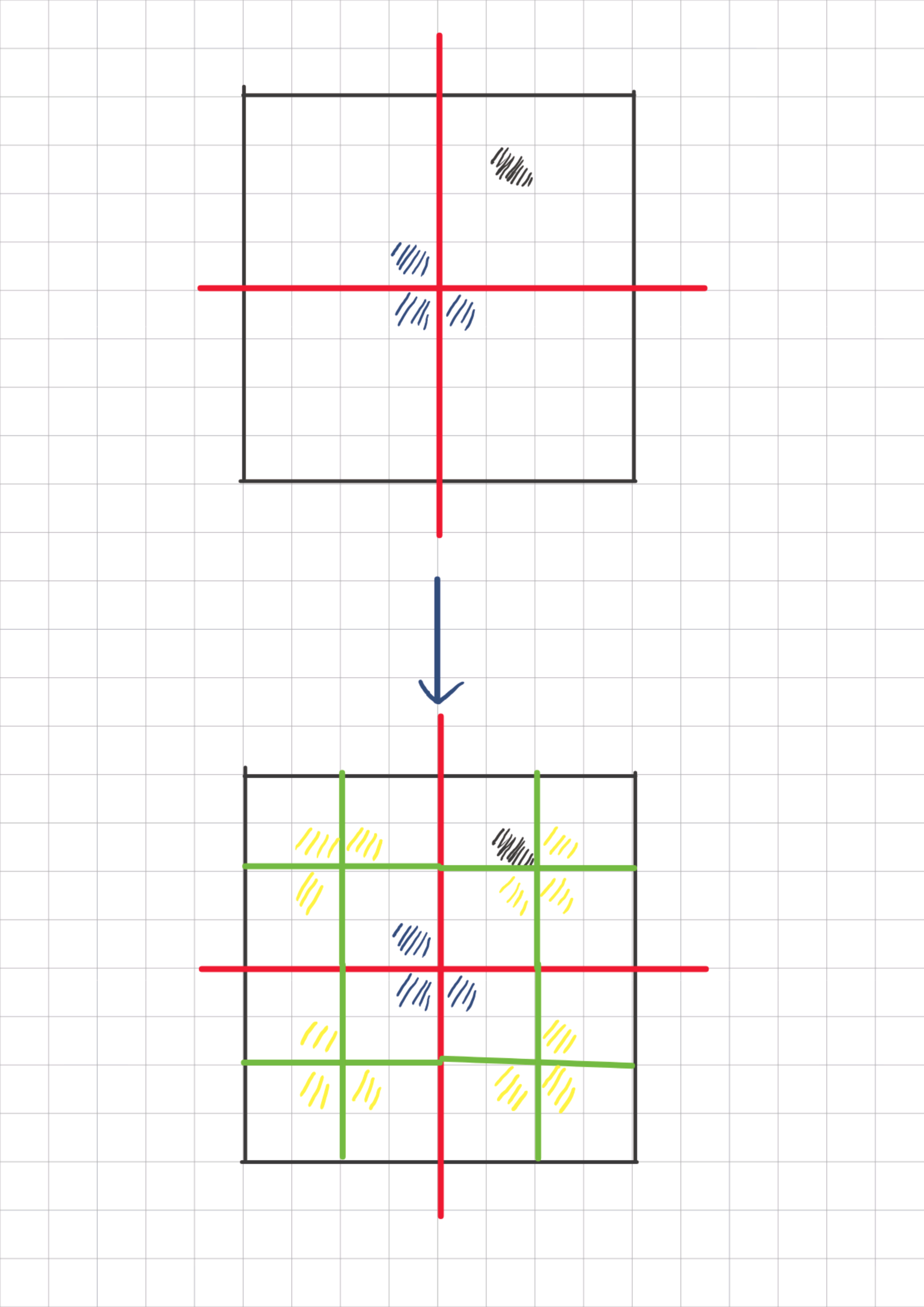
  • 说明：这道题目是一道典型的二维分治问题。
  • 思路：要想采用分治的方法并且使用递归来进行求解，就需要划分成相同方案的子问题，划分的思路如下：

  • 以此类推，在划分到只剩下2×2大小的方块后就很容易地采用骨牌进行填充。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int MAXN = 256*256;
int my_index = 0;
//建立坐标结构体
struct point
{
    int x , y;
    //原始构造函数，不需要初始化变量
    point(){}
    //传参构造函数
    point(int _x,int _y)
    {
        x=_x;
        y=_y;
    }
};
//定义存储的点数组
point arr[MAXN];
//递归获取棋盘覆盖函数
/*
x,y是左下角方格坐标，代表原点
cx,cy是黑点坐标
size是传入此函数时整体方格的大小
*/
void chees_cover(int x,int y,int cx,int cy,int size)
{
    int h;
    if(size == 1)
        return;
    h = size/2;
    //黑色方格在左上角
    if(cy>=y+h&&cx<x+h)//假如黑色方块在左上角
    {
        arr[my_index++]=point(x+h,y+h-1);//从黑色方块在左上角
        //确认骨牌的原点在右下角
        //以下的三个if语句同理
        chees_cover(x,y+h,cx,cy,h);
    }
    else
    {
        chees_cover(x,y+h, x+h-1,y+h,h);//
    }
    //黑色方格在右上角
    if(cy>=y+h&&cx>=x+h)
    {
        arr[my_index++]=point(x+h-1,y+h-1);
        chees_cover(x+h,y+h,cx,cy,h);
    }
    else
    {
        chees_cover(x+h,y+h,x+h,y+h,h);
    }
    //黑色方格在左下角
    if(cy<y+h&&cx<x+h)
    {
        arr[my_index++]=point(x+h,y+h);
        chees_cover(x,y,cx,cy,h);
    }
    else
    {
        chees_cover(x,y,x+h-1,y+h-1,h);
    }
    //黑色方格在右下角
    if(cy<y+h&&cx>=x+h)
    {
        arr[my_index++]=point(x+h-1,y+h);
        chees_cover(x+h,y,cx,cy,h);
    }
    else
    {
        chees_cover(x+h,y,x+h,y+h-1,h);
    }
}
//定义排序比较函数
int cmd(point px,point py)
{
    if(px.x==py.x)
    {
        return px.y < py.y;
    }
    else
    {
        return px.x < py.x;
    }
}
//主函数
int main(){
    int k,cx,cy,size;
    scanf("%d%d%d",&k,&cx,&cy);
    size = (int)pow(2,k);
    chees_cover(1,1,cx,cy,size);
    sort(arr,arr+my_index,cmd);
    for(int i=0;i<my_index;i++)
    {
        printf("%d %d\n",arr[i].x,arr[i].y);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

例题：谢尔宾斯基地毯

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int MAXN = 3*3*3*3*3*3*3;
char arr[MAXN][MAXN];
//定义谢尔宾斯基地毯递归函数
void cover(int n,int x,int y)
{
    int unit = (int)pow(3.0,n-2);
    if(n==1)
    {
        arr[x][y]=' ';
    }
    else
    {
        cover(n-1,x,y);
        cover(n-1,x,y+unit);
        cover(n-1,x,y+2*unit);
        cover(n-1,x+unit,y);
        for(int i=x+unit;i<x+2*unit;i++)
        {
            for(int j=y+unit;j<y+2*unit;j++)
            {
                arr[i][j]='X';
            }
        }
        cover(n-1,x+unit,y+2*unit);
        cover(n-1,x+2*unit,y);
        cover(n-1,x+2*unit,y+unit);
        cover(n-1,x+2*unit,y+2*unit);
    }
}
//主函数
int main(){
    int n,my_unit;
    scanf("%d",&n);
    my_unit = pow(3.0,n-1);
    for(int i=0;i<my_unit+2;i++)
    {
        for(int j=0;j<my_unit+2;j++)
        {
            if(i==0||i==my_unit+1||j==0||j==my_unit+1)
            {
                arr[i][j]='+';
            }
            else
                arr[i][j]=' ';
        }
    }
    cover(n,1,1);
    //printf("%d %d",n,my_unit);
    for(int i=0;i<my_unit+2;i++)
    {
        for(int j=0;j<my_unit+2;j++)
        {
            printf("%c",arr[i][j]);
        }
        printf("\n");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这种题目主要找准递归的起始位置，根据起始位置即可输出完整图形。

例题：有限制的选数II

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
using namespace std;
const int MAX = 15;
int n,k,ans=0;
int num[MAX];
//递归函数求解有限制的选数
void F(int index,int sum)
{
    //递归边界
    if(index==n)
    {
        if(sum==k)
            ans++;
        return;
    }
    //递归式
    for(int i=0;i<=(k-sum)/num[index];i++)//在循环中加上了本身的数据
    {
        F(index+1,sum+i*num[index]);//根据加上了本身的数据再继续往后递归
    }
}
//主函数
int main(){
    scanf("%d %d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num[i]);
    }
    F(0,0);
    printf("%d",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目的巧妙之处在于设计了在循环中加上了本身的数据，随后根据加上了本身的数据再继续往后递归。

例题：有限制的选数III

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
using namespace std;
const int MAX = 15;
const int MAXN = 150;
int n,k,ans=0,m;
int num[MAX],p[MAX];
int hashTable[MAXN] = {0};
//递归函数求解有限制的选数
void F(int index,int sum)
{
    //递归边界
    if(index==m)
    {
        if(sum==k)
            ans++;
        return;
    }
    //递归式
    for(int i=0;i<=min((k-sum)/p[index],hashTable[p[index]]);i++)//去除重复数据
    {
        F(index+1,sum+i*p[index]);
    }
}
//主函数
int main(){
    scanf("%d %d",&n,&k);
    //去除重复数据输入并且写入重复的数量到哈希表中
    m=n;
    int t[MAX];
    for(int i=0;i<n;i++)
    {
        scanf("%d",&t[i]);
        hashTable[t[i]]++;
        if(i>0&&t[i]==t[i-1])
        {
            m--;
        }
    }
    int l=0;
    for(int i=0;i<MAXN;i++)
    {
        if(hashTable[i]!=0)
        {
            p[l]=i;
            l++;
        }
    }
    // printf("%d\n",m);
    // for(int i=0;i<m;i++)
    // {
    //     printf("%d ",p[i]);
    // }
    F(0,0);
    printf("%d",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目的与上一道题目思路类似，巧妙之处同样在于设计了在循环中加上了本身的数据，随后根据加上了本身的数据再继续往后递归，不同点在于所能加上自身的数据从小于等于 k 变成了小于等于 k 和输入的数据本身的数量。

例题：背包问题

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
using namespace std;
const int MAX = 15;
const int MAXN = 10000110;
int n,k;
int num[MAX],value[MAXN];
int max_value = -1;
//递归函数求解有限制的选数
void F(int index,int sum,int temp_value)
{
    //递归边界
    if(index==n)
    {
        max_value = max(max_value,temp_value);
        //printf("%d %d\n",sum,max_value);
        return;
    }
    //递归式
    if(sum+num[index]<=k)//在进入增加总容量的递归前判断是否超过了背包容量，不一定能够正好达到背包最大容量
    {
        F(index+1,sum+num[index],temp_value+value[index]);
    }
    F(index+1,sum,temp_value);
}
//主函数
int main(){
    scanf("%d %d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num[i]);
    }
    for(int i=0;i<n;i++)
    {
        scanf("%d",&value[i]);
    }
    F(0,0,0);
    printf("%d",max_value);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目与上面的有限制的选数题目思路基本类似，主要不同点在于提供的数据不一定能够达到背包的最大容量，因此需要在进入增加总容量的递归前判断是否超过了背包容量。

例题：生成括号对

  • 思路：
  • n 个括号对，也就是说一共 2 n 个字符，我们可以枚举 n 个'('分别放在什么位置，剩下的自然就是')'了。看起来很有道理，但是有一个问题，就是这个思路并没有办法通过循环直接实现。这其实已经进化成了一个搜索问题了，我们要搜索所有可以摆放括号的可能性。
  • 对于搜索问题而言，这已经很简单了，我们搜索的空间是明确的，2 n 个位置，搜索的内容，对于每个位置我们可以摆放'('也可以摆放')'。
  • 我们来思考一个问题：什么情况会出现右括号 ')' 遇不到左括号 '(' 呢？只有一种情况，就是当前出现右括号的个数超过了左括号，也就是说我们遍历一下字符串，如果中途出现右括号数量超过左括号的情况，那么就说明这个字符串是非法的。
  • 看起来没毛病对吧，但是有问题，我们为什么不在枚举的时候就判断呢，如果左括号放入的数量已经等于右括号了，那么就不往里放置右括号，这样不就可以保证搜索到的一定是合法的字符串吗？
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
#include <set>
using namespace std;
//变量
int n;
set<string> st;
//递归函数生成括号对
void F(int pos,int left,int right,string cur_str)
{
    //pos:当前字符串长度
    //left:左括号数量
    //right:右括号数量
    //cur_str:当前字符串
    if(pos==2*n)
    {
        st.insert(cur_str);
    }
    if(left<n)
    {
        F(pos+1,left+1,right,cur_str+'(');
    }
    if(right<n&&right<left)
    {
        F(pos+1,left,right+1,cur_str+')');
    }
}
//主函数
int main(){
    scanf("%d",&n);
    F(0,0,0,"");
    for(set<string>::iterator it = st.begin();it!=st.end();it++)
    {
        cout << *it << endl;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：在 right < n 后面加入了一个 right < left 这个条件。看似只有一个条件，但是这个条件起到的作用至关重要。整个算法的效率有了质的提升，实际上这也是效率最高的算法。

例题：加号之和

  • 思路：以分解 361 为例：

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <vector>
#include <set>
using namespace std;
//变量
const int MAXN = 9;//字符串的最大长度
char data[MAXN];//存储数字
int n;
//函数
//head:开始字符的下标
//tail:结尾字符的下一个位置
int get_num(int head,int tail){
    int sum=0;
    for(int i=head;i<tail;i++){
        sum=sum*10+data[i]-'0';
    }
    return sum;
}
int sum_num(int head,int tail,int len){
    if(head+1==tail){
        return get_num(head,tail);
    }else{
        //printf("head=%d tail=%d len=%d##\n",head,tail,len);
        int sum=get_num(head,tail);
        //printf("sum=%d#\n",sum);
        for(int i=head+1;i<tail;i++){
            sum+=get_num(head,i)*pow(2,tail-i-1)+sum_num(i,tail,tail-i);
            //printf("get_num=%d#\n",get_num(head,i));
        }
        return sum;
    }
}
//主函数
int main (){ 
    scanf("%s",data);
    n=strlen(data);
    printf("%d",sum_num(0,n,n));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结（关键思想）：
  • 上述代码左边字符为什么使用 get_num(head,i)*pow(2,tail-i-1)，而不是继续进行递归，而右边继续进行递归，主要是因为：
  • 第一步：361 分解为 3 和 61 时，61 总共有 2^1=2 种划分，即单独的{61}以及{6,1}，和左边在一起求和时，即：3+61 以及 3+6+1，3 出现了 61 的划分次数 2，即所乘的 pow (2,tail-i-1) 。
  • 第二步：361分解为36,1时，因为在划分为3,61情况时，已经出现过3,6,1这种情况，为了避免重复出现3,6,1的情况，将36不在进行划分（因为其对应的所有划分情况在上一步已经出现过了），即直接使用 get_num(head,i)！

一种递归式的非零自然数全分解方法

  • 在开始讲之前，首先介绍一下这个方法针对的问题背景：一个非零自然数(1,2,3,……)既不重复也不遗漏地任意分解为非零自然数(如：3=1+1+1=1+2)，在本篇暂且称为非零自然数的全分解。
  • 在非零自然数的全分解中，总共有多少种分解方法，并列出所有分解方法，在本篇暂且称为非零自然数的全分解问题。
基本概念
  1. 分解末项
       + 一个分解中的最后一项称为分解末项。如“3=1+2”中分解末项为“2”，再如“3=1+1+1”中分解末项为“1”。
  2. 分解基数B
      + 分解基数，在数值上定义为分解末项的前一项，举个例子：“5=1+4”称为分解基数B=1的一个分解，“5=1+2+2”称为分解基数B=2的一个分解。
      + 我们也可以把“5=1+4”到“5=1+2+2”的过程理解为一个将分解末项“4”按分解基数B=2的分解。实际上这种理解更为重要，因为在本方法中，我们本质上也是针对分解末项的分解。
分解规则
  1. 关于分解基数
    • 分解基数单调不减。如：“7=2+5=2+1+4”为一个错误的分解过程，因为第一级分解基数为2，第二级分解基数为1，违反分解基数单调不减原则。所以，“7=2+5=2+2+3”才是一个正确的分解过程。
  2. 关于分解末项
    • 分解末项应不小于分解基数。如：“5=1+1+3”为一个正确的分解，“5=1+3+1”为一个错误的分解。

  • 根据前述的两条分解规则，对7的全分解过程如上图所示，可以看到总共有14种分解方法。实际上，7的全分解就是这14种分解方法。

例题：自然数分解之方案数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
//递归求解自然数分解方案数量函数
int func(int pre,int now)
{
    int temp=0;
    for(int i=1;2*i<=now;i++)
    {
        if(i>=pre)
        {
            temp+=func(i,now-i);
            temp++;
        }
    }
    return temp;
}
//主函数
int main(){
    int n,num;
    scanf("%d",&n);
    num = func(0,n);
    printf("%d",num);
    return 0;
}
  • 总结：
    • 递归边界是：当我们需要拆分的数为1时，表示无法拆分，因此返回0。
    • 总而言之，func(pre,now)所返回的整数表示该组合后续能够拆分的总数。

例题：自然数分解之最大积

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
//递归求解自然数分解之最大积
int func(int pre,int now)
{
    int my_max=-1;
    for(int i=1;2*i<=now;i++)
    {
        if(i>=pre)
        {
            my_max=max(my_max,max(i*(now-i),func(i,now-i)));
        }
    }
    return max(my_max,pre*my_max);
}
//主函数
int main(){
    int n,num;
    scanf("%d",&n);
    num = func(0,n);
    printf("%d",num);
    return 0;
}
  • 总结：这题与自然数分解之方案数较为相似，只需要把递归函数 temp 的计数改为计算乘积最大值即可。

动态规划

例题：数塔

  • 思路：数塔问题是经典的动态规划问题，通过归纳可以得到一个信息：

    • 如果要求出dp[i][j],那么一定要求出其两个子问题：
    • 从位置(i+1,j)到达最底层的最大和dp[i+1][j];
    • 从位置(i+1,j+1)到达最底层的最大和dp[i+1][j+1];
    • 即进行了一次决策，走位置(i,j)的左下还是右下：
    • 式子如下：
    1
    dp[i][j]=max(dp(i+1,j),dp(i+1,j+1))+f[i][j];
    • 把dp[i][j]称为问题的状态，而把上面的式子称为状态转移方程。

  • 例题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int MAXN = 25;
int f[MAXN][MAXN],dp[MAXN][MAXN];
int n;
//数塔递归函数（动态规划）
int getMax(int i,int j)
{
    if(i==n)
    {
        return f[n][j];
    }
    else
    {
        dp[i][j]=max(getMax(i+1,j),getMax(i+1,j+1))+f[i][j];
        return dp[i][j];
    }
}
//主函数
int main(){
    scanf("%d",&n);
    for(int k=1;k<=n;k++)
    {
        for(int m=1;m<=k;m++)
        {
            scanf("%d",&f[k][m]);
        }
    }
    dp[1][1]= getMax(1,1);
    printf("%d",dp[1][1]);
    return 0;
}

贪心

简单贪心

  • 贪心法是求解一类最优化问题的方法，它总是考虑在当前状态下局部最优 (或较优)。
  • 显然，如果采取较优而非最优的策略 (最优策略可能不存在或不易想到)，得到的全局结果也无法是最优的。而要获得最优结果，则要求中间的每步策略都是最优的，因此严谨使用贪心法来求解最优化问题需要对采取的策略进行证明。
  • 证明的一般思路是使用反证法以及数学归纳法，即假设策略不能导致最优解，然后通过一系列推导来得到矛盾，以此证明策略是最优的，最后用数学归纳法保证全局最优。
  • 因为贪心的证明往往比贪心的实现本身更加困难，因此在某个可行的策略以及无法举出反例的情况下可以勇敢地实现。

例题：PAT B1020 月饼

  • 题意：
  • 现有月饼需求量为 D，已知 n 种月饼各自的库存量和总售价，问如何销售这些月饼，使得可以获得的收益最大，并求最大收益。
  • 思路：
  1. 这里采用“总是选择单价最高的月饼出售，可以获得最大的收入”的策略。
  • 因此，对每种月饼，都根据其库存量和总售价来计算出该种月饼的单价。
  • 之后，将所有月饼按单价从高到低排序。
  1. 从单价高的月饼开始枚举：
  • 如果该种月饼的库存量不足以填补所有需求量，则将该种月饼全部卖出，此时需求量减少该种月饼的库存量大小，收益值增加该种月饼的总售价大小。
  • 如果该种月饼库存量足够供应需求量，则只需要提高需求量大小的月饼，此时收益值增加当前需求量乘以该种月饼的单价，而需求量减为 0。
  • 最后即可得到收益值即为所求的最大收益值。
  • 策略正确性证明：
  • 假设有两种单价不同的月饼，其单价分别为 a 和 b (a<b)。如果当前需求量为 K，那么两种月饼的总收入分别为 aK 和 bK ，而 aK<bK 显然成立，因此需要出售单价更高的月饼。
  • 注意点：
  1. 月饼库存量和总售价可以是浮点数（题目中只说是正数，没说是正整数），需要用 double 型存储。对于总需求量 D 虽然题目说是正整数，但是为了后面计算方便，也需要定义为浮点型。
  2. 当月饼库存量高于需求量时，不能先令需求量为 0，然后再计算收益，这会导致该步收益为 0。
  3. 当月饼库存量高于需求量时，记得将循环中断，否则会出错。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//月饼结构体
struct Mooncake
{
    double num;//月饼库存量
    double total_price;//总售价
    double price;//单价
};
//比较函数
bool cmd(Mooncake a,Mooncake b)
{
    return a.price > b.price;
}
//主函数
int main()
{
    vector<Mooncake> vi;
    int n;
    double need;
    double num,total_price;
    scanf("%d %lf",&n,&need);
    for(int i=0;i<n;i++)
    {
        Mooncake m;
        scanf("%lf",&num);
        m.num=num;
        vi.push_back(m);
    }
    for(int i=0;i<n;i++)
    {
        scanf("%lf",&total_price);
        vi[i].total_price = total_price;
        vi[i].price = total_price/vi[i].num;//计算每个月饼的单价
    }
    //完成单价从高到低排序
    sort(vi.begin(),vi.end(),cmd);
    //定义计算值
    double now_need = need;
    double now_total_price = 0;//总收入
    for(int i=0;i<n;i++)
    {
        if(vi[i].num<=now_need)//如果需求量高于月饼库存量
        {
            now_need -= vi[i].num;//则第i种月饼需要全部卖出
            now_total_price += vi[i].total_price;
        }
        else//如果月饼库存量高于需求量
        {
            //那么只需要卖出剩余需求量的月饼
            now_total_price += now_need*vi[i].price;
            break;
        }
    }
    printf("%.2f\n",now_total_price);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

例题：PAT B1023 组个最小数

  • 思路：
  • 策略是：先从 1~9 中选择个数不为 0 的最小数输出，然后从 0~9 输出数字，每个数字输出次数为其剩余个数。
  • 以样例为例：最高位为个数不为 0 的最小的数 1，此后 1 的剩余个数减 1（由 2 变为 1）。接着按剩余次数（0 剩余两个，1 剩余一个，5 剩余三个，8 剩余一个）依次输出所有数。
  • 策略正确性证明：
  • 首先，由于所有数字必须参与组合，因此最后结果的位数是确定的。然后，由于最高位不能为 0，因此从 [1,9] 中选择最小的数输出（如果存在两个长度相同的数的最高位不同，那么一定是高位小的数更小）。
  • 最后，针对除最高位外的所有位，也是从高位到低位优先选择 [0,9] 还存在的最小数输出。
  • 注意点：
  • 由于第一位不能是 0，因此第一个数字必须从 1~9 中选择最小的存在的数字，且找到这样的数字之后要及时中断循环。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//变量定义
const int MAX = 10;
int hashtable[MAX];
//主函数
int main()
{
    for(int i=0;i<MAX;i++)
    {
        scanf("%d",&hashtable[i]);
    }
    //输出第一位
    for(int i=1;i<MAX;i++)
    {
        if(hashtable[i]!=0)
        {
            printf("%d",i);
            hashtable[i]--;
            break;
        }
    }
    //输出后面位数
    for(int i=0;i<MAX;i++)
    {
        if(hashtable[i]!=0)
        {
            for(int j=0;j<hashtable[i];j++)
            {
                printf("%d",i);
            }
            hashtable[i]=0;
        }
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

区间贪心

  • 通过上述例子，能够对贪心有一个大致了解。以下是一个稍微复杂一些的问题：
  • 区间不相交问题：
  • 给出 N 个开区间 (x, y)，从中选择尽可能多的开区间，使得这些开区间两两没有交集。
  • 例如对开区间 (1,3)、(2,4)、(3,5)、(6,7) 来说，可以选出最多三个区间 (1,3)、(3,5)、(6,7)，它们互相没有交集。
  • 首先考虑最简单的情况，如果开区间 I1I_1 被开区间 I2I_2 包含，如下图 4-5 a 所示，那么显然选择 I1I_1 是最好的选择，因为如果选择 I1I_1，那么就有更大的空间去容纳其它开区间。

  • 接下来把所有开区间按左端点 x 从大到小排列，如果去除掉区间包含的情况，那么一定有 y1>y2>...>yny_1>y_2>...>y_n 成立，如上图 4-5b 所示。
  • 现在考虑应当如何选取区间，通过观察会发现，I1I_1 右边有一段是一定不会和其他区间重叠的，如果把它去掉，那么 I1I_1 的左边剩余部分就会被 I2I_2 包含，由图 4-5a 的情况可知，应当选择 I1I_1。
  • 因此对这种情况，总是先选择左端点最大的区间。

例题：区间不相交问题

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//变量定义
struct Inteval
{
    int x,y;//开区间左右端点
};
//比较函数
bool cmp(Inteval a,Inteval b)
{
    if(a.x!=b.x)
        return a.x > b.x;//先按左端点从大到小排序
    else
        return a.y < b.y;//左端点相同时按右端点从小到大排序
}
//主函数
int main()
{
    int n;
    vector<Inteval> vi;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        Inteval in;
        scanf("%d %d",&in.x,&in.y);
        vi.push_back(in);
    }
    sort(vi.begin(),vi.end(),cmp);//把区间排序
    //ans记录不相交区间个数，lastX记录上一个被选中区间的左端点
    int ans = 1,lastX = vi[0].x;
    for(int i=1;i<n;i++)//关键：从一开始循环,因为第一个自身天然算进去了
    {
        if(vi[i].y <= lastX)//如果该区间右端点lastX左边
        {
            lastX = vi[i].x;
            ans++;
        }
    }
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：
  • 值得注意的是，总是先选择右端点最小的区间的策略也是可行的，可以模仿上面思路推导，并写出相应代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//变量定义
struct Inteval
{
    int x,y;//开区间左右端点
};
//比较函数
bool cmp(Inteval a,Inteval b)
{
    if(a.y!=b.y)
        return a.y < b.y;//先按右端点从小到大排序
    else
        return a.x > b.x;//右端点相同时按左端点从大到小排序
}
//主函数
int main()
{
    int n;
    vector<Inteval> vi;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        Inteval in;
        scanf("%d %d",&in.x,&in.y);
        vi.push_back(in);
    }
    sort(vi.begin(),vi.end(),cmp);//把区间排序
    //ans记录不相交区间个数，lastY记录上一个被选中区间的右端点
    int ans = 1,lastY = vi[0].y;
    for(int i=1;i<n;i++)//关键：从一开始循环,因为第一个自身天然算进去了
    {
        if(vi[i].x >= lastY)//如果该区间左端点lastY右边
        {
            lastY = vi[i].y;
            ans++;
        }
    }
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 与上述问题相类似的是区间选点问题：
  • 给出 N 个闭区间 [x, y]，求至少需要确定多少个点，才能使每个闭区间中都至少存在一个点。
  • 例如对于闭区间[1,4]、[2,6]、[5,7] 来说，需要两个点（例如 3、5）才能保证每个闭区间内都至少有一个点。
  • 事实上，这个问题和区间不相交的策略是一致的。
  • 首先，回到图 4-5 a，如果闭区间 I1I_1 被闭区间 I2I_2 包含，那么在 I1I_1 中取点可以保证这个点一定在 I2I_2 内。
  • 接着，把所有区间按左端点从大到小排序，去除掉区间包含的情况，就可以到图 4-5 b。
  • 显然，由于每个闭区间中都需要存在一个点，因此对左端点最大的区间 I1I_1 来说，取哪个点可以让它尽可能多地覆盖其他区间？
  • 很显然，只要取左端点即可，这样这个点就能覆盖到尽可能多的区间。
  • 因此区间选点问题代码只需要把区间不相交问题代码中的条件 vi[i].y <= lastX 改为 vi[i].y < lastX 即可！

例题：区间选点问题

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//变量定义
struct Inteval
{
    int x,y;//开区间左右端点
};
//比较函数
bool cmp(Inteval a,Inteval b)
{
    if(a.x!=b.x)
        return a.x > b.x;//先按左端点从大到小排序
    else
        return a.y < b.y;//左端点相同时按右端点从小到大排序
}
//主函数
int main()
{
    int n;
    vector<Inteval> vi;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        Inteval in;
        scanf("%d %d",&in.x,&in.y);
        vi.push_back(in);
    }
    sort(vi.begin(),vi.end(),cmp);//把区间排序
    //ans记录不相交区间个数，lastX记录上一个被选中区间的左端点
    int ans = 1,lastX = vi[0].x;
    for(int i=1;i<n;i++)//从一开始循环,因为第一个自身天然算进去了
    {
        if(vi[i].y < lastX)//关键：如果该区间右端点lastX左边
        {
            lastX = vi[i].x;
            ans++;
        }
    }
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总的来说，贪心是用来解决一类最优化问题，并希望由局部最优策略来推得全局最优结果的算法思想。
  • 贪心算法适用的问题一定满足最优子结构性质，即一个问题的最优解可以由它的子问题的最优解有效地构造出来。
  • 显然，不是所有问题都适合使用贪心法，但是这并不妨碍贪心算法成为一个简洁、实用、高效的算法。

贪心算法例题

例题：拼接最小数

  • 思路：
  • 给定 n 个可能含有前导 0 的数字串，将它们按任意顺序拼接，使生成的整数最小。
  • 这道题其实思路很简单，就是对输入的字符串进行排序，然后就是前导 0，和全部为 0 的情况的特例考虑一下。
  • 但其实事实上会有个小坑点在里面，就是排序不是简单的字符串a<b。
  • 因为会有这样的例子：
  • 47，470 和 470，如果要输出应该是 47047047 这样比 47470470 要小！
  • 因此排序应该是 a+b < b+a；
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//比较函数
bool cmp(string a,string b)
{
    return a+b < b+a;//注意:关键点
}
//主函数
int main()
{
    int n;
    scanf("%d",&n);
    vector<string> vi;
    string str;
    for(int i=0;i<n;i++)
    {
        cin >> str;
        vi.push_back(str);
    }
    //排序
    sort(vi.begin(),vi.end(),cmp);
    //输出答案
    string ans = "";
    for(int i=0;i<n;i++)
    {
        ans+=vi[i];
    }
    //去除前导0
    while(ans[0]=='0')
    {
        ans.erase(ans.begin());
    }
    if(ans.length()==0)
        printf("0");
    else
        cout << ans << endl;
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：在做贪心问题的时候注意看清题意并找出题目中和自己代码中的需要关注的细节，必要时可以举些例子来更清楚地理解。

二分

二分查找

  • 先来看猜数字的游戏。
  • 在这个游戏中，玩家 A 从一个范围中选择一个数（例如从 [1,1000] 中选择了 352），然后让玩家 B 猜这个数字。
  • 此时，如果玩家 B 猜的数字 x 小于 352，说明 x< 352 ≤ 1000，应当在 [x+1,1000] 中继续猜；
  • 如果玩家 B 猜的数字 x 大于 352，说明 1 ≤ 352 < x,应当在 [1, x-1] 中继续猜。
  • 显然，每次选择当前范围的中间数字去猜，就能尽可能快地逼近正确的数字，并最终将其猜出来。
  • 该游戏的背后是一个经典的问题：
  • 如何在一个严格递增序列 A 找出给定的数 x。
  • 最直接的办法是：线性扫描序列中的所有元素，如果当前元素恰好为 x，则表明查找成功；如果扫描完整个序列都没有发现给定的数 x，则表明查找失败，说明序列中不存在数 x。这种顺序查找的时间复杂度为 O(n)O(n) (其中 n 为序列元素个数)，如果查询的次数不多，则是很好的选择，但是如果有 10510^5 个数需要查询，将不太能承受。
  • 更好的办法是使用二分查找：二分查找是基于有序序列的查找算法（以下以严格递增序列为例），该算法一开始令 [left, right] 为整个序列的下标区间，然后每次测试当前 [left, right] 的中间位置 mid=(left+right)/2，判断 A[mid] 与欲查询的元素 x 的大小：
  1. 如果 A[mid]==x，说明查找成功，退出查询。


2. 如果 A[mid]>x，说明元素 x 在 mid 位置的左边，因此往左子区间 [left, mid-1] 继续查找。


3. 如果 A[mid]<x，说明元素 x 在 mid 位置的右边，因此往右子区间 [mid+1, right] 继续查找。

  • 二分查找的高效之处在于，每一步都可以去除当前区间的一半元素，因此时间复杂度是 O(logn)O(logn)，这是十分优秀的。
  • 为了更好地解释二分查找地流程，举一个例子来模拟二分查找地过程：
  • 现在需要从序列 A={3,7,8,11,15,21,33,52,66,88} 中查询数字 11 和 34 的位置，其中序列下标从 1 到 10。
  • 首先是 11 的查询过程，令 left=1、right=10，表示当前查询的下标范围：
  1. [left,right]=[1,10]，因此下标中点 mid=(left+right)/2=5。由于 A[mid]=A[5]=15，而 15>11，说明需要在 [left,mid-1] 继续查找，因此令 right=mid-1=4。


2. [left,right]=[1,4]，因此下标中点 mid=(left+right)/2=2。由于 A[mid]=A[2]=7，而 7<11，说明需要在 [mid+1,right] 继续查找，因此令 left=mid+1=3。


3. [left,right]=[3,4]，因此下标中点 mid=(left+right)/2=3。由于 A[mid]=A[3]=8，而 8<11，说明需要在 [mid+1,right] 继续查找，因此令 left=mid+1=4。


4. [left,right]=[4,4]，因此下标中点 mid=(left+right)/2=4。由于A[mid]=A[4]=11，而 11==11，说明找到了欲查询的数字，因此结束算法，返回下标 4。

  • 接下来是 34 的查询过程，同样令 left=1、right=10：
  1. [left,right]=[1,10]，因此下标中点 mid=(left+right)/2=5。由于 A[mid]=A[5]=15，而 15<34，说明需要在 [mid+1,right] 继续查找，因此令 left=mid+1=6。


2. [left,right]=[6,10]，因此下标中点 mid=(left+right)/2=8。由于 A[mid]=A[8]=52，而 52>34，说明需要在 [left,mid-1] 继续查找，因此令 right=mid-1=7。


3. [left,right]=[6,7]，因此下标中点 mid=(left+right)/2=6。由于 A[mid]=A[6]=21，而 21<34，说明需要在 [mid+1,right] 继续查找，因此令 left=mid+1=7。


4. [left,right]=[7,7]，因此下标中点 mid=(left+right)/2=7。由于 A[mid]=A[7]=33，而 33<34，说明需要在 [mid+1,right] 继续查找，因此令 left=mid+1=8。


5. [left,right]=[8,7]，由于 left>right，因此查找失败，说明序列不存在 34。

  • 需要注意的是，二分查找的过程与序列的下标从 0 开始还是从 1 开始无关，整个过程是相同的。
  • 根据上述基础，给出在严格递增序列中查找给定的数 x 的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//二分查找函数
//A[]为严格递增序列，left为二分下界，right为二分上界，x为欲查询数
//二分区间为左闭右闭[left,right]，传入初值为[0,n-1]
int binarySearch(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left <= right) //如果left>right就没办法形成闭区间
    {
        mid = (left+right)/2; //取中点
        if(A[mid]==x) 
            return mid;//找到x，返回下标
        else if(A[mid]>x)//中间数大于查询数
            right = mid -1;//往左子区间查找
        else
            left = mid + 1;//往右子区间查找
    }
    return -1;//查找失败，返回-1
}
//主函数
int main()
{
    const int n = 10;
    int A[n] = {1,3,4,6,7,8,10,11,12,15};
    int s,t;
    s=binarySearch(A,0,n-1,6);
    t=binarySearch(A,0,n-1,9);
    printf("%d %d\n",s,t);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
3 -1
  • 如果是递减序列，只需要把上述代码中 A[mid]>x 改为 A[mid]<x 即可。
  • 需要注意的是，如果二分上界超过 int 型数据类型范围的一半，那么当欲查询元素在序列较靠后位置时，语句 mid = (left+right)/2; 中的 left+right 超出 int 型数据类型范围而导致溢出，此时一般使用 mid = left+(right-left)/2; 这条等价语句作为代替以避免溢出。
  • 另外，二分法可以使用递归进行实现，但是在程序设计时更多采用的是非递归的写法。
  • 接下来探讨更进一步的问题：
  • 如果递增序列 A 中的元素可能重复，那么如何对给定的欲查询元素 x，求出序列中第一个大于等于 x 的元素位置 L 以及第一个大于 x 的元素的位置 R,这样元素 x 在序列中存在的区间就是左闭右开区间 [L,R)。
  • 例如对下标从 0 开始，有 5 个元素的序列 {1,3,3,3,6} 来说，如果要查询 3，则应当得到 L=1、R=4；
  • 如果要查询 5，则应当得到 L=R=4；
  • 如果要查询 6，则应当得到 L=4、R=5；
  • 如果要查询 8，则应当得到 L=R=5；
  • 显然，如果序列中没有 x，那么 L 和 R 也可以理解为假设序列中存在 x，则 x 应当在的位置。
  • 首先考虑第一个小问题：求序列中第一个大于等于 x 的元素位置。
  • 做法与之前的问题类似，假设当前区间为左闭右闭区间 [left,right]，那么可以根据 mid 位置处的元素与欲查询元素 x 的大小来判断应当往哪个子区间继续查找；
  1. 如果 A[mid]≥x，说明第一个大于等于 x 的元素位置一定在 mid 处或 mid 的左侧，应该往左子区间 [left,mid] 继续查询，即令 right=mid。


2. 如果 A[mid]<x，说明第一个大于等于 x 的元素位置一定在 mid 的右侧，应该往右子区间 [mid+1,right] 继续查询，即令 left=mid+1。

  • 由此可以写出对应函数的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//A[]为递增序列，x为欲查询数，函数返回第一个大于等于x的元素位置
//二分区间为左闭右闭[left,right]，传入初值为[0,n]
int lower_bound(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left<right)
    {
        mid = (left+right)/2;//取中点
        if(A[mid]>=x)//中间的数大于等于x
        {
            right = mid;//往左区间[left,mid]查找
        }
        else
        {
            left = mid + 1;//往右子区间[mid+1,right]查找
        }
    }
    return left;//返回L(夹出来)的位置
}
  • 上述代码有几个需要注意的地方：
  1. 循环条件为 left<right 而非之前的 left≤right，这是由问题本身决定的。
  • 在上一个问题中，需要当元素不存在时返回 -1，这样当 left>right 时 [left,right] 就不再是闭区间，可以以此作为元素不存在的判定原则，因此需要在 left≤right 满足时一直执行；
  • 但是如果想要返回第一个大于等于 x 的元素的位置，就不需要判断 x 本身是否存在，因为就算它不存在，返回的也是“假设它存在，它应该在的位置”，于是 left==right 时，[left,right] 刚好能夹出唯一的位置，就是需要的结果，因此只需要当 left<right 时让循环一直执行即可。
  1. 由于当 left==right 时 while 循环停止，因此最后的返回值既可以是 left，也可以是 right。
  2. 二分的初始区间应当能覆盖到所有可能返回的结果。

  • 首先，二分下界是 0 是显然的，但是二分上界是 n-1 还是 n 呢？

  • 考虑到欲查询元素有可能比序列中的所有元素都要大，此时应当返回 n（假设它存在，它应该在的位置），因此二分上界是 n，故二分的初始区间为 [left,right]=[0,n]。

  • 接下来考虑第二个小问题：求序列中第一个大于 x 的元素的位置。

  • 做法是类似的：

  • 假设当前区间 [left,right]，那么可以根据 mid 位置的元素与欲查询元素 x 的大小来判断应当往哪个子区间继续查找：

  1. 如果 A[mid]>x，说明第一个大于 x 的元素的位置一定在 mid 处或 mid 的左侧，应往左子区间 [left,mid] 继续查询。


2. 如果 A[mid]≤x，说明第一个大于 x 的元素的位置一定在 mid 的右侧，应往右子区间 [mid+1,right] 继续查询。

  • 于是可以写出寻找第一个大于 x 的函数代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//A[]为递增序列，x为欲查询数，函数返回第一个大于x的元素位置
//二分区间为左闭右闭[left,right]，传入初值为[0,n]
int upper_bound(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left<right)//对[left,right]来说，left==right意味着找到唯一位置
    {
        mid = (left+right)/2;//取中点
        if(A[mid]>x)//中间的数大于x
        {
            right = mid;//往左区间[left,mid]查找
        }
        else
        {
            left = mid + 1;//往右子区间[mid+1,right]查找
        }
    }
    return left;//返回夹出来的位置
}
  • 不难发现，和 lower_bound 函数的代码相比，upper_bound 函数只是把代码中的 A[mid]≥x 改成了 A[mid]>x，其他完全相同。
  • 实际上，lower_bound 函数和 upper_bound 函数都在解决这样一个问题：寻找有序序列中第一个满足某条件的元素的位置。
  • 这是一个非常重要且经典的问题，平时能碰到的大部分二分法问题都可以归结于这个问题。
  • 例如对 lower_bound 函数来说，它寻找的就是第一个满足条件“值大于等于 x”的元素的位置；
  • 而对 upper_bound 函数来说，它寻找的就是第一个满足条件“值大于 x”的元素的位置；
  • 因此，我们能够总结出此类问题的固定模板：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//解决“寻找有序序列第一个满足某条件的元素的位置”问题的固定模板
//A[]为递增序列，x为欲查询数
//二分区间为左闭右闭[left,right]，初值必须能覆盖解的所有可能取值
int solve(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left<right)//对[left,right]来说，left==right意味着找到唯一位置
    {
        mid = (left+right)/2;//取中点
        if(条件成立)//条件成立，第一个满足条件的元素的位置<=mid
        {
            right = mid;//往左区间[left,mid]查找
        }
        else//条件不成立，则第一个满足条件的元素的位置>mid
        {
            left = mid + 1;//往右子区间[mid+1,right]查找
        }
    }
    return left;//返回夹出来的位置
}
  • 显然，所谓的“某条件”在序列中一定是从左到右先不满足，然后满足的（否则把该条件取反即可）。
  • 另外，如果想要寻找最后一个满足 "条件C" 的元素的位置，则可以先求第一个满足 "条件!C" 的元素的位置，然后将该位置减 1 即可（后续小节中最长回文子串的二分解法用到了这一点）
  • 需要指出的是，虽然上面的模板使用了左闭右闭的二分区间来实现，但事实上使用左开右闭的写法也可以，并且与左闭右闭的写法等价。
  • 在这种做法下，二分区间是左开右闭区间 (left,right]，因此循环条件应当是 left+1<right，这样当退出循环时有 left+1==right 成立，使得 (left,right] 才是唯一位置。
  • 而由于变成了左开，left 的初值要比解的最小值小 1（例如对于下标从 0 开始的序列来说，left 和 right 的取值应为 -1 和 n），同时语句 left=mid+1 应当改为 left=mid（这一步十分关键，因为对于左边的 left 是开区间，取不到，可以仔细思考！），并且返回的应当是 right 而不是 left，同样是因为左边是开区间无法取到！
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//解决“寻找有序序列第一个满足某条件的元素的位置”问题的固定模板
//A[]为递增序列，x为欲查询数
//二分区间为左开右闭(left,right]，初值必须能覆盖解的所有可能取值
//left比最小取值小1
int solve(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left+1<right)//对(left,right]来说，left+1==right意味着找到唯一位置
    {
        mid = (left+right)/2;//取中点
        if(条件成立)//条件成立，第一个满足条件的元素的位置<=mid
        {
            right = mid;//往左区间(left,mid]查找
        }
        else//条件不成立，则第一个满足条件的元素的位置>mid
        {
            //这一步十分关键，因为对于左边的left是开区间，取不到
            left = mid;//往右子区间(mid,right]查找
        }
    }
    return right;//返回夹出来的位置
}
  • 上述模板和前面是等价的，只是在做法上稍有区别而已，尽量使用左闭右闭的模板，但最好能做到流畅推导两种写法。
  • 可以思考如何判断 lower_bound 函数和 upper_bound 函数的查询是否成功（注意：上界 n 的处理即可）。
  • 最后指出，在目的是查找“序列中是否存在满足某条件的元素”，那么使用本小节最开始的二分查找写法最为合适。
二分查找例题

例题：旋转数组、旋转数组II

  • 思路：仔细观察这两道题目所给数据的规律，可以发现旋转之后的顺序虽然整体不是升序或者降序排列的，但是在某个断点处的两边分别是按照升序或者降序排列的两段数据。以下面的数据为例：

  • 不难发现，只要当我们获取到断点的坐标，就能分别根据断点左右两边的有序数组来进行元素的二分查找。
  • 在此给出寻找断点部分的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//寻找断点
    while(A[0]>=A[n-1]&&left<right)//保证是选择后的数组且left<right
    {
        int mid=(left+right)/2;//取中点
        //left和right一定分布在断点的左右两侧
        //mid有可能在断点的左边也有可能在断点的右边
        //通过观察可以判断，A[mid]>A[left]则断点一定在右边
        //反之则一定在左边。
        if(A[mid]>A[left])
        {
            left=mid;
        }
        else
        {
            right=mid;
        }
    }
    int point=left;//存储断点
  • 关键点：通过上述代码不难发现， left 和 right 一定分布在断点的左右两侧，而 mid 有可能在断点的左边也有可能在断点的右边。
  • 通过观察可以判断 A[mid]>A[left] 则断点一定在右边，反之则一定在左边。
  • 循环判断条件 A[0]>=A[n-1] 的分析：题目所给的数据并不一定是按照升序或者降序排列的。例如令数据 [0,1,2] 在下标为 0 的位置上进行旋转，则旋转后的数组仍为 [0,1,2]，这个时候就不需要进行第一步断点的搜寻，而是可以直接按照传统的二分法进行求解。
  • 通过 A[0]>=A[n-1] 来判断数组是否旋转的原因：

  • 接下来是判断目标元素 x 在断点的左半边还是右半边，通过 x>A[0] 这一个条件即可：

  • 最后使用前面的 lower_bound() 函数来寻找目标元素 x 即可。
  • 完整代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX = 100010;
//A[]为递增序列，x为欲查询数，函数返回第一个大于等于x的元素位置
//二分区间为左闭右闭[left,right]，传入初值为[0,n]
int lower_bound(int A[],int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left<right)
    {
        mid = (left+right)/2;//取中点
        if(A[mid]>=x)//中间的数大于等于x
        {
            right = mid;//往左区间[left,mid]查找
        }
        else
        {
            left = mid + 1;//往右子区间[mid+1,right]查找
        }
    }
    return left;//返回L(夹出来)的位置
}
//解决函数
int solve(int A[],int left,int right,int x,int n)
{
    //寻找断点
    while(A[0]>=A[n-1]&&left<right)
    {
        int mid=(left+right)/2;//取中点
        //printf("mid=%d\n",mid);
        if(A[mid]>A[left])
        {
            left=mid;
        }
        else
        {
            right=mid;
        }
    }
    int point=left;//存储断点
    //return left;
    //printf("point=%d\n",left);
    //判断目标元素在断点的左半边还是右半边
    if(x==A[0])
        return 0;
    else if(point!=0&&x>A[point])
        return -1;
    else if(point==0)
    {
        int ans=lower_bound(A,0,n,x);
        if(A[ans]==x)
            return ans;
        else
            return -1;
    }
    else if(x>A[0])//在左边
    {
        int ans=lower_bound(A,0,point,x);
        if(A[ans]==x)
            return ans;
        else
            return -1;
    }
    else//否则在右边
    {
        int ans=lower_bound(A,point,n-1,x);
        if(A[ans]==x)
            return ans;
        else
            return -1;
    }
}
//主函数
int main()
{
    int A[MAX];
    int x;
    int n,num;
    int ans;
    scanf("%d %d",&n,&x);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num);
        A[i]=num;
    }
    ans = solve(A,0,n-1,x,n);
    printf("%d",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

例题：旋转数组的中位数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX = 100010;
//解决函数
double solve(double A[],int left,int right,int n)
{
    //寻找断点
    while(A[0]>=A[n-1]&&left<right)
    {
        int mid=(left+right)/2;
        //printf("left=%d,right=%d,mid=%d\n",left,right,mid);
        if(A[mid]>A[left])
        {
            left=mid;
        }
        else
        {
            right=mid;
        }
    }
    int point=left;//存储断点
    //printf("%d\n",point);
    //关键在于寻找中位数的位置与断点之间的关系
    if(point==0)
    {
        if(n%2==1)//奇数
        {
            return A[n/2];
        }
        else
        {
            return (A[n/2-1]+A[n/2])/2;
        }
    }
    else
    {
        int ans;
        if(n%2==1)//奇数
        {
            int index1;
            if(point+n/2+1>n-1)
            {
                index1=point-n/2;
            }
            else
                index1=point+n/2+1;
            return A[index1];
        }
        else
        {
            int index1,index2;
            if(point+n/2+1>n-1)
            {
                index1=point-n/2+1;
            }
            else
                index1=point+n/2+1;
            if(point+n/2>n-1)
            {
                index2=point-n/2;
            }
            else
                index2=point+n/2;
            return (A[index1]+A[index2])/2;
        }
    }
}
//主函数
int main()
{
    double A[MAX];
    int x;
    int n;
    double ans;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%lf",&A[i]);
    }
    ans = solve(A,0,n-1,n);
    printf("%.1f",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目的关键点在于寻找中位数的位置与断点之间的关系！

例题：双序列中位数、寻找两个有序数组的中位数

  • 方法一：
  • 类似于暴力解法，使用二分查找法中的 upper_bound() 函数寻找合适的位置合并两个数组，最后得到中位数结果，在 leetcode 上执行用时 32ms。

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
//A[]为递增序列，x为欲查询数，函数返回第一个大于x的元素位置
//二分区间为左闭右闭[left,right]，传入初值为[0,n]
int upper_bound(vector<double>& A,int left,int right,int x)
{
    int mid; //mid为left和right的中点
    while(left<right)//对[left,right]来说,left==right意味着找到唯一位置
    {
        mid = (left+right)/2;//取中点
        if(A[mid]>x)//中间的数大于x
        {
            right = mid;//往左区间[left,mid]查找
        }
        else
        {
            left = mid + 1;//往右子区间[mid+1,right]查找
        }
    }
    return left;//返回夹出来的位置
}
//主函数
int main()
{
    vector<double> vi;
    int m,n;
    double num;
    int index;
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%lf",&num);
        vi.push_back(num);
    }
    for(int i=0;i<m;i++)
    {
        scanf("%lf",&num);
        index = upper_bound(vi,0,vi.size(),num);
        vector<double>::iterator it = vi.begin();
        vi.insert(it+index,num);
    }
    if(vi.size()%2==1)//奇数
    {
        printf("%.1f\n",vi[vi.size()/2]);
    }
    else
    {
        printf("%.1f\n",(vi[vi.size()/2-1]+vi[vi.size()/2])/2);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 方法二：划分数组
  • 思路：
  • 中位数定义：在只有一个有序数组的时候，中位数把数组分割成两个部分。
  • 根据定义，需要分数组长度为奇数和偶数讨论：
  • 数组长度为偶数时，中位数有两个，其中一个是左边数组的最大值，另一个是右边数组的最小值。如下图所示：

  • 数组长度为奇数时，中位数有一个，不妨把中位数分到左边数组。如下图所示：

  • 在两个有序数组的时候，仍然可以把两个数组分割成两部分：

  • 我们可以使用一条分割线把两个数组分割成两部分，其中有以下两个条件：
  1. 红色分割线左边和右边的元素个数相等，或者左边元素的个数比右边元素个数多 1 个；
  2. 红色分割线左边的所有元素的数值小于等于红色分割线右边的所有元素的数值；
  • 那么中位数就一定只与红色分割线两侧的元素有关，确定这条红色分割线采用二分查找法！
  • 第一个条件：
  • 例如奇数情况，分割线左边 5 个元素，右边 4 个元素：

  • 当两个数组的元素个数之和为奇数的时候，有 sizeleft=sizeright+1size_{left}=size_{right}+1
  • 例如偶数情况，分割线左边 5 个元素，右边 5 个元素：

  • 当两个数组的元素个数之和为偶数的时候，有 sizeleft=sizerightsize_{left}=size_{right}
  • 假设数组 1 的长度为 m，假设数组 2 的长度为 n；
  • 当 m+n 为偶数的时候，sizeleft=m+n2size_{left}=\frac{m+n}{2}，由于整数除法是下取整，因此也可以有如下关系 sizeleft=m+n2=m+n+12size_{left}=\frac{m+n}{2}=\frac{m+n+1}{2}；
  • 当 m+n 为奇数的时候，sizeleft=m+n+12size_{left}=\frac{m+n+1}{2}；
  • 因此，可以把上述两种方法合并，有 sizeleft=m+n+12size_{left}=\frac{m+n+1}{2}；
  • 上述结论的好处是，不用分奇偶数进行讨论，只需要确定其中一个数组的分割线位置，另一个数组的分割线位置就可以通过公式计算出来。
  • 第二个条件：
  • 红线左边的所有元素数值要小于等于红线右边的所有元素数值。由于两个数组都是有序数组，在同一个数组内，分割线一定满足左边的所有元素小于等于右边的所有元素；在不同的数组之间，应该保证交叉小于等于的关系，如下图所示：

  • 只要不符合交叉小于等于的关系，就需要适当调整分割线的位置。
  • 四种特殊的情况：


  • 从上面的分析中，不难发现需要做的是：

在 [0,m] 中找到 i，使得：
nums1[i-1]<=nums2[j] 且 nums2[j-1]<=nums1[i]，其中 j=m+n+12−ij=\frac{m+n+1}{2}-i

  • 可以证明上述条件等价于：

在 [0,m] 中找到最大的 i，使得：
nums1[i-1]<=nums2[j]，其中 j=m+n+12−ij=\frac{m+n+1}{2}-i

  • 这是因为：
  • 当 i 从 0~m 递增时，nums1[i-1] 递增，nums2[j] 递减，所以一定存在一个最大的 i 满足 nums1[i-1]<=nums2[j]；
  • 如果 i 是最大的, 那么说明 i+1 不满足。
  • 将 i+1 代入可以得到 nums1[i]>nums2[j-1]，也就是 nums2[j-1]<nums1[i]，就和进行等价变换前 i 的性质一致了（甚至还要更强了）。
  • 因此我们可以对 i 在 [0,m] 的区间上进行二分搜索，找到最大满足 nums1[i-1]<=nums2[j] 的 i 的值，就得到了划分的方法。
  • 此时，划分前一部分元素中的最大值，以及划分后一部分元素中的最小值，才可能作为就是这两个数组的中位数。
  • 该算法执行效率为 O(log(min(m,n))O(log(min(m,n))，达到最优效率：

  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
using namespace std;
//解决函数
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        //为了使得分割线的两侧在第二个数组的两侧都有元素，做此处处理，避免数组下标越界
        if(nums1.size()>nums2.size())
            return findMedianSortedArrays(nums2,nums1);
        //获取数组长度
        int m=nums1.size();
        int n=nums2.size();
        //分割线左边元素个数需要满足(m+n+1)/2
        int totalLeft = (m + n + 1)/2;
        //在nums1的区间[0,m]内寻找恰当的分割线
        //要使得能够直接找到中位数，需要满足以下条件
        //nums1[i-1]<=nums2[j]&&nums2[j-1]<=nums1[i];
        int left = 0;
        int right = m;
        while(left<right)
        {
            //i,j需要满足i+j= totalLeft = (m + n + 1)/2;
            //两个数组的分割线左边元素要与右边元素大致相等
            int i = left + (right - left + 1)/2;//上取整，避免进入死循环
            int j =  totalLeft - i;
            if(nums1[i-1]>nums2[j])//分割线在第一个数组太靠右了
                //下一轮搜索区间[left,i-1]
                right = i-1;
            else
                //下一轮搜索区间[i,right]
                //当表达式是left=i时，取中位数要上取整，避免进入死循环
                left = i;
        }
        //得到分割线
        int i = left;
        int j =  totalLeft - i;
        //注意下面需要排除没有意义的情况
        int nums1LeftMax = (i==0 ? INT_MIN : nums1[i-1]);
        int nums1RightMin = (i==m ? INT_MAX : nums1[i]);
        int nums2LeftMax = (j==0 ? INT_MIN : nums2[j-1]);
        int nums2RightMin = (j==n ? INT_MAX : nums2[j]);
        //分m+n奇偶来输出中位数
        if((m+n)%2==1)//奇数
            return (double) max(nums1LeftMax,nums2LeftMax);//返回分割线左边元素的最大值
        else
            //返回分割线左边元素的最大值和右边元素最小值的平均值
            return (double)(((double) max(nums1LeftMax,nums2LeftMax)+(double) min(nums1RightMin,nums2RightMin))/2);
}
//主函数
int main()
{
    int m,n,num;
    vector<int> nums1;
    vector<int> nums2;
    scanf("%d %d",&m,&n);
    for(int i=0;i<m;i++)
    {
        scanf("%d",&num);
        nums1.push_back(num);
    }
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num);
        nums2.push_back(num);
    }
    double ans;
    ans = findMedianSortedArrays(nums1,nums2);
    printf("%.1f",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：注意一下当表达式是 left=i 时，取中位数要上取整 int mid = left + (right - left + 1)/2;，避免进入死循环！

二分法拓展

  • 上面是应用于整数情况的二分查询问题，下面介绍二分法的其他应用：如何计算 2\sqrt{2} 的近似值。
  • 对 f(x)=x2f(x)=x^2 来说，在 x∈[1,2]x\in[1,2] 范围内，f(x)f(x) 是随着 xx 增大而增大的，这就给二分法创造了条件，即可以采用如下策略逼近 2\sqrt{2} 的值。(注意：由于 2\sqrt{2} 是无理数，因此只能获得它的近似值，这里不妨以精确到 10−510^{-5} 为例)
  • 令浮点型 left 和 right 的初值分别为 1 和 2，根据 left 和 right 的中点 mid 处 f(x)f(x) 的值与 2 的大小来选择子区间进行逼近；
  1. 如果 f(mid)>2f(mid)>2，说明 mid>2mid>\sqrt{2},应当在 [left,mid] 的范围内继续逼近，故令 right==mid。


2. 如果 f(mid)<2f(mid)<2，说明 mid<2mid<\sqrt{2},应当在 [mid,right] 的范围内继续逼近，故令 left==mid。

  • 上述两个步骤当 right−left<10−5right-left<10^{-5} 时结束。
  • 显然当 left 与 right 的距离小于 10−510^{-5} 时已经满足精度要求，mid 即为所求的近似值。
  • 通过上述思想可以得到如下代码，其中 eps 为精度，1e-5 即为 10−510^{-5}：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//常数定义
const double eps = 1e-5;//精度
//函数
double f(double x)
{
    return x*x;
}
//二分法求解函数
double calSqrt()
{
    double left = 1;
    double right = 2;//[left,right] = [1,2]
    double mid;
    while(right - left > eps)
    {
        mid = (left+right)/2;//取left与right的中点
        if(f(mid)>2) //mid > sqrt(2)
        {
            right = mid;//往左子区间[left,mid]继续逼近
        }
        else//mid < sqrt(2)
        {
            left = mid;//往右子区间[mid,right]继续逼近
        }
    }
    return mid;//返回近似值
}
  • 事实上，计算 2\sqrt{2} 的近似值的问题其实是这样一个问题的特例：
  • 给定一个定义在 [L,R] 上的单调函数 f(x)f(x)，求方程 f(x)=0f(x)=0 的根。
  • 同样，假设精度要求为 eps=10−5eps=10^{-5}，函数 f(x)f(x) 在 [L,R] 上递增，并令 left 与 right 的初值分别为 L 和 R，然后就可以根据 left 与 right 的中点 mid 的函数值 f(mid)f(mid) 与 0 的大小关系来判断应该往哪个子区间继续逼近 f(x)=0f(x)=0 的根
  1. 如果 f(mid)>0f(mid)>0，说明 f(x)=0f(x)=0 的根在 mid 左侧, 应当在 [left,mid] 的范围内继续逼近，故令 right==mid。


2. 如果 f(mid)<0f(mid)<0，说明 f(x)=0f(x)=0 的根在 mid 右侧, 应当在 [mid,right] 的范围内继续逼近，故令 left==mid。

  • 上述的步骤当 right−left<10−5right-left<10^{-5} 时达到精度要求时结束算法，返回当前的 mid 值即为 f(x)=0f(x)=0 的根。
  • 由此写出对应的二分法代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//常数定义
const double eps = 1e-5;//精度
//函数
double f(double x)
{
    return ......;//根据所求函数表达式更改
}
//二分法求解函数
double solve(double L,double R)
{
    double left = L;
    double right = R;//[left,right] = [L,R]
    double mid;
    while(right - left > eps)
    {
        mid = (left+right)/2;//取left与right的中点
        if(f(mid)>0) //mid > sqrt(2)
        {
            right = mid;//往左子区间[left,mid]继续逼近
        }
        else//mid < sqrt(2)
        {
            left = mid;//往右子区间[mid,right]继续逼近
        }
    }
    return mid;//返回近似值
}
  • 显然，计算 2\sqrt{2} 的近似值等价于求 f(x)=x2−2=0f(x)=x^2-2=0 在 [1,2] 范围内的根。
  • 另外，如果 f(x)f(x) 递减，只需要把代码中的 f(mid)>0f(mid)>0 改为 f(mid)<0f(mid)<0 即可。
  • 接下看一个装水问题：
  • 有一个侧面看去是半圆的储水装置，该半圆的半径为 R，要求往里面装入高度为 h 的水，使其在侧面看去的面积与半圆面积的比例恰好为 r，如图 4-6 所示。现在给定 R 和 r，求高度 h。

  • 在这个问题中，需要寻找水面高度 h 与面积比例 r 之间的关系。
  • 显然的是，随着水面升高，面积比例 r 一定是增大的。
  • 如果计算得到的 r 比给定数值要大，说明高度过高，范围应缩减至较低的一半；
  • 如果计算得到的 r 比给定数值要小，说明高度过低，范围应缩减至较高的一半；
  • 根据上述关系推导出函数表达式 r=f(h)r=f(h)，可以参考如下例题：

例题：装水问题

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
//常数定义
const double eps = 1e-5;//精度
const double PI = acos(-1.0);
//函数表达式
double f(double R,double h)
{
    double alpha = 2*acos((R-h)/R);//夹角
    double L = 2*sqrt(R*R-(R-h)*(R-h));//三角形底边长
    double H = R-h;//三角形的高
    double S1 = alpha*R*R/2-L*H/2;
    double S2 = PI*R*R/2;
    return S1/S2;
}
//二分法求解函数
double solve(double R,double r)
{
    double left = 0;
    double right = R;//[left,right] = [0,R]
    double mid;
    while(right - left > eps)
    {
        mid = (left+right)/2;//取left与right的中点
        //printf("%f %f %f\n",mid,f(R,mid),r);
        if(f(R,mid)>r) 
        {
            right = mid;//往左子区间[left,mid]继续逼近
        }
        else
        {
            left = mid;//往右子区间[mid,right]继续逼近
        }
    }
    return mid;//返回近似值
}
//主函数
int main()
{
    double R,r;
    scanf("%lf%lf",&R,&r);
    printf("%.2f\n",solve(R,r));
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 接下看一个木棒切割问题：
  • 给出 N 根木棒，长度均已知，现在希望通过切割它们来得到至少 K 段长度相等的木棒（长度必须是整数），问这些长度相等的木棒最长能有多长？
  • 例如对三根长度分别为 10、24、15 的木棒来说，假设 K=7，即需要至少 7 段长度相等的木棒，那么可以得到的最大长度为 6。
  • 在这种情况下，第一根木棒可以提供 10/6=1 段；
  • 第二根木棒可以提供 24/6=4 段；
  • 第三根木棒可以提供 15/6=2 段；
  • 因此达到了 7 段的要求。
  • 对于这个问题来说，可以注意到一个结论：
  • 如果长度相等的木棒长度 L 越长，那么可以得到的木棒段数 k 越少。
  • 从这个角度出发便可以想到本题的算法，即二分答案（最大长度 L），根据对当前长度 L 来说能得到的木棒段数 k 与 K 的大小关系进行二分。
  • 由于这个问题可以写成求解最后一个满足条件 "k≥K" 的长度 L，因此不妨转换为求解第一个满足条件 "k<K" 的长度 L，然后减 1 即可。

例题：木棒切割问题

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
//变量定义
vector<int> vi;
//比较函数
bool cmp(int a,int b)
{
    return a>b;//从大到小排序
}
//表达式函数
int f(int L)
{
    int sum=0;
    for(vector<int>::iterator it=vi.begin();it!=vi.end();it++)
    {
        sum+=*it/L;
    }
    return sum;
}
//二分法求解函数
int solve(int K)
{
    int left = 1;
    //关键点：取值必须要大于最大值
    int right = vi[0]+1;//[left,right] = [1,vi[0]+1]
    int mid=(left+right)/2;//取left与right的中点
    while(right > left)
    {
        mid = (left+right)/2;//取left与right的中点
        if(f(mid)<K) //如果求解结果比期望的小，需要减小L
        {
            right = mid;//往左子区间[left,mid]继续逼近
        }
        else
        {
            left = mid+1;//往右子区间[mid,right]继续逼近
        }
    }
    return left;//返回夹出的数值
}
//主函数
int main()
{
    int n,K;//木棒的根数、需要得到的长度相等的木棒根数
    int num,ans,sum=0;
    scanf("%d %d",&n,&K);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num);
        vi.push_back(num);
    }
    //从大到小排序
    sort(vi.begin(),vi.end(),cmp);
    ans = solve(K);
    printf("%d",ans-1);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目同样需要注意左右区间的取值范围，比如右端点初始值需要大于元素中的最大值，例如 vi[0]+1。同时，需要关注 L 和 k 之间的关系。
  • 显然，木棒切割问题和前面的装水问题都属于二分答案的做法，即对题目所求的东西进行二分，来找到一个满足所需条件的解。

快速幂

  • 先来看一个问题：
  • 给定三个整数 a、b、m（a<109a<10^9 , b<106b<10^6, 1<m<1091<m<10^9）, 求 aba^b %m。
  • 由于可能存在 aba^b 数据非常大，可能超出 int32 甚至 int64 的取值范围。
  • 因此上述问题的最简单解决方法是循环取余法，在每次操作时，就对边界进行取余操作，确保结果 ans，是在边界内的。
  • 循环取余法是一种采用数学归纳法发现数学性质并将其应用于计算机程序的重要算法！
  • 把指数操作转换成一次次的乘法，每次相乘就取以此余数，使得数值不超过范围。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <cstdio>
#include <stdio.h>
#include <stdlib.h>
typedef long long LL;
//循环取余法函数
LL pow(LL a,LL b,LL m)
{
    LL ans = 1;
    for(int i=0;i<b;i++)
    {
        ans = ans*a%m;
    }
    return ans;
}
int main() {
    LL a=2;
    LL b=3;
    LL m=3;
    LL ans;
    ans = pow(a,b,m);
    printf("%ld",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 代码中使用 long long 而不用 int 的原因是防止两个 int 变量相乘后溢出。
  • 接下来研究一个更进一步的问题：
  • 给定三个整数 a、b、m（a<109a<10^9 , b<1018b<10^{18}, 1<m<1091<m<10^9）, 求 aba^b %m。
  • 对于这个问题，如果还是按上面的做法显然是不行的，O(b)O(b) 的复杂度连支持 b<108b<10^8 都已经很困难了，更何况 101810^{18}。
  • 因此，需要介绍快速幂的做法，它基于二分的思想，因此也常称为二分幂。快速幂基于以下事实：
  1. 如果 b 是奇数，那么有 ab=a×ab−1a^b=a×a^{b-1}。
  2. 如果 b 是偶数，那么有 ab=ab2×ab2a^b=a^{\frac{b}{2}}×a^{\frac{b}{2}}。
  • 显然，b 是奇数的情况总可以在下一步转换为 b 是偶数的情况，而 b 是偶数的情况总可以在下一步转换为 b2\frac{b}{2} 的情况。这样，在 log(b)log(b) 级别次数的转换后，就可以把 b 变为 0，而任何正整数的 0 次方都是 1。
  • 举个例子，如果需要求 2102^{10}:
  1. 对 2102^{10} 来说，由于幂次 10 为偶数，因此需要先求 252^{5}，然后有 210=25×252^{10}=2^{5}×2^{5}。
  2. 对 252^{5} 来说，由于幂次 5 为奇数，因此需要先求 242^{4}，然后有 25=2×242^{5}=2×2^{4}。
  3. 对 242^{4} 来说，由于幂次 4 为偶数，因此需要先求 222^{2}，然后有 24=22×222^{4}=2^{2}×2^{2}。
  4. 对 222^{2} 来说，由于幂次 2 为偶数，因此需要先求 212^{1}，然后有 22=21×212^{2}=2^{1}×2^{1}。
  5. 对 212^{1} 来说，由于幂次 1 为奇数，因此需要先求 202^{0}，然后有 21=2×202^{1}=2×2^{0}。
  6. 20=12^{0}=1，然后从下往上依次回退计算即可。
  • 这显然是递归的思想，于是可以得到快速幂的递归写法，时间复杂度为 O(logb)O(logb):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
typedef long long LL;
//快速幂递归写法
LL binaryPow(LL a,LL b,LL m)
{
    if(b==0)
        return 1;//如果b为0，那么a^0=1
    //b为奇数，转换为b-1
    if(b%2==1)
        return a*binaryPow(a,b-1,m)%m;
    else//b为偶数，转换为b/2
    {
        LL mul = binaryPow(a,b/2,m);
        return mul * mul % m;
    }
}
  • 上面代码中，条件 if(b%2==1) 可以用 if(b&1) 代替。这是因为 b&1 进行位与操作，判断 b 的末位是否为 1，因此当 b 为奇数时 b&1 返回 1，if 条件成立。这样写的执行速度快一些。
  • 还需要注意的是：
  • 当 b%2==0 时，不要直接返回 binaryPow(a,b/2,m)*binaryPow(a,b/2,m)，而应算出单个 binaryPow(a,b/2,m) 之后再乘起来。
  • 这是因为前者每次都会调用两个 binaryPow 函数，导致 O(2log(b))=O(b)O(2^{log(b)})=O(b)。
  • 例如求 binaryPow(8) 时，会变成 binaryPow(4)*binaryPow(4)，而这两个 binaryPow(4) 都会各自变成 binaryPow(2)*binaryPow(2)，于是就需要求四次 binaryPow(2)；
  • 而每个 binaryPow(2) 又会变成 binaryPow(1)*binaryPow(1)，因此最后需要求八次 binaryPow(1)。
  • 另外，针对不同的题目，可能有两个细节需要注意：
  1. 如果初始时 a 有可能大于等于 m，那么需要在进入函数前就让 a 对 m 取模。
  2. 如果 m 为 1，可以直接在函数外部特例判 0，不需要进入函数来计算（因为任何正整数对 1 取模一定等于 0）。

  • 接下来研究一下快速幂的迭代写法：

  • 对 aba^b 来说，如果把 b 写出二进制，那么 b 就可以写成若干二次幂之和。

  • 例如 13 的二进制是 1101，于是 3 号位、2 号位、0 号位都是 1，那么就可以得到 13=23+22+20=8+4+113=2^3+2^2+2^0=8+4+1，所有 a13=a8+4+1=a8×a4×a1a^{13}=a^{8+4+1}=a^8×a^4×a^1。

  • 通过上面的推导，我们发现 a13a^{13} 可以表示成 a8a^{8}、a4a^{4}、a1a^{1} 的乘积。

  • 因此，通过同样的推导，我们可以把任意的 aba^b 表示成 a2ka^{2^k} 、……、a8a^{8}、a4a^{4}、a2a^{2}、a1a^{1} 中若干项的乘积，其中如果 b 的二进制 i 号位为 1，那么项 a2ia^{2^i} 就被选中。

  • 于是可以得到计算 aba^b 的大致思路：令 i 从 0 到 k 枚举 b 的二进制的每一位，如果当前位为 1，那么累积 a2ia^{2^i}。

  • 注意到序列 a2ka^{2^k} 、……、a8a^{8}、a4a^{4}、a2a^{2}、a1a^{1} 的前一项总是等于后一项的平方，因此具体实现的时候可以用如下方式：

  • ①初始令 ans 等于 1，用来存放累积的结果。

  • ②判断 b 的二进制末尾是否为 1（即判断 b&1 是否为 1，也可以理解为判断 b 是否为奇数），如果是的话，令 ans 乘上 a 的值。

  • ③令 a 平方，并将 b 右移一位（也可以理解为将 b 除以 2）。

  • ④只要 b 大于 0，就返回②。

  • 快速幂的迭代算法代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef long long LL;
//快速幂迭代写法
LL binaryPow_2(LL a,LL b,LL m)
{
    LL ans = 1;
    while(b>0)
    {
        if(b&1)//如果b的二进制末尾为1(也可以写成if(b%2))
        {
            ans = ans*a%m;//令ans累计上a
        }
        a = a*a%m;//令a平方
        b>>=1;//将b的二进制右移一位，b=b>>1或b/2
    }
    return ans;
}
  • 在实际使用上，递归写法和迭代写法在效率上的差别并不明显。
  • 当 b 等于 13 时，可以得到图 4-7 的模拟过程：

双指针 (two pointers)

什么是双指针 (two pointers)

  • 双指针 (two pointers) 是算法编程中一种非常重要思想，其思想十分简洁，但却提供了非常高的算法效率。
  • 以一个例子引入：
  • 给定一个递增的正整数序列和一个正整数 M,求序列中两个不同位置的数 a 和 b，使得它们的和恰好为 M，输出所有满足条件的方案。
  • 例如给定序列 {1,2,3,4,5,6} 和正整数 M=8，就存在 2+6=82+6=8、3+5=83+5=8 成立。
  • 其中最直观的做法是使用二重循环枚举序列中的整数 a 和 b，判断它们的和是否为 M，如果是，输出方案；如果不是，则继续枚举。代码如下：
1
2
3
4
5
6
7
8
9
10
for(int i=0;i<n;i++)
{
	for(int j=i+1;j<n;j++)
	{
		if(a[i]+a[j]==M)
		{
			printf("%d %d\n",a[i],a[j]);
		}
	}
}
  • 显然，这种做法的时间复杂度为 O(n2)O(n^2)，对 n 在 10510^5 的规模时是不可接受的。
  • 其中产生高复杂度的原因如下：
  1. 对于一个确定的 a[i] 来说，如果当前的 a[i] 满足 a[i]+a[j]>M，显然也会有 a[i]+a[j+1]>M 成立（这是由于序列是递增的），因此不需要对 a[j] 之后的数进行枚举。
  2. 对于某个 a[i] 来说，如果找到一个 a[j]，使得 a[i]+a[j]>M 恰好成立，那么对 a[i+1] 来说，一定也有 a[i+1]+a[j]>M 成立，因此 a[i] 之后的元素也不必再去枚举。
  • 上面两点体现了一个问题：
  • i 和 j 的枚举是相互牵制的，而这可以给优化算法带来很大的空间。
  • 事实上，本题中双指针 (two pointers)将利用有序序列的枚举特性来有效降低复杂度，其算法过程如下：
  • 令下标 i 的初值为 0，下标 j 的初值为 n-1，即令 i、j 分别指向序列的第一个元素和最后一个元素，接下来根据 a[i]+a[j] 与 M 的大小来进行下面三种选择，使 i 不断向右移动、使 j 不断向左移动，直到 i≥j 成立，如下图 4-8 所示：

  1. 如果满足 a[i]+a[j]==M，说明找到了其中一组方案。由于序列递增，不等式 a[i+1]+a[j]>M 与 a[i]+a[j-1]<M 均成立，但是 a[i+1]+a[j-1] 与 M 的大小未知，因此剩余方案只可能在 [i+1,j-1] 区间内产生，令 i=i+1、j=j-1（即令 i 向右移动，j 向左移动）；
  2. 如果满足 a[i]+a[j]>M，由于序列递增，不等式 a[i+1]+a[j]>M 成立，但是 a[i]+a[j-1] 与 M 的大小未知，因此剩余方案只可能在 [i,j-1] 区间内产生，令 j=j-1（即令 j 向左移动）；
  3. 如果满足 a[i]+a[j]<M，由于序列递增，不等式 a[i]+a[j-1]<M 成立，但是 a[i+1]+a[j] 与 M 的大小未知，因此剩余方案只可能在 [i+1,j] 区间内产生，令 i=i+1（即令 i 向左移动）。
  • 反复执行上面三个判断，直到 i≥j 成立，例题如下

例题：2-SUM-双指针

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
using namespace std;
const int MAX = 100010;
//解决函数
int solve(int A[],int n,int k)
{
    int i=0,j=n-1;
    int num=0;
    while(i<j)
    {
        if(A[i]+A[j]==k)
        {
            num++;
            i++;
            j--;
        }
        else if(A[i]+A[j]>k)
        {
            j--;
        }
        else
        {
            i++;
        }
    }
    return num;
}
//主函数
int main()
{
    int n,k,ans;
    int A[MAX];
    scanf("%d %d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    ans=solve(A,n,k);
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 下面来分析上述算法的复杂度：
  • 由于 i 的初值为 0，j 的初值为 n-1，而程序中变量 i 只有递增操作、变量 j 只有递减操作，且循环当 i≥j 时停止，因此 i 和 j 的操作次数最多为 n 次，时间复杂度为 O(n)O(n)。
  • 不难看出，双指针 (two pointers)的思想充分利用了序列递增的性质，以较为浅显的思想降低了复杂度。
  • 接下来看序列合并问题：
  • 假设有两个递增序列 A 与 B，要求将它们合并为一个递增序列 C。
  • 同样的，可以设置两个下标 i 和 j，初值均为 0，表示分别指向序列 A 的第一个元素和序列 B 的第一个元素，然后根据 A[i] 与 B[j] 的大小来决定哪一个放入序列 C。
  1. 若 A[i]<B[j]，说明 A[i] 是当前序列 A 与序列 B 的剩余元素中最小的那个，因此把 A[i] 加入序列 C 中，并让 i=i+1（即让 i 右移一位）；
  2. 若 A[i]>B[j]，说明 B[j] 是当前序列 A 与序列 B 的剩余元素中最小的那个，因此把 B[j] 加入序列 C 中，并让 j=j+1（即让 j 右移一位）；
  3. 若 A[i]==B[j]，则任意选一个加入到序列 C 中，并让对应下标加 1。
  • 上面的分支操作直到 i、j 中的一个到达序列末端为止，然后将另一个序列的所有元素依次加入到序列 C 中。

例题：序列合并

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
using namespace std;
const int MAX1 = 100010;
const int MAX2 = 200010;
//解决函数
int solve(int A[],int B[],int C[],int n,int m)
{
    int i=0,j=0,index=0;
    while(i<n&&j<m)
    {
        if(A[i]<B[j])
            C[index++]=A[i++];
        else
            C[index++]=B[j++];
    }
    while(i<n)
    {
        C[index++]=A[i++];
    }
    while(j<m)
    {
        C[index++]=B[j++];
    }
    return index;//返回序列C的长度
}
//主函数
int main()
{
    int n,m;
    int A[MAX1],B[MAX1];
    int C[MAX2];
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    for(int i=0;i<m;i++)
    {
        scanf("%d",&B[i]);
    }
    int index;//序列C的长度
    index = solve(A,B,C,n,m);
    for(int i=0;i<index;i++)
    {
        printf("%d",C[i]);
        if(i<index-1)
            printf(" ");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 双指针 (two pointers)是怎样一种思想？
  • 事实上，双指针 (two pointers)最原始的含义就是针对本节的第一个问题而言的，而广义上双指针 (two pointers)则是利用问题本身与序列的特性，使用两个下标 i、j 对序列进行扫描（可以同向扫描，也可以反向扫描），以较低的复杂度（一般是 O(n)O(n) 的复杂度）解决问题。

归并排序

  • 归并排序是一种基于“归并”思想的排序方法， 主要介绍其中最基本的 2-路归并排序。
  • 2-路归并排序的原理是：将序列两两分组，将序列归并为 [n2][\frac{n}{2}] 个组，组内单独排序；
  • 然后将这些组再两两归并，生成 [n4][\frac{n}{4}] 个组，组内再单独排序；
  • 以此类推，直到只剩下一个组为止。归并排序的时间复杂度为 O(nlogn)O(nlogn)。
  • 下面来看一个例子：将序列 {66,12,33,57,64,27,18} 进行 2-路归并排序。
  • ①第一趟，两两分组，得到四组：{66,12}、{33,57}、{64,27}、{18}，组内单独排序，得到新序列 {{12,66},{33,57},{27,64},18}\{\{12,66\},\{33,57\},\{27,64\},18\};
  • ②第二趟，将四个组继续两两分组，得到两组：{12,66,33,57} 和 {27,64,18}，组内单独排序，得到新序列 {{12,33,57,66},{18,27,64}}\{\{12,33,57,66\},\{18,27,64\}\};
  • ③ 第三趟，将两个组继续两两分组，得到一组：{12,33,57,66,18,27,64}，组内单独排序，得到新序列 {12,18,27,33,57,64,66}\{12,18,27,33,57,64,66\}，算法结束！
  • 整个过程如下图 4-9 所示：

  • 从上面的过程中可以发现，2-路归并排序的核心在于如何将两个有序序列合并为一个有序序列，这一过程在上一小节“序列合并问题”中已经有所探讨。
  • 接下来讨论 2-路归并排序的递归版本和非递归版本的具体实现。
  1. 递归版本
  • 2-路归并排序的递归写法非常简单，只需要反复将当前区间 [left,right] 分为两半，对两个子区间 [left,mid] 与 [mid+1,right] 分别递归进行归并排序，然后将两个已经有序的子区间合并为有序序列即可, 例题如下：

例题：归并排序

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
using namespace std;
const int MAX1 = 100010;
const int MAXN = 1000;
//合并函数
//将数组A的[L1,R1]与[L2,R2]区间合并为有序区间(此处L2即为R1+1)
void merge(int A[],int L1,int R1,int L2,int R2)
{
    int i=L1,j=L2;//i指向A[L1],j指向A[L2]
    int temp[MAXN],index=0;//temp临时存放合并后的数组，index为其下标
    while(i<=R1&&j<=R2)
    {
        if(A[i]<=A[j])
        {
            temp[index++]=A[i++];
        }
        else
        {
            temp[index++]=A[j++];
        }
    }
    while(i<=R1)
    {
        temp[index++]=A[i++];
    }
    while(j<=R2)
    {
        temp[index++]=A[j++];
    }
    for(int i=0;i<index;i++)
    {
        A[L1+i]=temp[i];//将合并后的序列赋值回数组A
    }
}
//将array数组当前区间[left,right]进行归并排序
void mergeSort(int A[],int left,int right)
{
    if(left<right)//只要left小于right
    {
        int mid=(left+right)/2;//取中点
        mergeSort(A,left,mid);//递归，将左子区间[left,mid]归并排序
        mergeSort(A,mid+1,right);//递归，将右子区间[mid+1,right]归并排序
        merge(A,left,mid,mid+1,right);//将左子区间和右子区间合并
    }
}
//主函数
int main()
{
    int A[MAX1];
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    mergeSort(A,0,n-1);
    for(int i=0;i<n;i++)
    {
        printf("%d",A[i]);
        if(i<n-1)
            printf(" ");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  1. 非递归版本
  • 2-路归并排序的的非递归实现主要考虑这样一点: 每次分组时组内元素个数上限都是 2 的幂次。
  • 于是可以得到这样的思路：
  • 令步长 step 的初值为 2，然后将数组中每 step 个元素作为一组，将其内部进行排序（即把左 step2\frac{step}{2} 个元素与右 step2\frac{step}{2} 个元素合并，若元素个数不超过 step2\frac{step}{2}，则不操作）
  • 再令 step 乘 2，重复上面的操作，直到 step2\frac{step}{2} 超过元素个数 n，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//非递归版本归并排序法
void mergeSort2(int A[],int n)
{
    //step为组内元素个数，step/2为左子区间元素个数，注意等号可以不取
    for(int step=2;step/2<n;step*=2)
    {
        //每step个元素一组，组内前step/2和step/2个元素进行合并
        for(int i=0;i<n;i+=step)//对每一组
        {
            int mid = i+step/2-1;//左子区间元素个数为step/2
            if(mid+1<n)//右子区间如果存在元素就合并
            {
                //左子区间为[i,mid],右子区间为[mid+1,min(i+step-1,n-1)]
                merge(A,i,mid,mid+1,min(i+step-1,n-1));//将左子区间和右子区间合并
            }
        }
    }
}
  • 如果题目中要求给出归并排序每一趟结束时的序列，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//非递归版本归并排序法
void mergeSort2(int A[],int n)
{
    //step为组内元素个数，step/2为左子区间元素个数，注意等号可以不取
    for(int step=2;step/2<n;step*=2)
    {
        //每step个元素一组，组内前step/2和step/2个元素进行合并
        for(int i=0;i<n;i+=step)//对每一组
        {
            int mid = i+step/2-1;//左子区间元素个数为step/2
            if(mid+1<n)//右子区间如果存在元素就合并
            {
                //左子区间为[i,mid],右子区间为[mid+1,min(i+step-1,n-1)]
                merge(A,i,mid,mid+1,min(i+step-1,n-1));//将左子区间和右子区间合并
            }
        }
        //输出归并排序的某一趟结束的序列
        for(int i=0;i<n;i++)
        {
            printf("%d",A[i]);
            if(i<n-1)
                printf(" ");
        }
        printf("\n");
    }
}
  • 也完全可以使用 sort() 函数来代替 merge() 函数（只要时间限制允许）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//非递归版本归并排序法(sort()函数使用)
void mergeSort3(int A[],int n)
{
    //step为组内元素个数，step/2为左子区间元素个数，注意等号可以不取
    for(int step=2;step/2<n;step*=2)
    {
        //每step个元素一组，组内[i,min(i+step,n)]进行排序
        for(int i=0;i<n;i+=step)//对每一组
        {
            sort(A+i,A+min(i+step,n));
        }
        //输出归并排序的某一趟结束的序列
        for(int i=0;i<n;i++)
        {
            printf("%d",A[i]);
            if(i<n-1)
                printf(" ");
        }
        printf("\n");
    }
}

快速排序

  • 快速排序是排序算法中平均时间复杂度为 O(nlogn)O(nlogn) 的一种算法，其实现需要先解决这样一个问题：
  • 对一个序列 A[1]、A[2]、……、A[n]，调整序列中元素的位置，使得 A[1]（原序列的 A[1]，下同）的左侧所有元素都不超过 A[1]、右侧所有元素都大于 A[1]。
  • 例如对序列 {5,3,9,6,4,1} 来说，可以调整序列中元素的位置，形成序列 {3,1,4,5,9,6}，这样就让 A[1]=5 左侧的所有元素都不超过它、右侧所有元素都大于它，如下图 4-10 所示：

  • 对这个问题来说可能会有多种方案，下面给出速度最快的做法，思想是双指针 (two pointers)：
  • ① 先将 A[1] 存至某个临时变量 temp，并令两个下标 left、right 分别指向序列首尾（如令 left=1、right=n）。
  • ② 只要 right 指向的元素 A[right] 大于 temp，就将 right 不断左移；当某个时候 A[right]≤temp 时，将元素 A[right] 挪到 left 指向的元素 A[left] 处。
  • ③ 只要 left 指向的元素 A[left] 不超过 temp，就将 left 不断右移；当某个时候 A[left]>temp 时，将元素 A[left] 挪到 right 指向的元素 A[right] 处。
  • ④ 重复②和③，直到 left 与 right 相遇，把 temp（也即原 A[1]）放到相遇的地方。
  • 为了使上面的过程更清晰，下面举一个例子：
  • 现有序列 A[1~11]={35,18,16,72,24,65,12,88,46,28,55}，调整元素位置，使得元素 A[1]=35 的左侧所有元素均不超过 35、右侧所有元素均大于 35。
  • ① 将 A[1]=35 存到临时变量 temp，并令下标 left，right 指向序列首尾（left=1、right=11）

  • ② 只要 A[right]>35 时, 就把 right 不断左移。该操作当 right==10 时满足 A[right]=28<35 , right 停止左移。之后把 A[right] 移至 A[left] 处。

  • ③ 只要 A[left]≤35 时, 就把 left 不断右移。该操作当 left==4 时满足 A[left]=72>35，left 停止右移，之后把 A[left] 移至 A[right] 处。

  • ④ 只要 A[right]>35 时, 就把 right 不断左移。该操作当 right==7 时满足 A[right]=12<35 , right 停止左移。之后把 A[right] 移至 A[left] 处。

  • ⑤ 只要 A[left]≤35 时, 就把 left 不断右移。该操作当 left==6 时满足 A[left]=65>35，left 停止右移，之后把 A[left] 移至 A[right] 处。

  • ⑥ 只要 A[right]>35 时, 就把 right 不断左移。该操作的过程中 left 与 right 在 A[6] 处相遇，将 temp=35 放到 A[6] 处，算法结束！

  • 因此可以很容易写出这部分代码，其中用以划分区间的元素 A[left] 被称为主元：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//对区间[left,right]进行划分
int partition(int A[],int left,int right)
{
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}
  • 接下来就可以正式实现快速排序算法，其思路如下：
  1. 调整序列中的元素，使当前序列最左端的元素在调整后满足左侧所有元素均不超过该元素、右侧所有元素均大于该元素。
  2. 对该元素的左侧和右侧分别递归进行步骤 1的调整，直到当前调整区间的长度不超过 1。
  • 快速排序的递归实现如下：
1
2
3
4
5
6
7
8
9
10
11
//快速排序，left与right初值为序列首尾下标(例如1和n)
void quickSort(int A[],int left,int right)
{
    if(left<right)//当前区间长度不超过1
    {
        //将[left,right]按照A[left]一分为二
        int pos = partition(A,left,right);
        quickSort(A,left,pos-1);//对左子区间递归进行快速排序
        quickSort(A,pos+1,right);//对右子区间递归进行快速排序
    }
}
  • 快速排序算法当序列中元素的排列比较随机时效率最高，但是当序列中元素接近有序时，会达到最坏时间复杂度 O(n2)O(n^2)。产生这种情况的主要原因在于主元没有把当前区间划分为两个长度接近的子区间。
  • 那么如何解决这个问题？
  • 其中一个办法是随机选择主元，也就是对 A[left……right] 来说，不总用 A[left] 作为主元，而是从 A[left]、A[left+1]、……、A[right] 中随机选择一个数据作为主元。
  • 这样虽然算法的最坏时间复杂度仍然是 O(n2)O(n^2)（例如，总是选择了 A[left] 作为主元），但是对任意输入数据的期望时间复杂度都能达到 O(nlogn)O(nlogn)，也就是说，不存在一组特定的数据能使这个算法出现最坏的情况（证明参考《算法导论》）！
  • 接下来讨论如何生成随机数：
  • 在 C 语言中有可以产生随机数据的函数，需要添加 #include <stdlib.h> 头文件与 #include <time.h> 头文件。
  • 首先在 main 函数开头加上 srand((unsigned)time(NULL));，这个语句将生成随机数种子（srand 用于初始化随机种子）。
  • 然后在需要使用随机数的地方使用 rand() 函数，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <time.h>
using namespace std;
//主函数
int main()
{
    srand((unsigned)time(NULL));//随机数种子
    for(int i=0;i<10;i++)
    {
        printf("%d ",rand());
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
14678 12133 31822 15298 12428 1961 13586 23306 19257 20059
  • 显然输出结果肯定是实时变化的，上面的结果只是一个举例。
  • 同时，我们应该还须知道，rand() 函数只能输出 [0, RAND_MAX] 范围内的整数（RAND_MAX 是 #include <stdlib.h> 头文件，在不同系统环境中，该常数的值有所不同，此处使用的是 32767），因此如果想要输出给定范围 [a,b] 内随机数，需要使用 rand()%(b-a+1)+a。
  • 显然 rand()%(b-a+1) 的范围是 [0, b-a],再加上 a 之后就是 [a,b]。例如下面的代码生成 [0,1] 与 [3,7] 范围内的随机数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <time.h>
using namespace std;
//主函数
int main()
{
    int a,b;
    srand((unsigned)time(NULL));//随机数种子
    //[0,1]
    a=0,b=1;
    for(int i=0;i<10;i++)
    {
        printf("%d ",rand()%(b-a+1)+a);
    }
    printf("\n");
    //[3,7]
    a=3,b=7;
    for(int i=0;i<10;i++)
    {
        printf("%d ",rand()%(b-a+1)+a);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2
1 0 0 0 0 0 1 1 0 1
4 5 4 5 6 6 3 5 3 6
  • 不难发现，这种做法只对相差不超过 RAND_MAX 的区间的随机数有效，如果需要生成更大的数（例如 [a,b]，b 大于 RAND_MAX=32767 ）就不行了。
  • 想要生成大范围的随机数有很多方法，例如可以多次生成 rand() 随机数，然后用位运算拼接起来（或者直接将 rand() 随机数相乘）；也可以随机选每一个数位的值 (0~9)，然后拼接成一个大整数；
  • 当然，也可以采用另一种思路：
  • 先用 rand() 函数生成一个 [0, RAND_MAX] 范围内的随机数，然后用这个随机数除以 RAND_MAX，这样就会得到一个 [0,1] 范围内的浮点数。我们只需要用这个浮点数乘以范围长度 (b-a+1),再加上 a 即可，即 (int)((double)rand()/RAND_MAX*(b-a+1)+a)，相当于这个浮点数就是 [a,b] 范围内的比例位置，代码示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <time.h>
using namespace std;
//主函数
int main()
{
    int a,b;
    srand((unsigned)time(NULL));//随机数种子
    //[10000,60000]
    a=10000,b=60000;
    for(int i=0;i<10;i++)
    {
        printf("%d ",(int)((double)rand()/RAND_MAX*(b-a+1)+a));
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
42205 55224 53408 43784 52908 54687 27203 55163 22528 28393
  • 在此基础上继续讨论快排的写法：
  • 由于现在需要在 A[left……right] 中随机选取一个主元，因此不妨生成一个范围在 [left,right] 内的随机数 p，然后以 A[p] 作为主元来进行划分。具体做法是将 A[p] 与 A[left] 交换
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//对区间[left,right]进行划分
int partition(int A[],int left,int right)
{
    //生成[left,right]内的随机数p
    srand((unsigned)time(NULL));//随机数种子
    int p = (int)((double)rand()/RAND_MAX*(right-left+1)+left);
    swap(A[p],A[left]);//交换A[p]和A[left]
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}

例题：快速排序

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <time.h>
using namespace std;

const int MAX = 1010;

//对区间[left,right]进行划分
int partition(int A[],int left,int right)
{
    //生成[left,right]内的随机数p
    srand((unsigned)time(NULL));//随机数种子
    int p = (int)((double)rand()/RAND_MAX*(right-left+1)+left);
    swap(A[p],A[left]);//交换A[p]和A[left]
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}

//快速排序，left与right初值为序列首尾下标(例如1和n)
void quickSort(int A[],int left,int right)
{
    if(left<right)//当前区间长度不超过1
    {
        //将[left,right]按照A[left]一分为二
        int pos = partition(A,left,right);
        quickSort(A,left,pos-1);//对左子区间递归进行快速排序
        quickSort(A,pos+1,right);//对右子区间递归进行快速排序
    }
}

//主函数
int main()
{
    int n,A[MAX];
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    quickSort(A,0,n-1);
    for(int i=0;i<n;i++)
    {
        printf("%d",A[i]);
        if(i<n-1)
            printf(" ");
    }
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

双指针 (two pointers)例题

例题：集合求差III、集合求差IV

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <string>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
using namespace std;

const int MAX1 = 100010;
const int MAX2 = 200010;

//解决函数
int solve(int A[],int B[],int C[],int n,int m)
{
    int i=0,j=0,index=0;
    while(i<n&&j<m)
    {
        if(A[i]<B[j])
            C[index++]=A[i++];
        else if(A[i]>B[j])
            j++;
        else
        {
            i++;
            j++;
        }
    }
    while(i<n)
            C[index++]=A[i++];
    return index;//返回序列C的长度
}

//主函数
int main()
{
    int n,m;
    int A[MAX1],B[MAX1];
    int C[MAX2];
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);
    }
    for(int i=0;i<m;i++)
    {
        scanf("%d",&B[i]);
    }
    int index;//序列C的长度
    index = solve(A,B,C,n,m);
    for(int i=0;i<index;i++)
    {
        printf("%d",C[i]);
        if(i<index-1)
            printf(" ");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：
  • 这两道题目可以共用一套代码，主要思路在于：
  • 如果数组 A[i]<B[j] 就把 A[i] 加入到 C 数组中；
  • 如果 A[i]>B[j] 就把指针 j 右移；
  • 如果 A[i]==B[j] 就把指针 j 和 i 都右移；
  • 最后把数组 A 中剩余的数据全部加入到数组 C 中即可!

其它高效技巧与算法

  • 前面几节介绍了一些最常用的算法思想，下面介绍其它高效技巧与算法。

打表

  • 打表是一种典型的用空间换时间的技巧，一般指将所有可能用到的结果实现计算出来，这样后面需要用到的时候直接查表获得。
  • 打表常见的用法有如下几种：
  1. 在程序中一次性计算出所有需要用到的结果，之后通过查询直接取这些结果。
  • 这个是最常用到的用法，例如在一个需要查询大量 Fibonacci 数 F(n) 的问题中，显然每次从头开始计算是非常耗时的，对 Q 次查询会产生 O(nQ)O(nQ) 的时间复杂度；
  • 而如果进行预处理，即把所有 Fibonacci 数预先计算并存在数组中，那么每次查询就只需要 O(1)O(1) 的时间复杂度，对 Q 次查询就只需要 O(n+Q)O(n+Q) 的时间复杂度（其中 O(n)O(n) 是预处理的时间）。
  1. 在程序 B 分一次或多次计算出所有需要用到的结果，手工把结果写在程序 A 的数组中，然后在程序 A 中就可以直接使用这些结果。
  • 这种用法一般是当程序的一部分过程消耗的时间过多，或是没有想到好的算法，因此在另一个程序中使用暴力算法求出结果，这样就能直接在原程序中使用这些结果。
  • 例如对 n 皇后问题来说，如果使用的算法不好，就容易超时，而可以在本地用程序计算出对所有 n 来说的 n 皇后方案数，然后把算出的结果直接写在数组中，就可以根据题目输入的 n 来直接出结果。
  1. 对一些感觉不会做的题目，先用暴力程序计算小范围数据的结果，然后找规律，或许就能发现一些“蛛丝马迹”。
  • 这种用法在数据范围非常大时容易用到，因为这样的题目可能不是用直接能想到的算法来解决的，而需要寻找一些规律才能得到结果。

活用递推

  • 有很多题目需要细心考虑过程中是否可能存在递推关系，如果能找到这样的递推关系，就能够使时间复杂度下降不少。
  • 例如就一类涉及序列的题目来说，假如序列的每一位所需要计算的值都可以通过该位左右两侧的结果计算得到，那么就可以考虑所谓的“左右两侧的结果”是否能通过递推进行预处理得到，这样在后面就不必反复求解。

例题：PAT B1040、PAT A1093

  • 思路：
  • 本题直接进行暴力求解会超时；
  • 因此需要换一个角度思考，对于一个确定位置的字符 A 来说，以它形成的 PAT 的个数等于它左边 P 的个数乘以它右边 T 的个数。
  • 例如对于字符串 APPAPT 的中间那个字符 A 来说，它左边有两个 P，右边有一个 T，因此这个 A 能形成的 PAT 的个数就是 2×1=22×1=2。
  • 于是问题就转换为，对于字符串中的每个 A，计算它左边 P 的个数与它右边 T 的个数的乘积，然后把所有 A 的这个乘积相加就是答案。
  • 如何比较快地获得每一位左边 P 的个数？
  • 只需要设定一个数组 int leftNumP[MAX]，使用变量 numP 记录每一位左边 P 的个数（含当前位，下同）。于是只需要 O(len)O(len) 的时间复杂度就能统计出 leftNumP 数组。
  • 以同样的方法可以计算出每个字符 A 右边 T 的个数。
  • 为了节省代码量,不妨在统计每个字符 A 右边 T 的个数的过程中直接计算答案 ans。
  • 具体做法是：
  • 定义一个变量 numT，记录当前累计右边 T 的个数。从右往左遍历字符串，如果当前位 i 是字符 T，那么令变量 numT++;。
  • 否则，如果当前位 i 是 A，那么令 ans=(ans+leftNumP[i]*numT)%MOD;！
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
using namespace std;

const int MAX = 100010;
const int MOD = 1000000007;

//变量定义
int leftNumP[MAX] = {0};
string str;

//主函数
int main()
{
    cin >> str;//读入字符串
    int len = str.length();
    int numP = 0,numT = 0;
    int ans = 0;
    for(int i=0;i<len;i++)
    {
        if(str[i]=='P')
            numP++;
        else if(str[i]=='A')
        {
            leftNumP[i]=numP;
        }
    }
    for(int i=len-1;i>=0;i--)
    {
        if(str[i]=='T')
            numT++;
        else if(str[i]=='A')
        {
            ans = (ans+leftNumP[i]*numT)%MOD;
        }
    }
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

例题：PAT B1045、PAT A1101

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
using namespace std;

const int MAX = 100010;

//主函数
int main()
{
    int n;
    int num[MAX];
    int num1[MAX]={0};
    int num2[MAX]={0};
    int index=0,my_max=INT_MIN,my_min=INT_MAX;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num[i]);
    }
    for(int i=n-1;i>=0;i--)
    {
        my_min = min(num[i],my_min);
        if(my_min==num[i])
        {
            num1[i]=my_min;
        }
    }
    for(int i=0;i<n;i++)
    {
        my_max = max(num[i],my_max);
        if(my_max==num[i]&&num1[i]!=0)
        {
            num2[index++]=num[i];
        }
    }
    printf("%d\n",index);
    for(int i=0;i<index;i++)
    {
        printf("%d",num2[i]);
        if(i<index-1)
            printf(" ");
    }
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：本题与上面例题《有几个PAT》思路较为相似，注意认真体会这两道题目的思想。

随机选择算法

  • 本节主要讨论这样一个问题：如何从一个无序的数组中求出第 K 大的数（为了简化讨论，假设数组中的数各不相同）。
  • 例如，对数组 {5,12,7,2,9,3} 来说，第三大数是 5，第五大数是 9。
  • 最直接的想法是对数组进行排序，然后直接取出第 K 个元素即可。但是这样的做法需要 O(nlogn)O(nlogn) 的时间复杂度，虽然看起来很好，但是还有更优的算法。
  • 下面介绍随机选择算法，它对任何输入都可以达到 O(n)O(n) 的期望时间复杂度。
  • 随机选择算法的原理类似于随机快速排序算法。
  • 当对 A[left,right] 执行一次 randPartition() 函数之后，主元左侧的元素个数就是确定的，且它们都是小于主元。randPartition() 函数代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//对区间[left,right]进行划分
int randPartition(int A[],int left,int right)
{
    //生成[left,right]内的随机数p
    srand((unsigned)time(NULL));//随机数种子
    int p = (int)((double)rand()/RAND_MAX*(right-left+1)+left);
    swap(A[p],A[left]);//交换A[p]和A[left]
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}
  • 假设此时主元是 A[p]，那么 A[p] 就是 A[left,right] 中的第 p-left+1 大的数。
  • 不妨令 M 表示 p-left+1，那么如果 K==M 成立，说明第 K 大的数就是主元 A[p]；
  • 如果 K<M 成立，就说明第 K 大的数在主元左侧，即 A[left……(p-1)] 中的第 K 大，往左侧递归即可；
  • 如果 K>M 成立，则说明第 K 大的数在主元右侧，即 A[(p+1)……right] 中的第 K-M 大，往右侧递归即可。
  • 算法以 left==right 作为递归边界，返回 A[left]，由此可以写出随机选择算法的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//随机选择算法，从A[left,right]中返回第K大的数
int randSelect(int A[],int left,int right,int K)
{
    if(left==right)
        return A[left];//边界
    int p = randPartition(A,left,right);//划分后主元的位置p
    int M = p-left+1;//A[p]是A[left,right]中的第M大
    if(K==M)
        return A[p];//找到第K大的数
    else if(K<M)//第K大的数在主元左侧
        return randSelect(A,left,p-1,K);//往主元左侧找第K大
    else//第K大的数在主元右侧
        return randSelect(A,p+1,right,K-M);//往主元右侧找第K-M大
}
  • 可以证明，虽然随机选择算法的最坏时间复杂度是 O(n2)O(n^2)，但是其对任意输入的期望时间复杂度却是 O(n)O(n)，这意味着不存咋一组特定的数据能使这个算法出现最坏的情况，是个相当实用和出色的算法（详细证明参考《算法导论》）。
  • 下面的问题是一个应用：
  • 给定一个由整数组成的集合，集合中的整数各不相同，现在要将它们分为两个子集合，使得这两个子集合的并集为原集合、交集为空集，同时在两个子集合的元素个数 n1n_1 与 n2n_2 之差的绝对值 ∣n1−n2∣|n_1-n_2| 尽可能小的前提下，要求它们各自的元素之和 S1S_1 与 S2S_2 之差的绝对值 ∣S1−S2∣|S_1-S_2| 尽可能大，求这个 ∣S1−S2∣|S_1-S_2| 等于多少。
  • 不难发现，如果原集合中元素个数为 n，那么当 n 是偶数时，由它分出的两个子集合中的元素个数都是 n2\frac{n}{2}；
  • 如果 n 是奇数时，由它分出的两个子集合中的元素个数分别是 n2\frac{n}{2} 和 n2+1\frac{n}{2}+1。
  • 显然，为了使 ∣S1−S2∣|S_1-S_2| 尽可能大，最直接的思路是将原集合的元素从小到大排序，取排序后的前 n2\frac{n}{2} 个元素作为其中一个子集合，剩下的元素作为另一个子集合即可，时间复杂度为 O(nlogn)O(nlogn)。
  • 而更优的做法是使用上述随机选择算法。根据对问题的分析，上述问题实际上就是求原集合中元素的第 n2\frac{n}{2} 大，同时根据这个数把集合分为两部分，使得其中一个子集合中的元素都不小于这个数，而另一个子集合中的元素都大于这个数，至于两个子集合内部元素的顺序则不需要关心。
  • 因此只需要使用 randSelect() 函数求出 n2\frac{n}{2} 大的数即可，该函数会自动切分好两个集合，期望时间复杂度为 O(n)O(n)，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
using namespace std;

const int MAX = 100010;

//对区间[left,right]进行划分
int randPartition(int A[],int left,int right)
{
    //生成[left,right]内的随机数p
    srand((unsigned)time(NULL));//随机数种子
    int p = (int)((double)rand()/RAND_MAX*(right-left+1)+left);
    swap(A[p],A[left]);//交换A[p]和A[left]
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}

//随机选择算法，从A[left,right]中返回第K大的数
int randSelect(int A[],int left,int right,int K)
{
    if(left==right)
        return A[left];//边界
    int p = randPartition(A,left,right);//划分后主元的位置p
    int M = p-left+1;//A[p]是A[left,right]中的第M大
    if(K==M)
        return A[p];//找到第K大的数
    else if(K<M)//第K大的数在主元左侧
        return randSelect(A,left,p-1,K);//往主元左侧找第K大
    else//第K大的数在主元右侧
        return randSelect(A,p+1,right,K-M);//往主元右侧找第K-M大
}

//主函数
int main()
{
    int A[MAX],n;
    //sum和sum1记录所有整数之和与切分后前n/2个元素之和
    int sum=0,sum1=0;
    scanf("%d",&n);//整数个数
    for(int i=0;i<n;i++)
    {
        scanf("%d",&A[i]);//输入整数
        sum+=A[i];//累计所有整数之和
    }
    randSelect(A,0,n-1,n/2);
    for(int i=0;i<n/2;i++)
    {
        sum1+=A[i];//累计较小的子集合中的元素之和
    }
    printf("%d\n",(sum-sum1)-sum1);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输入：
1
2
13
1 6 33 18 4 0 10 5 12 7 2 9 3
  • 输出：
1
80
  • 由于在这个问题中不需要关系第 n2\frac{n}{2} 大的数是什么，而只需要实现根据第 n2\frac{n}{2} 大的数进行切分的功能，因此 randSelect() 函数不需要设置返回值。
  • 另外，如果能保证数据分布较为随机，那么代码中的 randSelect() 函数也可以替换成普通的 partition() 函数，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//对区间[left,right]进行划分
int partition(int A[],int left,int right)
{
    //生成[left,right]内的随机数p
    srand((unsigned)time(NULL));//随机数种子
    int p = (int)((double)rand()/RAND_MAX*(right-left+1)+left);
    swap(A[p],A[left]);//交换A[p]和A[left]
    int temp = A[left];//将A[left]存至临时变量temp
    while(left<right)//只要left与right不相遇
    {
        while(left<right&&A[right]>temp)
            right--;//反复左移right
        A[left] = A[right];//将A[right]挪到A[left]
        while(left<right&&A[left]<=temp)
            left++;//反复右移left
        A[right] = A[left];//将A[left]挪到A[right]
    }
    A[left] = temp;//把temp放到left与right相遇的地方
    return left;//返回相遇的坐标
}

数学问题

简单数学

  • 在算法设计题目中，经常有一类题目与数学息息相关，这样的问题通常难度不大，也不需要特别的数学知识，只要掌握简单的梳理逻辑即可。
  • 下面来看一个例题：

例题：PAT B1019、PAT A1069

  • 思路：
  • 步骤 1：写出两个函数-> int 型整数转换成 int 型数组的 to_array() 函数（即把每一位都当成数组的一个元素）、int 型数组转换成 int 型整数的 to_number() 函数。
  • 步骤 2：建立一个 while 循环，对每一层循环：
  1. 用 to_array() 函数将 n 转换为数组并递增排序，再用 to_number() 函数将递增排序完的数组转换为整数 MIN。
  2. 将数组递减排序，再用 to_number() 函数将递减排序完的数组转换为整数 MAX。
  3. 令 n=MAX-MIN 为下一个数，并输出当前层的信息。
  4. 如果得到的 n 为 0 或 6174，退出循环。
  • 注意点：
  • 如果某步得到了不足 4 位的数，则视为在高位补 0，如 189 即为 0189。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
using namespace std;

//排序函数,从小到大
bool cmp_up(int a,int b)
{
    return a<b;
}

//排序函数,从大到小
bool cmp_down(int a,int b)
{
    return a>b;
}

//整数到数组
void to_array(int n,int num[])
{
    for(int i=0;i<4;i++)
    {
        num[i]=n%10;
        n=n/10;
    }
}

//数组到整数
int to_number(int num[])
{
    int ans=0;
    for(int i=0;i<4;i++)
    {
        ans=ans*10+num[i];
    }
    return ans;
}

//主函数
int main()
{
    //MIN和MAX分别表示递增排序和递减排序后得到的最小值和最大值
    int n,MIN,MAX;
    scanf("%d",&n);
    int num[5];
    while(1)
    {
        to_array(n,num);//将n转换为数组
        sort(num,num+4,cmp_up);
        MIN = to_number(num);
        sort(num,num+4,cmp_down);
        MAX = to_number(num);
        n = MAX - MIN;
        printf("%04d - %04d = %04d\n",MAX,MIN,n);
        if(n==0||n==6174)
            break;
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}

例题：西西弗斯串

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream> // 包含头文件<sstream>来使用std::ostringstream
using namespace std;

//处理函数
int solve(string str)
{
    int step=0,ou=0,ji=0,total=0;
    if(str=="123")
        return 0;
    else
    {
        while(1)
        {
            if(str=="123")
                break;
            else
            {
                for(int i=0;i<str.length();i++)
                {
                    if((str[i]-'0')%2==0)//偶数
                    {
                        ou++;
                        total++;
                    }
                    else
                    {
                        ji++;
                        total++;
                    }
                }
                str=to_string(ou)+to_string(ji)+to_string(total);
                ou=0,ji=0,total=0;
                step++;
            }
        }
        return step;
    }
}

//主函数
int main()
{
    string str;
    cin >> str;
    int ans;
    ans = solve(str);
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：
  • 这道题目主要使用了 to_string() 函数，需要包含 #include <sstream> 头文件，to_string() 是 C++11中的标准库函数，它将数字转换为字符串，并可以接受任何数字类型。

最大公约数与最小公倍数

最大公约数

  • 正整数 a 和 b 的最大公约数是指 a 与 b 的所有公约数中最大的那个公约数，例如 4 和 6 的最大公约数为 2，3 和 9 的最大公约数为 3。
  • 一般用 gcd(a,b) 来表示 a 和 b 的最大公约数，而求解最大公约数常用欧几里得算法（即辗转相除法）。
  • 欧几里得算法基于下面这个定理：
  • 设 a、b 均为正整数，则 gcd(a,b)=gcd(b,a%b):

证明：设 a=kb+ra=kb+r，其中 k 和 r 分别为 a 除以 b 得到的商和余数。
则有 r=a−kbr=a-kb 成立。
设 d 为 a 和 b 的一个公约数，
那么由 r=a−kbr=a-kb，得 d 也是 r 的一个约数。
因此 d 是 b 和 r 的一个公约数。
又由 r=a%b，得 d 为 b 和 a%b 的一个公约数。
因此 d 既是 a 和 b 的公约数，也是 b 和 a%b 的公约数。
由 d 的任意性，得 a 和 b 的公约数都是 b 和 a%b 的公约数。
由 a=kb+ra=kb+r 同理可证 b 和 a%b 的公约数都是 a 和 b 的公约数。
因此 a 和 b 的公约数与 b 和 a%b 的公约数全部相等，故其最大公约数也相等，
即有 gcd(a,b)=gcd(b,a%b)。
证毕！

  • 由上面定理可以发现：
  • 如果 a<b，那么定理的结果就是将 a 和 b 交换。
  • 如果 a>b，那么通过这个定理总可以将数据规模变小，并且减少得非常快。
  • 这样似乎可以很快得到结果，另外还需要一个东西：
  • 递归边界，即数据规模减少到什么程度使得可以算出结果来。
  • 显而易见，0 和任意一个整数 a 的最大公约数都是 a（注意：不是 0），此结论可以当作递归边界。
  • 因此很容易想到将其写成递归的形式，因为递归的两个关键已经得到：
  1. 递归式：gcd(a,b)=gcd(b,a%b)
  2. 递归边界：gcd(a,b)=a
  • 于是可以得到下面的求解最大公约数的代码：
1
2
3
4
5
6
7
int gcd(int a,int b)
{
	if(b==0)
		return a;
	else
		return gcd(b,a%b);
}
  • 更加简洁的写法是：
1
2
3
4
int gcd(int a,int b)
{
	return !b ? a : gcd(b,a%b);
}
  • 上面两段代码意义相同，可以自行选择。

例题：最大公约数

  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

//求解最大公约数函数(递归算法)
int gcd(int a,int b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}

//主函数
int main()
{
    int a,b,ans;
    scanf("%d %d",&a,&b);
    ans = gcd(a,b);
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：简单题，与上述最大公约数分析相同！

最小公倍数

  • 正整数 a 与 b 的最小公倍数是指 a 与 b 的所有公倍数中最小的那个公倍数，例如 4 和 6 的最小公倍数为 12，3 和 9 的最小公倍数是 9。
  • 一般用 lcm(a,b) 来表示 a 和 b 的最小公倍数。
  • 最小公倍数的求解在最大公约数的基础上进行，当得到 a 和 b 的最大公约数 d 之后，可以马上得到 a 和 b 的最小公倍数 a*b/d，这个公式通过集合可以很好地理解，如下图所示：

  • 由上图很容易发现，a 和 b 的最大公约数即集合 a 与集合 b 的交集，而最小公倍数为集合 a 和集合 b 的并集。
  • 要得到并集，由于 a*b 会使公因子部分多计算一次，因此需要除掉一次公因子，于是就得到了 a 与 b 的最小公倍数 a*b/d。
  • 由于 a*b 在实际计算时有可能溢出，因此更恰当的写法是 a/d*b。
  • 由于 d 是 a 和 b 的最大公约数，因此 a/d 一定可以整除。
  • 代码如下：
1
2
3
4
5
//最小公倍数求解函数
int lcm(int a,int b)
{
    return a/gcd(a,b)*b;
}

例题：最小公倍数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

//求解最大公约数函数(递归算法)
int gcd(int a,int b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}

//最小公倍数求解函数
int lcm(int a,int b)
{
    return a/gcd(a,b)*b;
}

//主函数
int main()
{
    int a,b,ans;
    scanf("%d %d",&a,&b);
    ans = lcm(a,b);
    printf("%d\n",ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：简单题，与上述最小公倍数分析相同！

分数的四则运算

  • 所谓分数的四则运算是指，给定两个分数的分子和分母，求它们加减乘除的结果。

分数的表示和化简

分数的表示
  • 对一个分数来说，最简洁的写法就是写成假分数的形式，即无论分子比分母大或者小，都保留其原数。因此可以使用一个结构体来存储这种只有分子和分母的分数：
1
2
3
4
struct Fraction //分数
{
	int up,down;//分子、分母
};
  • 于是就可以定义 Fraction 类型的变量来表示分数，或者定义数组来表示一堆分数。其中需要对这种表示制订三项规则：
  1. 使 down 为非负数。如果分数为负，那么令分子 up 为负即可。
  2. 如果该分数恰好为 0，那么规定其分子为 0，分母为 1。
  3. 分子和分母没有除了 1 以外的公约数。
分数的化简
  • 分数的化简主要用来使 Fraction 变量满足分数表示的三项规定，因此化简步骤也分为以下三步：
  1. 如果分母 down 为负数，那么令分子 up 和分母 down 都变为相反数。
  2. 如果分子 up 为 0，那么令分母 down 为 1。
  3. 约分：求出分子绝对值与分母绝对值的最大公约数 d,然后令分子分母同时除以 d。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//分数化简
Fraction reduction(Fraction result)
{
	if(result.down < 0)//分母为负数，令分子和分母都变为相反数
	{
		result.up = -result.up;
		result.down = -result.down;
	}
	if(result.up == 0)//如果分子为0
	{
		result.down = 1;//令分母为1
	}
	else//如果分子不为0，进行约分
	{
		int d = gcd(abs(result.up),abs(result.down));//分子分母的最大公约数
		result.up /= d;
		result.down /= d;
	}
	return result;
}

分数的四则运算

分数的加法
  • 对两个分数 f1 和 f2，其加法公式为：

result=f1.up×f2.down+f2.up×f1.downf1.down×f2.downresult=\frac{f1.up×f2.down+f2.up×f1.down}{f1.down×f2.down}

  • 代码如下：
1
2
3
4
5
6
7
8
//分数加法
Fraction add(Fraction f1,Fraction f2)//分数f1加分数f2
{
    Fraction result;
    result.up = f1.up*f2.down+f2.up*f1.down;//分数和的分子
    result.down = f1.down*f2.down;//分数和的分母
    return reduction(result);//返回化简后的结果分数
}
分数的减法
  • 对两个分数 f1 和 f2，其减法公式为：

result=f1.up×f2.down−f2.up×f1.downf1.down×f2.downresult=\frac{f1.up×f2.down-f2.up×f1.down}{f1.down×f2.down}

  • 代码如下：
1
2
3
4
5
6
7
8
//分数减法
Fraction minu(Fraction f1,Fraction f2)//分数f1减去分数f2
{
    Fraction result;
    result.up = f1.up*f2.down-f2.up*f1.down;//分数差的分子
    result.down = f1.down*f2.down;//分数差的分母
    return reduction(result);//返回化简后的结果分数
}
分数的乘法
  • 对两个分数 f1 和 f2，其乘法公式为：

result=f1.up×f2.upf1.down×f2.downresult=\frac{f1.up×f2.up}{f1.down×f2.down}

  • 代码如下：
1
2
3
4
5
6
7
8
//分数乘法
Fraction multi(Fraction f1,Fraction f2)//分数f1乘分数f2
{
    Fraction result;
    result.up = f1.up*f2.up;//分数积的分子
    result.down = f1.down*f2.down;//分数积的分母
    return reduction(result);//返回化简后的结果分数
}
分数的除法
  • 对两个分数 f1 和 f2，其除法公式为：

result=f1.up×f2.downf1.down×f2.upresult=\frac{f1.up×f2.down}{f1.down×f2.up}

  • 代码如下：
1
2
3
4
5
6
7
8
//分数除法
Fraction divide(Fraction f1,Fraction f2)//分数f1除分数f2
{
    Fraction result;
    result.up = f1.up*f2.down;//分数商的分子
    result.down = f1.down*f2.up;//分数商的分母
    return reduction(result);//返回化简后的结果分数
}
  • 除法有额外注意事项。如果读入的除数为 0（只需判断 f2.up 是否为 0），那么应当直接特别判断输出题目要求的输出语句（例如输出 Error、Inf 之类）。只有当除数不为 0 时候，才能用上面的函数进行计算。

分数的输出

  • 分数的输出根据题目的需要和要求进行，但是大体上有以下几个注意点：
  1. 输出分数前，需要先对其进行化简。
  2. 如果分数 r 的分母 down 为 1，说明该分数是整数，一般来说题目会要求直接输出分子，而省略分母的输出。
  3. 如果分数 r 的分子 up 的绝对值大于分母 down，说明该分数是假分数，此时应按带分数的形式输出，即整数部分为 r.upr.down\frac{r.up}{r.down}，分子部分为 abs(r.up)%r.down，分母部分为 r.down。
  4. 以上均不满足时说明分数 r 是真分数，按原样输出即可。
  • 以下是一个输出示例：
1
2
3
4
5
6
7
8
9
10
11
//分数输出
void showResult(Fraction r)//输出分数r
{
    r = reduction(r);
    if(r.down == 1)//输出整数
        printf("%d",r.up);
    else if(abs(r.up)>r.down)//输出假分数
        printf("%d %d/%d",r.up/r.down,abs(r.up)%r.down,r.down);
    else//输出真分数
        printf("%d/%d",r.up,r.down);
}
  • 强调：由于分数的乘法和除法的过程中可能使分子或者分母超过 int 型的表示范围，因此一般情况下，分子和分母应当使用 long long 型变量来存储。

素数

  • 素数又称为质数，是指除了 1 和本身之外，不能被其他数整除的一类数。
  • 即对给定的正整数 n，如果对任意的正整数 a (1<a<n)，都有 n%a!=0 成立，那么称 n 是素数；
  • 否则，如果存在 a (1<a<n)，使得 n%a==0，那么称 n 为合数。
  • 应特别注意的是，1 既不是素数，也不是合数。
  • 本节将解决两个问题：
  1. 如何判断给定的正整数 n 是否为质数；
  2. 如何在较短的时间内得到 1~n 内的素数表。

素数的判断

  • 从素数的定义可以知道，一个整数需要被判断为素数，需要判断 n 是否能被 2,3……,n-1 中的一个整除。
  • 只有 2,3……,n-1 都不能整除 n，n 才能判定为素数，而只要有一个能整除 n 的数出现，n 就可以判定为非素数。
  • 上述判定方法没有问题，复杂度为 O(n)O(n)，但在许多情况下，判定素数只是整个算法中的一部分，这时候 O(n)O(n) 的复杂度有点大，需要更加快速的判定方法。
  • 注意到如果在 2~n-1 中存在 n 的约数，不妨设为 k，即 n%k==0，那么由 k*(n/k)==n 可知，n/k 也是 n 的一个约数，且 k 与 n/k 中一定满足其中一个小于 sqrt(n) 、另一个大于 sqrt(n)，其中 sqrt(n) 为根号 n。
  • 这启发我们，只需要判定 n 能否被 2,3,……,⌊n⌋2,3,……,\lfloor{\sqrt{n}}\rfloor 中的一个整除（其中 ⌊x⌋\lfloor{x}\rfloor 表示对 x 向下取整），即可判定 n 是否为素数。该算法的复杂度为 O(n)O(\sqrt{n})。

  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
//判断是否为素数
bool isPrime(int n)
{
    if(n<=1)
        return false;//特判
    int sqr = (int)sqrt(1.0*n);//根号n
    for(int i=2;i<=sqr;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;
}
  • 在上述代码中，sqrt 的作用为一个浮点数取整，需要添加 #include <cmath>。由于 sqrt 的参数要求是浮点数，因此在 n 前面前面乘以 1.0 来使其成为浮点型。
  • 如果 n 没有接近 int 型变量的范围上界，那么可以有更为简单的写法：
1
2
3
4
5
6
7
8
9
10
11
12
//判断是否为素数
bool isPrime(int n)
{
    if(n<=1)
        return false;//特判
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;
}
  • 这样写会当 n 接近 int 型变量的范围上界时导致 i*i 溢出（当然 n 在 10910^9 以内都会是安全的），解决的办法是将 i 定义为 long long 型，这样就不会溢出了。
  • 但是更加推荐使用开根号的写法，会更加安全。

素数表的获取

  • 通过上面的学习，我们不难判断单独一个数是否为素数，那么可以直接由此得出打印 1~n 范围内的素数表的方法，即从 1~n 进行枚举，判断每个数是否为素数，如果是素数则加入素数表。
  • 这种方法枚举部分的复杂度是 O(n)O(n)，而判断素数的复杂度是 O(n)O(\sqrt{n})，因此，总复杂度是 O(nn)O(n\sqrt{n})。
  • 这个复杂度对 n 不超过 10510^5 的大小是没有问题的，大部分涉及素数表的题目都不会超过这个范围，代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
const int MAXN = 101;//表长
int prime[MAXN],pNum = 0;//prime数组存放所有素数，pNum为素数个数
bool p[MAXN] = {0};//p[i] == true表示i是素数
void Find_Prime()
{
	for(int i=1;i<MAXN;i++)
	{
		if(isPrime(i)==true)
		{
			prime[pNum++] = i;//是素数则把i存入prime数组
			p[i] = true;
		}
	}
}
  • 下面是完整的求解 100 以内的所有素数代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

const int MAXN = 101;//表长
int prime[MAXN],pNum = 0;//prime数组存放所有素数，pNum为素数个数
bool p[MAXN] = {0};//p[i] == true表示i是素数

//判断是否为素数
bool isPrime(int n)
{
    if(n<=1)
        return false;//特判
    int sqr = (int)sqrt(1.0*n);//根号n
    for(int i=2;i<=sqr;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;
}

//寻找素数表
void Find_Prime()
{
	for(int i=1;i<MAXN;i++)
	{
		if(isPrime(i)==true)
		{
			prime[pNum++] = i;//是素数则把i存入prime数组
			p[i] = true;
		}
	}
}

//主函数
int main()
{
    Find_Prime();
    for(int i=0;i<pNum;i++)
    {
        printf("%d ",prime[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
  • 上面的算法对于 n 在 10510^5 以内都是可以承受的，但是如果出现需要更大范围的素数表，O(nn)O(n\sqrt{n}) 的算法将力不从心。
  • 下面将介绍一种更加高效的算法，它的时间复杂度为 O(nloglogn)O(nloglogn)。
  • “筛法”是众多筛法中最简单且最容易理解的一种，即 Eratosthenes 筛法。更优的欧拉筛法可以达到 O(n)O(n) 的时间复杂度，此处不予赘述。
  • 素数筛法的关键就在一个“筛”字。算法从小到达枚举所有数，对每一个素数，筛去它的所有倍数，剩下的就是素数。
  • 下面看一个例子，求 1~15 中的所有素数：

① 2 是素数（唯一需要事先确定），因此筛去所有 2 的倍数，即 4、6、8、10、12、14。

2 3 4 5 6 7 6 9 10 11 12 13 14 15

② 3 没有被前面的步骤筛去,因此 3 是素数,筛去所有 3 的倍数,即 6、9、12、15。

2 3 4 5 6 7 8 9 10 11 12 13 14 15

③ 4 已经在①中被筛去，因此 4 不是素数。
④ 5 没有被前面的步骤筛去，因此 5 是素数，筛去所有 5 的倍数，即 10、15。

2 3 4 5 6 7 8 9 10 11 12 13 14 15

⑤ 6 已经在①中被筛去，因此 6 不是素数。
⑥ 7 没有被前面的步骤筛去，因此 7 是素数，筛去所有 7 的倍数，即 14。

2 3 4 5 6 7 8 9 10 11 12 13 14 15

⑦ 8 已经在①中被筛去，因此 8 不是素数。
⑧ 9 已经在②中被筛去，因此 9 不是素数。
⑨ 10 已经在①中被筛去，因此 10 不是素数。
⑩ 11 没有被前面的步骤筛去，因此 11 是素数，筛去所有 11 的倍数，但是 15 以内没有。
⑪ 12 已经在①中被筛去，因此 12 不是素数。
⑫ 13 没有被前面的步骤筛去，因此 13 是素数，筛去所有 13 的倍数，但是 15 以内没有。
⑬ 14 已经在⑥中被筛去，因此 14 不是素数。
⑭ 15 已经在②中被筛去，因此 15 不是素数。

  • 至此，1~15 内的所有素数已经全部得到，即 2、3、5、7、11、13。
  • 由上面的例子可以发现，当从小到大到达某数 a 时，如果 a 没有被前面步骤的数筛去，那么 a 一定是素数。
  • 这是因为，如果 a 不是素数，那么 a 一定有小于 a 的素因子，这样在之前的步骤中 a 一定会被筛掉，所以，如果当枚举到 a 时还没有被筛掉，那么 a 一定是素数。
  • 至于“筛”这个动作的实现，可以使用一个 bool 型数组 p 来标记。
  • 如果 a 被筛掉，那么 p[a]==true;。否则，p[a]==false;。
  • 在程序开始时可以初始化 p 数组全为 false。
  • 素数筛法的代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//寻找素数表(素数筛法)
void Find_Prime_2()
{
	for(int i=2;i<MAXN;i++)//从2开始，i<MAXN结束
	{
		if(p[i] == false)//如果i是素数
        {
            prime[pNum++] = i;//把素数i存到prime数组中
            for(int j=i+i;j<MAXN;j+=i)
            {
                //筛去所有i的倍数，循环条件不能写成j<=MAXN
                p[j] = true;
            }
        }
	}
}
  • 可以证明筛法的复杂度为 O(∑i=1nn/i)=O(nloglogn)O(\sum _{i=1}^{n}n/i)=O(nloglogn)。
  • 下面是两种方法函数完整求解 100 以内所有素数的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

const int MAXN = 101;//表长
int prime[MAXN],pNum = 0;//prime数组存放所有素数，pNum为素数个数
bool p[MAXN] = {false};//p[i] == true表示i是素数

//判断是否为素数
bool isPrime(int n)
{
    if(n<=1)
        return false;//特判
    int sqr = (int)sqrt(1.0*n);//根号n
    for(int i=2;i<=sqr;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;
}

//寻找素数表(普通法)
void Find_Prime()
{
	for(int i=1;i<MAXN;i++)
	{
		if(isPrime(i)==true)
		{
			prime[pNum++] = i;//是素数则把i存入prime数组
			p[i] = true;
		}
	}
}

//寻找素数表(素数筛法)
void Find_Prime_2()
{
	for(int i=2;i<MAXN;i++)//从2开始，i<MAXN结束
	{
		if(p[i] == false)//如果i是素数
        {
            prime[pNum++] = i;//把素数i存到prime数组中
            for(int j=i+i;j<MAXN;j+=i)
            {
                //筛去所有i的倍数，循环条件不能写成j<=MAXN
                p[j] = true;
            }
        }
	}
}

//主函数
int main()
{
    Find_Prime_2();
    for(int i=0;i<pNum;i++)
    {
        printf("%d ",prime[i]);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 输出：
1
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

例题：PAT B1013

  • 思路：把素数表打至第 N 个素数，然后按格式输出即可。
  • 注意点：
  1. 用筛法或者非筛法都可以解决问题，在算法只需要添加一句控制素数个数的语句：
1
2
if(num>=n)
	break;
  • 这是由于题目只要求输出第 m~n 个素数，因此超过 n 个素数之后的就不用保存了。
  1. 小技巧：由于空格在测试时肉眼看不出来，因此如果提交返回“格式错误”，可以把程序中的空格改成其他符号（比如 #）来输出，看看是哪里多了空格。
  2. 考虑到不知道第 10410^4 个素数有多大，不妨将测试上限 MAXN 设置得大一些，反正在素数个数超过 n 时会中断，不影响时间复杂度。当然也可以先用程序测试下第 10410^4 个素数是多少，然后再用这个数作为上限。
  3. 本题在素数表生成过程中其实可以直接输出，不过看起来会显得比较冗乱，因此还是应先生成完整素数表，然后再按格式要求输出。
  4. Find_Prime() 函数和 Find_Prime_2() 函数中要记得 i<MAXN 而不是 i<=MAXN，否则程序运行会崩溃。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

const int MAXN = 900000;//表长
int prime[MAXN],pNum = 0;//prime数组存放所有素数，pNum为素数个数
bool p[MAXN] = {false};//p[i] == true表示i是素数
int m,n;

//寻找素数表(素数筛法)
void Find_Prime_2()
{
	for(int i=2;i<MAXN;i++)//从2开始，i<MAXN结束
	{
		if(p[i] == false)//如果i是素数
        {
            prime[pNum++] = i;//把素数i存到prime数组中
            if(pNum>=n)
                break;
            else
            {
                for(int j=i+i;j<MAXN;j+=i)
                {
                    //筛去所有i的倍数，循环条件不能写成j<=MAXN
                    p[j] = true;
                }
            }
        }
	}
}

//主函数
int main()
{
    int num=0;
    scanf("%d %d",&m,&n);
    Find_Prime_2();
    for(int i=m-1;i<n;i++)
    {
        printf("%d",prime[i]);
        num++;
        if(num%10==0||i==n-1)
            printf("\n");
        else
            printf(" ");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：
  • 关于素数的题目有几个需要注意的点：
  1. 1 不是素数
  2. 素数表长至少要比 n 大 1。
  3. Find_Prime() 函数和 Find_Prime_2() 函数中要记得 i<MAXN 而不是 i<=MAXN，否则程序运行会崩溃。
  4. main() 函数中要记得调用 Find_Prime() 或 Find_Prime_2() 函数，不然不会得到结果。

质因子分解

  • 所谓质因子分解是指将一个正整数 n 写成一个或多个质数的乘积的形式，例如 6=2×36=2×3、8=2×2×28=2×2×2、180=2×2×3×3×5180=2×2×3×3×5。
  • 或者我们也可以写成指数的形式，例如 6=21×316=2^1×3^1、8=238=2^3、180=22×32×51180=2^2×3^2×5^1。
  • 显然，由于最后都要归结到若干不同质数的乘积，因此不妨先把素数表打印出来。而打印素数表的方法在上节已经阐述，下面我们主要就质因子分解本身进行讲解。
  • 注意：由于 1 本身不是素数，因此它没有质因子，下面的讲解是针对大于 1 的正整数来说的，而如果有些题目中要求对 1 进行处理，那么视题目条件而定来进行特判处理。
  • 由于每个质因子都可以不止出现一次，因此不妨定义结构体 factor，用来存放质因子及其个数，如下所示：
1
2
3
4
struct factor
{
	int x,cnt;//x为质因子，cnt为其个数
}fac[10];
  • 这里 fac[] 数组存放的就是给定的正整数 n 的所有质因子，例如对 180 来说，fac[] 数组如下：
1
2
3
4
5
6
7
8
fac[0].x = 2;
fac[0].cnt = 2;

fac[1].x = 3;
fac[1].cnt = 2;

fac[2].x = 5;
fac[2].cnt = 1;
  • 考虑到 2×3×5×7×11×13×17×19×23×292×3×5×7×11×13×17×19×23×29 就已经超过了 int 范围，因此对一个 int 型范围的数来说，fac[] 数组的大小只需要开到 10 就可以了。
  • 前面提到过，对一个正整数来说，如果它存在 1 和本身之外的因子，那么一定是在 n\sqrt{n} 的左右成对出现。
  • 而这里把这个结论用在“质因子”上面，会得到一个强化结论：
  • 对一个正整数 n 来说：
  • 如果它存在 [2,n] 范围内的质因子，要么这些质因子全部小于等于 n\sqrt{n}；
  • 要么只存在一个大于 n\sqrt{n} 的质因子，而其余质因子全部小于等于 n\sqrt{n}。
  • 这就给进行质因子分解提供了一个很好的思路：
  1. 枚举 1~ n\sqrt{n} 范围内的所有质因子 p，判断 p 是否为 n 的因子。
  • 如果 p 是 n 的因子，那么给 fac[] 数组增加质因子 p，并初始化其个数为 0。
  • 然后，只要 p 还是 n 的因子，就让 n 不断除以 p，每次操作令 p 的个数加 1，直到 p 不再是 n 的因子为止。
1
2
3
4
5
6
7
8
9
10
11
if(n%prime[i] == 0)//如果prime[i]是n的因子
{
	fac[num].x = prime[i];//记录该因子
	fac[num].cnt = 0;
	while(n%prime[i] == 0)//计算出质因子prime[i]的个数
	{
		fac[num].cnt++;
		n/=prime[i];
	}
	num++;//不同质因子个数加1
}
  • 如果 p 不是 n 的因子，就直接跳过。
  1. 如果在上面步骤结束后 n 仍然大于 1，说明 n 有且仅有一个大于 n\sqrt{n} 的质因子（有可能是 n 本身），这时需要把这个质因子加入 fac[] 数组中，并令其个数为 1。
1
2
3
4
5
if(n!=1)//如果无法被根号n以内的质因子除尽
{
	fac[num].x = n;//那么一定有一个大于根号n的质因子
	fac[num++].cnt = 1;
}
  • 至此，fac[] 数组中存放的就是质因子分解的结果，时间复杂度是 O(n)O(\sqrt{n})。

例题：PAT A1059

  • 题意：
  • 给出一个 int 范围的整数，按照从小到大的顺序输出其分解为质因数的乘法算式。
  • 思路：
  • 和上面讲解质因子分解的思路是完全相同的，要在前面先把素数表打印出来，然后再进行质因子分解的操作。
  • 注意点：
  • 题目说的 int 范围内的正整数进行质因子分解，因此素数表大概开 10510^5 大小就可以了。
  • 注意 n==1 的时候需要特判输出 1=1，否则不会输出结果。
  • 初学者学习素数和质因子分解比较容易犯的错误：
  1. 在 main() 函数开头忘记调用 Find_Prime() 函数或 Find_Prime_2() 函数；
  2. Find_Prime() 函数或 Find_Prime_2() 函数中把 i<MAXN 误写成 i<=MAXN；
  3. 没有处理好大于 n\sqrt{n} 部分的质因子；
  4. 在枚举质因子的过程中发生了死循环（死因各异）；
  5. 没有在循环外定义变量来存储 sqrt(n)，而在循环条件中直接计算 sqrt(n)，这样当循环中使用 n 本身进行操作的话会导致答案错误。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

struct factor
{
	int x,cnt;//x为质因子，cnt为其个数
} fac[10];

const int MAXN = 100010;//表长
int prime[MAXN],pNum = 0;//prime数组存放所有素数，pNum为素数个数
bool p[MAXN] = {false};//p[i] == true表示i是素数

//判断是否为素数
bool isPrime(int n)
{
    if(n<=1)
        return false;//特判
    int sqr = (int)sqrt(1.0*n);//根号n
    for(int i=2;i<=sqr;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;
}

//寻找素数表(普通法)
void Find_Prime()
{
	for(int i=1;i<MAXN;i++)
	{
		if(isPrime(i)==true)
		{
			prime[pNum++] = i;//是素数则把i存入prime数组
			p[i] = true;
		}
	}
}

//寻找素数表(素数筛法)
void Find_Prime_2()
{
	for(int i=2;i<MAXN;i++)//从2开始，i<MAXN结束
	{
		if(p[i] == false)//如果i是素数
        {
            prime[pNum++] = i;//把素数i存到prime数组中
            for(int j=i+i;j<MAXN;j+=i)
            {
                //筛去所有i的倍数，循环条件不能写成j<=MAXN
                p[j] = true;
            }
        }
	}
}

//主函数
int main()
{
    Find_Prime_2();
    int n,num=0;//num为n的不同质因子个数
    scanf("%d",&n);
    if(n==1)
        printf("1=1\n");//特判1的情况
    else
    {
        printf("%d=",n);
        int sqr = (int)sqrt(1.0*n);//n的根号
        //枚举根号n以内的质因子
        for(int i=0;i<pNum&&prime[i]<=sqr;i++)
        {
            if(n%prime[i] == 0)//如果prime[i]是n的因子
            {
	            fac[num].x = prime[i];//记录该因子
	            fac[num].cnt = 0;
	            while(n%prime[i] == 0)//计算出质因子prime[i]的个数
	            {
		            fac[num].cnt++;
		            n/=prime[i];
	            }
	            num++;//不同质因子个数加1
            }
            if(n==1)
                break;//及时退出循环，节省时间
        }
        if(n!=1)//如果无法被根号n以内的质因子除尽
        {
	        fac[num].x = n;//那么一定有一个大于根号n的质因子
	        fac[num++].cnt = 1;
        }
        for(int i=0;i<num;i++)
        {
            if(i>0)
                printf("*");
            printf("%d",fac[i].x);
            if(fac[i].cnt>1)
                printf("^%d",fac[i].cnt);
        }
        printf("\n");
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 最后指出，如果要求一个正整数 N 的因子个数，只需要对其质因子分解，得到各质因子 pip_i 的个数分别为 e1、e2、……、eke_1 、e_2 、…… 、e_k ，于是 N 的因子个数 d(n)d(n) 就是：

d(n)=(e1+1)×(e2+1)×...×(ek+1)d(n)=(e_1+1)\times(e_2+1)\times...\times(e_k+1)

  • 原因是，对每个质因子 pip_i 都可以选择其出现 00 次、11 次、…、eie_i 次，共 ei+1e_i+1 种可能，组合起来就是答案。
  • 而由同样的原理可知，N 的所有因子之和 s(n)s(n) 为：

\begin{equation} \begin{split} s(n) &= (1+p_1+p_1^2+...+p_1^{e_1})\times(1+p_2+p_1^2+...+p_2^{e_2})\times...\times(1+p_k+p_k^2+...+p_k^{e_k})\\ &=\frac{1-p_{1}^{e_{1}+1}}{1-p_{1}}\times\frac{1-p_{2}^{e_{2}+1}}{1-p_{2}}\times...\times\frac{1-p_{k}^{e_{k}+1}}{1-p_{k}} \end{split} \end{equation}

  • 上述因数个数定理与因数和定理的简单例子证明如下图所示：

例题：生成约数

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//主函数
int main()
{
    int n;
    set<int> ans;
    scanf("%d",&n);
    for(int i=1;i<=n/i;i++)
    {
        if(n%i==0)
        {
            ans.insert(i);
            ans.insert(n/i);
        }
    }
    set<int>::iterator it = ans.begin();
    for(set<int>::iterator it = ans.begin();it!=ans.end();it++)
    {
        if(it!=ans.begin())
        printf(" ");
        printf("%d",*it);
    }
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：
  • 约数一定是成双出现的，如果一个约数是 i，那么另一个约数就必然是 n/i，我们枚举较小的那一个，也就是满足 i<=n/i 的约数，另外一个我们直接用 n/i 计算算出来即可。
  • 上述方法称为式除法，该方法的时间复杂度为 O(n)O(\sqrt{n}) ，其核心代码如下：
1
2
3
4
5
6
7
8
9
10
11
int n;
set<int> ans;
scanf("%d",&n);
for(int i=1;i<=n/i;i++)
{
    if(n%i==0)
    {
        ans.insert(i);
        ans.insert(n/i);
    }
}

大整数运算

  • 对于一道 A+B 的题目，如果 A 和 B 的范围在 int 范围内，那么相对比较简单。
  • 但是如果 A 和 B 是有着 1000 个数位的整数，将没有办法用已有的数据类型来表示，这时就只能去模拟加减乘除的过程。
  • 大整数又称为高精度整数，其含义就是用基本数据类型无法存储其精度的整数。

大整数的存储

  • 对于大整数的存储，一般使用数组即可。
  • 例如定义 int 型数组 d[1000]，那么这个数组中的每一位就代表了存放的整数的每一位。
  • 如将 235813 存储到数组中，则有 d[0]=3、d[1]=1、d[2]=8、d[3]=5、d[4]=3、d[5]=2，即整数的高位存储在数组的高位，整数的低位存储在数组的低位。
  • 不反过来存储的原因是，在进行运算的时候都是从整数的低位到高位进行枚举，顺位存储和这种思维相合。
  • 但也会由此产生一个需要注意的问题：
  • 把整数按字符串 %s 读入的时候，实际上是逆位存储的，即 str[0]='2'、str[1]='3'、…、 str[5]='3'，因此在读入之后需要在另存为至 d[] 数组的时候反转一下。
  • 而为了方便随时获取大整数的长度，一般都会定义一个 int 型变量 len 来记录其长度，并和 d 数组组合成结构体：
1
2
3
4
5
struct bign
{
	int d[1000];
	int len;
};
  • 上述 bign 是 big number 的缩写。
  • 显然，在定义结构体变量之后，需要马上初始化结构体。为了减少在实际输入代码的过程中总是忘记初始化的问题，最好使用以前介绍的“构造函数”，即在结构体内部加入以下代码：
1
2
3
4
5
bign()
{
	memset(d,0,sizeof(d));
	len = 0;
}
  • "构造函数"是用来初始化结构体的函数，函数名和结构体名相同、无返回值，因此非常好写。
  • 因此大整数结构体 bign 就变成了这样：
1
2
3
4
5
6
7
8
9
10
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};
  • 这样在每次定义结构体变量时，都会自动对该变量进行初始化。
  • 而在输入大整数时，一般都是先用字符串读入，然后再把字符串另存至 bign 结构体中。由于使用 char 数组进行读入时，整数的高位会变成数组的低位，而整数的低位会变成数组的高位，因此为了让整数在 bign 中是顺位存储的，需要让字符串倒着赋给 d[] 数组：
1
2
3
4
5
6
7
8
9
10
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}
  • 如果要比较 bign 变量的大小，规则也很简单：
  • 先判断两者 len 的大小，如果不相等，则以长的为大；如果相等，则从高位到低位进行比较，直到出现某一位不等，就可以判断两个数大小，上述规则的代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int compare(bign a,bign b)//比较a和b的大小，a大，相等，a小分别返回1、0、-1
{
	if(a.len>b.len)
		return 1;//a大
	else if(a.len<b.len)
		return -1;//a小
	else
	{
		for(int i=a.len-1;i>=0;i--)//从高位往低位比较
		{
			if(a.d[i]>b.d[i])
				return 1;//只要有一位a大，则a大
			else if(a.d[i]<b.d[i])
				return -1;//只要有一位a小，则a小
		}
		return 0;//两数相等
	}
}

例题：大整数比较

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//比较函数
int compare(bign a,bign b)//比较a和b的大小，a大，相等，a小分别返回1、0、-1
{
	if(a.len>b.len)
		return 1;//a大
	else if(a.len<b.len)
		return -1;//a小
	else
	{
		for(int i=a.len-1;i>=0;i--)//从高位往低位比较
		{
			if(a.d[i]>b.d[i])
				return 1;//只要有一位a大，则a大
			else if(a.d[i]<b.d[i])
				return -1;//只要有一位a小，则a小
		}
		return 0;//两数相等
	}
}

//主函数
int main()
{
    char str1[1000],str2[1000];
    int num;
    scanf("%s%s",str1,str2);
    bign a = change(str1);
    bign b = change(str2);
    num = compare(a,b);
    if(num==1)
        printf("a > b");
    else if(num==-1)
        printf("a < b");
    else
        printf("a = b");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。
  • 接下来主要介绍四个运算：
  1. 高精度加法
  2. 高精度减法
  3. 高精度与低精度乘法
  4. 高精度与低精度除法
  • 至于高精度与高精度的乘法和除法，有兴趣自行了解。

大整数的四则运算

高精度加法
  • 以 147+65 为例：

  1. 7+5=12，取个位数 2 作为该位的结果，取十位数 1 进位。
  2. 4+6 加上进位 1 为 11，取个位数 1 作为该位的结果，取十位数 1 进位。
  3. 1+0，加上进位 1 为 2，取个位数 2 作为该位的结果，由于十位数为 0，因此不进位。
  • 可以因此归纳出对其中一位进行加法的步骤：
  • 将该位上的两个数字和进位相加，得到的结果取个位数作为该位结果，取十位数作为新的进位。
  • 高精度加法的做法与此完全相同，实现代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
bign add(bign a,bign b)//高精度a+b
{
	bign c;
	int carry = 0;//carry是进位
	for(int i=0;i<a.len||i<b.len;i++)//以较长的为界限
	{
		int temp = a.d[i]+b.d[i]+carry;//两个对应位与进位相加
		c.d[c.len++]=temp % 10;//个位数为该位结果
		carry = temp / 10;//十位是新的进位
	}
	if(carry!=0)//如果最后进位不为0，则直接赋给结果的最高位
		c.d[c.len++] = carry;
	return c;
}
  • 高精度相加的代码大概只有十行，非常简洁，只要懂得原理，基本上可以很容易理解和记住。

例题：大整数加法

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//比较函数
int compare(bign a,bign b)//比较a和b的大小，a大，相等，a小分别返回1、0、-1
{
	if(a.len>b.len)
		return 1;//a大
	else if(a.len<b.len)
		return -1;//a小
	else
	{
		for(int i=a.len-1;i>=0;i--)//从高位往低位比较
		{
			if(a.d[i]>b.d[i])
				return 1;//只要有一位a大，则a大
			else if(a.d[i]<b.d[i])
				return -1;//只要有一位a小，则a小
		}
		return 0;//两数相等
	}
}

//高精度a+b
bign add(bign a,bign b)//高精度a+b
{
	bign c;
	int carry = 0;//carry是进位
	for(int i=0;i<a.len||i<b.len;i++)//以较长的为界限
	{
		int temp = a.d[i]+b.d[i]+carry;//两个对应位与进位相加
		c.d[c.len++]=temp % 10;//个位数为该位结果
		carry = temp / 10;//十位是新的进位
	}
	if(carry!=0)//如果最后进位不为0，则直接赋给结果的最高位
		c.d[c.len++] = carry;
	return c;
}

//主函数
int main()
{
    char str1[1000],str2[1000];
    int num;
    scanf("%s%s",str1,str2);
    bign a = change(str1);
    bign b = change(str2);
    bign c = add(a,b);
    for(int i=c.len-1;i>=0;i--)
        printf("%d",c.d[i]);
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。
高精度减法
  • 以 147-65 为例：

  1. 5-7<0，不够减，因此从高位 4 借 1，于是 4 减 1 变成 3，该位结果为 15-7=8；
  2. 3-6<0，不够减，因此从高位 1 借 1，于是 1 减 1 变成 0，该位结果为 13-6=7；
  3. 上面和下面均为 0，结束计算。
  • 同样可以得到一个很简练的步骤：
  • 对某一步，比较被减位和减位，如果不够减，则令被减位的高位减 1、被减位加 10 再进行减法；
  • 如果够减，则直接减。
  • 最后一步要注意减法后高位可能有多余的 0，要忽视它们，但也要保证结果至少有一位数。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bign sub(bign a,bign b)//高精度a-b
{
	bign c;
	for(int i=0;i<a.len||i<b.len;i++)//以较长的为界限
	{
		if(a.d[i]<b.d[i])//如果不够减
		{
			a.d[i+1]--;//向高位借位
			a.d[i]+=10;//当前位加10
		}
		c.d[c.len++] = a.d[i]-b.d[i];//减法结果为当前位结果
	}
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;
	}
	return c;
}
  • 需要指出的是，使用 sub() 函数前要比较两个数的大小，如果被减数小于减数，需要交换两个变量，然后输出负号，再使用 sub() 函数。

例题：大整数减法

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//比较函数
int compare(bign a,bign b)//比较a和b的大小，a大，相等，a小分别返回1、0、-1
{
	if(a.len>b.len)
		return 1;//a大
	else if(a.len<b.len)
		return -1;//a小
	else
	{
		for(int i=a.len-1;i>=0;i--)//从高位往低位比较
		{
			if(a.d[i]>b.d[i])
				return 1;//只要有一位a大，则a大
			else if(a.d[i]<b.d[i])
				return -1;//只要有一位a小，则a小
		}
		return 0;//两数相等
	}
}

//高精度a-b
bign sub(bign a,bign b)//高精度a-b
{
	bign c;
	for(int i=0;i<a.len||i<b.len;i++)//以较长的为界限
	{
		if(a.d[i]<b.d[i])//如果不够减
		{
			a.d[i+1]--;//向高位借位
			a.d[i]+=10;//当前位加10
		}
		c.d[c.len++] = a.d[i]-b.d[i];//减法结果为当前位结果
	}
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;
	}
	return c;
}

//主函数
int main()
{
    char str1[1000],str2[1000];
    int num;
    scanf("%s%s",str1,str2);
    bign a = change(str1);
    bign b = change(str2);
    num = compare(a,b);
    if(num==-1)//a比b小
    {
        bign temp = a;
        a = b;
        b = temp;
        printf("-");
    }
    bign c = sub(a,b);
    for(int i=c.len-1;i>=0;i--)
        printf("%d",c.d[i]);
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。
高精度与低精度乘法
  • 所谓的低精度就是可以用基本数据类型存储的数据，例如 int 型。
  • 以 147×35 为例，这里把 147 视为高精度 bign 型，而 35 视为 int 类型，并且在下面的过程中，始终将 35 作为一个整体看待。

  1. 7×35=245，取个位数 5 作为该位结果，高位部分 24 作为进位。
  2. 4×35=140，加上进位 24，得 164，取个位数 4 为该位结果，高位部分 16 作为进位。
  3. 1×35=35，加上进位 16，得 51，取个位数 1 为该位结果，高位部分 5 作为进位。
  4. 接下来没有数相乘了，此时进位还不为 0，就把进位 5 直接作为结果的高位。
  • 对于某一步而言是这么一个步骤：
  • 取 bign 的某位与 int 型整体相乘，再与进位相加，所得结果的个位数作为该位结果，高位部分作为新的进位。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bign multi(bign a,int b)//高精度与低精度乘法
{
	bign c;
	int carry = 0;//进位
	for(int i=0;i<a.len;i++)
	{
		int temp = a.d[i] * b + carry;
		c.d[c.len++] = temp % 10;//个位作为该位结果
		carry = temp / 10;//高位部分作为新的进位
	}
	while(carry!=0)//和加法不一样，乘法的进位可能不止一位
	{
		c.d[c.len++] = carry % 10;
		carry /= 10;
	}
	return c;
}
  • 完整的 A×B 的代码只需要把高精度加法里的 add() 函数改成这里的 multi() 函数，并注意输入的时候 b 是作为 int 型输入即可。
  • 另外，如果 a 和 b 中存在负数，需要先记录下其负号，然后取它们的绝对值代入函数。

例题：大整数乘法I

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//高精度与低精度乘法
bign multi(bign a,int b)
{
	bign c;
	int carry = 0;//进位
	for(int i=0;i<a.len;i++)
	{
		int temp = a.d[i] * b + carry;
		c.d[c.len++] = temp % 10;//个位作为该位结果
		carry = temp / 10;//高位部分作为新的进位
	}
	while(carry!=0)//和加法不一样，乘法的进位可能不止一位
	{
		c.d[c.len++] = carry % 10;
        carry /= 10;
	}
	return c;
}

//主函数
int main()
{
    char str1[1000];
    int num,b;
    scanf("%s %d",str1,&b);
    bign a = change(str1);
    if(b==0)
        printf("0");
    else
    {
        bign c = multi(a,b);
        for(int i=c.len-1;i>=0;i--)
            printf("%d",c.d[i]);
    }
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。
高精度与低精度除法
  • 除法的计算以 1234/7 为例：

  1. 1 与 7 比较，不够除，因此该位商为 0，余数为 1。
  2. 余数 1 与新位 2 组合成 12，12 与 7 比较，够除，商为 1，余数为 5。
  3. 余数 5 与新位 3 组合成 53，53 与 7 比较，够除，商为 7，余数为 4。
  4. 余数 4 与新位 4 组合成 44，44 与 7 比较，够除，商为 6，余数为 2。
  • 归纳其中某一步的步骤：
  • 上一步的余数乘以 10 加上该步的位，得到该步临时的被除数，将其与除数比较：
  • 如果不够除，则该位的商为 0；
  • 如果够除，则商即为对应的商，余数即为对应的余数。
  • 最后一步要注意减法后高位可能有多余的 0，要忽视它们，但也要保证结果至少有一位数。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bign divide(bign a,int b,int& r)//高精度除法，r为余数
{
	bign c;
	//被除数的每一位和商的每一位是一一对应的，因此先令长度相等
	c.len = a.len;
	for(int i = a.len-1;i>=0;i--)//从高位开始
	{
		r = r * 10 + a.d[i];//和上一位遗留的余数组合
		if(r<b)
			c.d[i] = 0;//不够除，该位为0
		else//够除
		{
			c.d[i] = r / b;//商
			r = r % b;//获得新的余数
		}
	}
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;//去除高位的0.同时至少保留一位最低位
	}
	return c;
}
  • 在上述代码中，考虑到函数每次只能返回一个数据，而很多题目里面会经常要求得到余数。
  • 因此把余数写成“引用”的形式直接作为参数传入，或是把 r 设成全局变量。
  • 引用的作用是在函数中可以视作直接对原变量进行修改，而不像普通函数参数那样，在函数中的修改不影响原变量的值。这样当函数结束时，r 的值就是最终的余数。

例题：大整数除法

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[1000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//高精度除法，r为余数
bign divide(bign a,int b,int& r)
{
	bign c;
	//被除数的每一位和商的每一位是一一对应的，因此先令长度相等
	c.len = a.len;
	for(int i = a.len-1;i>=0;i--)//从高位开始
	{
		r = r * 10 + a.d[i];//和上一位遗留的余数组合
		if(r<b)
			c.d[i] = 0;//不够除，该位为0
		else//够除
		{
			c.d[i] = r / b;//商
			r = r % b;//获得新的余数
		}
	}
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;//去除高位的0.同时至少保留一位最低位
	}
	return c;
}

//主函数
int main()
{
    char str1[1000];
    int num,b,r;
    scanf("%s %d",str1,&b);
    bign a = change(str1);
    if(b==0)
        printf("undefined");
    else
    {
        bign c = divide(a,b,r);
        for(int i=c.len-1;i>=0;i--)
            printf("%d",c.d[i]);
        printf(" %d",r);
    }
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。
高精度与高精度乘法
  • 乘法的基本步骤模拟如下图：

  • 不难发现，上述步骤有以下关系：

\begin{equation} \begin{split} & c_0=a_0 \times b_0 \\ & c_1=a_1 \times b_0 + a_0 \times b_1 + carry \\ & c_2=a_2 \times b_0 + a_1 \times b_1 + carry \\ & c_3=a_2 \times b_1 + carry \end{split} \end{equation}

  • 因此模拟乘法的过程如下：
  • 用其中一个数的每一位 a.d[i]（从低位开始）逐位与另一个数的每一位 b.d[j] 相乘，结果存储在 c.d[i+j] 位，并处理进位。
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//高精度与高精度乘法
bign multi_high(bign a,bign b)
{
	bign c;
	int carry = 0;//进位
    int w;
    for(int i=0;i<a.len;i++)
    {
        for(int j=0;j<b.len;j++)
        {
            w=i+j;
            c.d[w] = c.d[w] + a.d[i]*b.d[j];
            carry = c.d[w] / 10;
            c.d[w+1] = c.d[w+1] + carry;
            c.d[w] %= 10;
        }
    }
    c.len = w+2;
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;//去除高位的0.同时至少保留一位最低位
	}
	return c;
}

例题：大整数乘法II

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
#include <set>
using namespace std;

//结构体
struct bign
{
	int d[10000];
	int len;
	bign()
	{
		memset(d,0,sizeof(d));
		len = 0;
	}
};

//整数转换为bign函数
bign change(char str[])//将整数转换为bign
{
	bign a;
	a.len = strlen(str);//bign的长度就是字符串长度
	for(int i=0;i<a.len;i++)
	{
		a.d[i]=str[a.len-i-1]-'0';//逆着赋值
	}
	return a;
}

//高精度与高精度乘法
bign multi_high(bign a,bign b)
{
	bign c;
	int carry = 0;//进位
    int w;
    for(int i=0;i<a.len;i++)
    {
        for(int j=0;j<b.len;j++)
        {
            w=i+j;
            c.d[w] = c.d[w] + a.d[i]*b.d[j];
            carry = c.d[w] / 10;
            c.d[w+1] = c.d[w+1] + carry;
            c.d[w] %= 10;
        }
    }
    c.len = w+2;
	while(c.len-1>=1&&c.d[c.len-1]==0)
	{
		c.len--;//去除高位的0.同时至少保留一位最低位
	}
	return c;
}

//主函数
int main()
{
    char str1[1000],str2[1000];
    int num;
    scanf("%s%s",str1,str2);
    bign a = change(str1);
    bign b = change(str2);
    bign c = multi_high(a,b);
    for(int i=c.len-1;i>=0;i--)
        printf("%d",c.d[i]);
    printf("\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。

扩展欧几里得算法

  • 本节主要分为 4 个部分：
  1. 扩展欧几里得算法（即 ax+by=gcd(a,b) 的求解）
  2. 方程 ax+by=c 的求解
  3. 同余式 ax=c(mod m) 的求解
  4. 逆元的求解以及 (b/a)%m 的计算。
  • 本节数学证明较多，需要认真领会。

扩展欧几里得算法

  • 扩展欧几里得算法用来解决这样一个问题：
  • 给定两个非零整数 a 和 b ，求一组整数解 (x,y)，使得 ax+by=gcd(a,b)，其中 gcd(a,b) 表示 a 和 b 的最大公约数。
  • 通过相关定理可知解一定存在，为了讨论问题方便，记 gcd=gcd(a,b)，其中 a 和 b 为初始给定的数值，因此可以认为在下面讨论的过程中 gcd 是一个固定的数。
  • 通过回忆之前介绍的欧几里得算法，如下代码所示：
1
2
3
4
5
6
7
int gcd(int a,int b)
{
	if(b==0)
		return a;
	else
		return gcd(b,a%b);
}
  • 它总是把 gcd(a,b) 转化为求解 gcd(b,a%b)，而当 b 变为 0 时返回 a，此时的 a 就等于 gcd。
  • 也就是说，欧几里得算法结束的时候变量 a 中存放的是 gcd，变量 b 中存放的是 0,因此此时显然有 a*1+b*0=gcd 成立，此时有 x=1、y=0 成立。
  • 不妨利用上面欧几里得算法的过程来计算 x 和 y。目前已知的是递归边界成立时为 x=1、y=0，需要想办法反推出最初始的 x 和 y。
  • 当计算 gcd(a,b) 时，有 ax1+by1=gcdax_1+by_1=gcd 成立；
  • 而在下一步计算 gcd(b,a%b) 时，又有 bx2+(a%b)y2=gcdbx_2+(a\%b)y_2=gcd 成立。
  • 又考虑到有关系 a%b=a−(a/b)∗ba\%b=a-(a/b)*b 成立（此处除法为整除）；
  • 因此 ax1+by1=bx2+(a−(a/b)∗b)y2ax_1+by_1=bx_2+(a-(a/b)*b)y_2 成立（此处除法为整除）；
  • 整理等号右边式子得：ax1+by1=ay2+b(x2−(a/b)y2)ax_1+by_1=ay_2+b(x_2-(a/b)y_2)。
  • 对比等号左右两边可以马上得到下面的递推公式：

{x1=y2y1=x2−(a/b)y2\left \{\begin{array} {l}x_{1}=y_{2} \\ y_{1}=x_{2}-(a/b)y_{2} \end{array} \right.

  • 由此便可以通过 x2x_2 和 y2y_2 来反推出 x1x_1 和 y1y_1 了，只需要在达到递归边界、不断退出的过程中根据上面的公式计算 x 和 y，就可以得到一组解。代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int exGcd(int a,int b,int &x,int &y)//x和y使用引用
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	int g = exGcd(b,a%b,x,y);//递归计算exGcd(b,a%b,x,y)
	int temp = x;//存放x的值
	x=y;//更新x=y(old)
	y=temp-a/b*y;//更新y=x(old)-a/b*y(old)
	return g;//g是gcd
}
  • 由于使用了引用，因此当 exGcd() 函数结束时 x 和 y 就是所求的解。
  • 显然，在得到这样一组解之后，就可以通过下面的式子得到全部解：

  • 下面来简单证明：
  • 假设新的解为 x+s1x+s_1 、y−s2y-s_2，即有 a∗(x+s1)+b∗(y−s2)=gcda*(x+s_1)+b*(y-s_2)=gcd 成立，通过代入 ax+by=gcdax+by=gcd 可以得到 as1=bs2as_1=bs_2，于是 s1s2=ba\frac{s_{1}}{s_{2}}=\frac{b}{a} 成立。
  • 为了让 s1s_1 和 s2s_2 尽可能小，可以让分子和分母同时除以一个尽可能大的数，同时保证它们仍然是整数。
  • 显然，由于 bgcd\frac{b}{gcd} 与 agcd\frac{a}{gcd} 互质，因此 gcd 是允许作为除数的最大数 s1s2=ba=bgcdagcd\frac{s_{1}}{s_{2}}=\frac{b}{a}=\frac{\frac{b}{gcd}}{\frac{a}{gcd}}，得 s1s_1 和 s2s_2 的最小取值是 bgcd\frac{b}{gcd} 与 agcd\frac{a}{gcd}，证毕！
  • 也就是说，x 和 y 的所有解分别以 bgcd\frac{b}{gcd} 与 agcd\frac{a}{gcd} 为周期。
  • 那么其中 x 的最小非负整数解是什么呢？
  • 从直观上来看就是 x%bgcdx\%\frac{b}{gcd}。
  • 但是由于通过 exGcd() 函数计算出来的 x、y 可正可负，因此实际上 x%bgcdx\%\frac{b}{gcd} 会得到一个负数，例如 (-15)%4=-3。
  • 考虑到即便 x 是负数，x%bgcdx\%\frac{b}{gcd} 的范围也是在 (−x%bgcd,0)(-x\%\frac{b}{gcd},0)，因此对任意整数而言，(x%bgcd+bgcd)%bgcd(x\%\frac{b}{gcd}+\frac{b}{gcd})\%\frac{b}{gcd} 才是对应的最小非负整数解。
  • 特殊的，如果 gcd==1，全部解的公式简化为下式，且 x 的最小非负整数解也可以简化为 (x%b+b)%b(x\%b+b)\%b。全部解为：


例题：二元一次方程的整数解

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

//求解最大公约数函数(递归算法)
int gcd(int a,int b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}

//扩展欧几里得算法
int exGcd(int a,int b,int &x,int &y)//x和y使用引用
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	int g = exGcd(b,a%b,x,y);//递归计算exGcd(b,a%b,x,y)
	int temp = x;//存放x的值
	x=y;//更新x=y(old)
	y=temp-a/b*y;//更新y=x(old)-a/b*y(old)
	return g;//g是gcd
}

//主函数
int main()
{
    int a,b;
    scanf("%d %d",&a,&b);
    int x,y,g;
    g=exGcd(a,b,x,y);
    int x_ans,y_ans;
    x_ans=(x%(b/g)+b/g)%(b/g);
    y_ans=(g-a*x_ans)/b;
    printf("%d %d\n",x_ans,y_ans);
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：该题目与上述介绍的思路一致，属于简单题。

方程 ax+by=c 的求解

  • 至此我们已经知道如何求解 ax+by=gcd 的解，其最常见的应用就是用来求解 ax+by=c，其中 c 为任意整数。
  • 首先，假设 ax+by=gcd 有一组解 (x0,y0)(x_0,y_0)，现在在其等号两边同时乘 cgcd\frac{c}{gcd}，即有 acx0gcd+bcy0gcd=ca\frac{cx_0}{gcd}+b\frac{cy_0}{gcd}=c 成立，因此 (x,y)=(cx0gcd,cy0gcd)(x,y)=(\frac{cx_0}{gcd},\frac{cy_0}{gcd}) 是 ax+by=c 的一组解。
  • 但是显然这样做的充要条件是 c%gcd==0，否则第一步在等号两边同时乘 cgcd\frac{c}{gcd} 都无法做到。
  • 于是 ax+by=c 存在解的充要条件是 c%gcd==0，且一组解 (x,y)=(cx0gcd,cy0gcd)(x,y)=(\frac{cx_0}{gcd},\frac{cy_0}{gcd}) 。
  • 为了获得全部解的公式，可以模仿之前的做法，假设新的解为 x+s1x+s_1 、y−s2y-s_2，然后将 a(x+s1)+b(y−s2)=ca(x+s_1)+b(y-s_2)=c 与 ax+by=cax+by=c 联立，发现同样可以得到 s1s2=ba\frac{s_{1}}{s_{2}}=\frac{b}{a} 成立。
  • 于是因为同样的原因，s1s_1 和 s2s_2 的最小值仍然是 bgcd\frac{b}{gcd} 与 agcd\frac{a}{gcd}。因此 ax+by=cax+by=c 的全部解的公式为：

  • 由此会发现与 ax+by=gcdax+by=gcd 全部解的公式是一样的，唯一不同的是初始解 (x,y)(x,y) 不同。
  • 因此对 ax+by=cax+by=c 来说，其解 (x,y)(x,y) 同样分别以 bgcd\frac{b}{gcd} 与 agcd\frac{a}{gcd} 为周期。
  • 除此之外，可以得到和上面一样的结论，对任意整数来说，(x%bgcd+bgcd)%bgcd(x\%\frac{b}{gcd}+\frac{b}{gcd})\%\frac{b}{gcd} 是 ax+by=cax+by=c 中 xx 的最小非负整数，一般来说可以让 xx 取 cx0gcd\frac{cx_0}{gcd}，其中 x0x_0 是 ax+by=gcdax+by=gcd 的一个解。
  • 并且，如果 gcd==1，那么全部解的公式可以化简为下式，且 xx 的最小非负整数解可以简化为 (x%b+b)%b(x\%b+b)\%b。全部解为：


例题：二元一次方程的整数解II

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

//求解最大公约数函数(递归算法)
int gcd(int a,int b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}

//扩展欧几里得算法
int exGcd(int a,int b,int &x,int &y)//x和y使用引用
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	int g = exGcd(b,a%b,x,y);//递归计算exGcd(b,a%b,x,y)
	int temp = x;//存放x的值
	x=y;//更新x=y(old)
	y=temp-a/b*y;//更新y=x(old)-a/b*y(old)
	return g;//g是gcd
}

//主函数
int main()
{
    int a,b,c;
    scanf("%d %d %d",&a,&b,&c);
    if(c%gcd(a,b)!=0)
        printf("No Solution\n");
    else
    {
        int x,y,g;
        g=exGcd(a,b,x,y);
        int x_ans,y_ans;
        //分b/g的正负
        if(b/g<0)
            x_ans=((x*c/g)%(b/g)-b/g)%(b/g);
        else
            x_ans=((x*c/g)%(b/g)+b/g)%(b/g);
        y_ans=(c-a*x_ans)/b;
        printf("%d %d\n",x_ans,y_ans);
    }
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目需要注意 b/g 是否为负数，其余部分上述介绍的思路一致，属于简单题。

同余式 ax=c(mod m)的求解

  • 既然已经解决了 ax+by=cax+by=c 的求解问题, 不得不提及同余式 ax≡c(mod m)ax\equiv c(mod \ m) 的求解。
  • 先解释什么是同余式：
  • 对整数 a、b、m 来说，如果 m 整除 a-b（即 (a-b)%m=0），那么就说 a 与 b 模 m 同余，对应的同余式为 a≡b(mod m)a\equiv b(mod \ m)，m 称为同余式的模。
  • 例如 10 与 13 模 3 同余，10 也与 1 模 3 同余，它们分别记为 10≡13(mod 3)10\equiv 13(mod \ 3)、10≡1(mod 3)10\equiv 1(mod \ 3)。
  • 显然，每一个整数都各自与 [0,m) 中的唯一的整数同余。
  • 此处要解决的就是同余式 ax≡c(mod m)ax\equiv c(mod \ m) 的求解。
  • 根据同余式的定义，有 (ax−c)%m=0(ax-c)\% m=0 成立，因此存在整数 y，使得 ax-c=my 成立，移项并令 y=-y 后即得 ax+my=c。
  • 由上节结论，当 c%gcd(a,m)==0 时方程才有解，且解的形式如下，其中 (x,y) 是 ax+my=c 的一组解，可以先通过求解 ax+my=gcd(a,m) 得到 (x0,y0)(x_0,y_0)，然后由公式 (x,y)=(cx0gcd(a,m),cy0gcd(a,m))(x,y)=(\frac{cx_0}{gcd(a,m)},\frac{cy_0}{gcd(a,m)}) 直接得到。

  • 虽然对方程 ax+my=c 来说，K 可以取任意整数，但是对同余式来说会有很多解在模 m 意义下是相同的（由于只关心 x，因此下面只考虑 x）。
  • 对同余式来说，只需要找出那些在模 m 意义下不同的解。
  • 因此考虑 x′=x+mgcd(a,m)∗Kx^{ \prime } =x+\frac { m }{ gcd(a,m )}*K，会发现当 K 分别取 0、1、2、…、gcd(a,m)-1 时，所得到的解在模 m 意义下是不同的，而其他解都可以对应到 K 取这 gcd(a,m) 个数值之一。
  • 由此可以得到结论：
  • 设 a, c, m 是整数，其中 m≥1，则
  1. 若 c%gcd(a,m)!=0，则同余式方程 ax≡c(mod m)ax\equiv c(mod \ m) 无解；
  2. 若 c%gcd(a,m)==0，则同余式方程 ax≡c(mod m)ax\equiv c(mod \ m) 恰好有 gcd(a,m) 个模 m 意义下不同的解，且解的形式为：

x′=x+mgcd(a,m)∗Kx^{\prime}=x+\frac{m}{gcd(a,m)}*K

  • 其中 K=0,1,...,gcd(a,m)-1，x 是 ax+my=c 的一个解。

例题：同余式方程

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <cstring>
#include <iostream>
#include <utility>
#include <map>
#include <algorithm>
#include <vector>
#include <climits>
#include <string>
#include <ctime>
#include <cmath>
#include <sstream>
using namespace std;

//求解最大公约数函数(递归算法)
int gcd(int a,int b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}

//扩展欧几里得算法
int exGcd(int a,int b,int &x,int &y)//x和y使用引用
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	int g = exGcd(b,a%b,x,y);//递归计算exGcd(b,a%b,x,y)
	int temp = x;//存放x的值
	x=y;//更新x=y(old)
	y=temp-a/b*y;//更新y=x(old)-a/b*y(old)
	return g;//g是gcd
}

//主函数
int main()
{
    int a,c,m;
    scanf("%d %d %d",&a,&c,&m);
    if(c%gcd(a,m)==0)
    {
        int x,y,g;
        g=exGcd(a,m,x,y);
        int x_ans;
        //分m/g的正负
        if(m/g<0)
            x_ans=((x*c/g)%(m/g)-m/g)%(m/g);
        else
            x_ans=((x*c/g)%(m/g)+m/g)%(m/g);
        printf("%d\n",x_ans);
    }
    else
        printf("No Solution\n");
    system("pause");// 防止运行后自动退出，需头文件stdlib.h
    return 0;
}
  • 总结：这道题目需要注意 m/g 是否为负数，其余部分上述介绍的思路一致，属于简单题。

逆元求解以及 (b/a)%m 的计算

  • 接着解决最后一个问题，假设 a、m 是整数，求 a 模 m 的逆元。
  • 先解释什么是逆元（此处特指乘法逆元）：
  • 假设 a、b、m 是整数，m＞1，且有 ab≡1(mod m)ab\equiv 1(mod \ m) 成立，那么就说 a 和 b 互为模 m 的逆元，一般也记作 a≡1b(mod m)a\equiv \frac{1}{b}(mod \ m) 或 b≡1a(mod m)b\equiv \frac{1}{a}(mod \ m)。
  • 通俗地说，如果两个整数的乘积模 m 后等于 1，就称它们互为逆元。
  • 那么逆元有什么用处呢？
  • 对于乘法来说有 (b×a)%m=((b%m)×(a%m))%m(b×a) \% m = ((b \% m)×(a \% m))\% m 成立。
  • 但是对除法来说 (b÷a)%m=((b%m)÷(a%m))%m(b÷a) \% m = ((b \% m)÷(a \% m))\% m 却不成立；
  • 同时 (b÷a)%m=((b%m)÷a)%m(b÷a) \% m = ((b \% m)÷a)\% m 也不成立。
  • 例如，如果要对 12÷4 对 2 取模，采用 ((12%2)÷4)%2((12 \% 2)÷4)\% 2 的做法会得到错误的结果 0，而实际上应当是 1。这时就需要逆元来计算 (b÷a)%m(b÷a)\% m。
  • 通过找到 a 模 m 的逆元 x, 就有 (b÷a)%m=(b×x)%m(b÷a) \% m = (b×x) \% m 成立（只考虑整数取模，也即假设 b%a=0，即 b 是 a 的整数倍），于是就把除法取模转化为乘法取模，这对于解决除数 b 非常大（使得 b 已经取过模，不是原始值）的问题来说是非常实用的。
  • 由定义知，求 a 模 m 的逆元，就是求解同余式 ax≡1(mod m)ax\equiv 1(mod \ m)，并且在实际使用中，一般把 x 的最小正整数称为 a 模 m 的逆元，因此下文提到的逆元都是默认为 x 的最小正整数解。
  • 显然，同余式 ax≡1(mod m)ax\equiv 1(mod \ m) 是否有解取决于 1%gcd(a,m) 是否为 0，而这等价于 gcd(a,m) 是否为 1：
  1. 如果 gcd(a,m)≠1，那么同余式 ax≡1(mod m)ax\equiv 1(mod \ m) 无解，a 不存在模 m 的逆元。
  2. 如果 gcd(a,m)=1，那么同余式 ax≡1(mod m)ax\equiv 1(mod \ m) 在 (0,m) 上有唯一解，可以通过求解 ax+my=1ax+my=1 得到。
  • 注意：由于 gcd(a,m)=1，因此 ax+my=1=gcd(a,m)，直接使用扩展欧几里得算法解出 x 之后就可以用 (x%m+m)%m 得到在 (0,m) 范围内的解，也就是所需要的逆元。
数据结构
#数据结构 #算法
算法笔记之基础篇
http://example.com/2023/11/05/algorithm2/
作者
Mr.CHUI
发布于
2023年11月5日
许可协议